全局比对&Needleman-Wunsch算法 | 生物人最值得看的哈佛生信课03

另一篇有关局部比对的文章

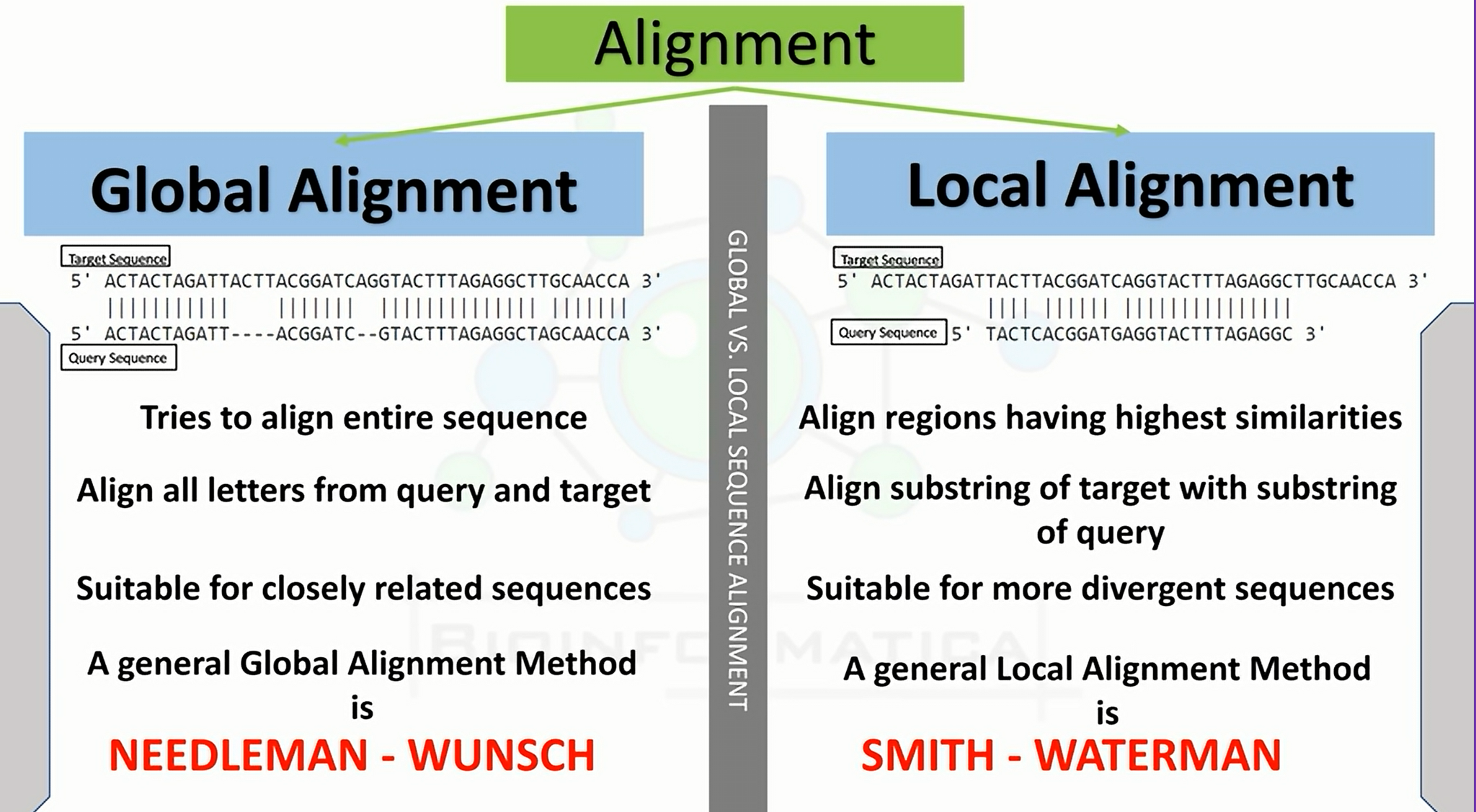
全局比对（Global aliment）

全局比对是指将参与比对的两条序列里面的所有字符进行比对。全局比对在全局范围内对两条序列进行比对打分，找出最佳比对，主要被用来寻找关系密切的序列。其可以用来鉴别或证明新序列与已知序列家族的同源性，是进行分子进化分析的重要前提。其代表是Needleman-Wunsch算法。

from：https://zhuanlan.zhihu.com/p/150579075

from：12.global sequence alignment & needleman-wunsch __ algorithm and example_哔哩哔哩_bilibili

Needleman-Wunsch算法步骤

和上次的local aliment部分类似：

在动态规划算法中，解题思路往往是把一个问题分解成更小更简单的子问题，通过解决子问题，来得到原问题的解。

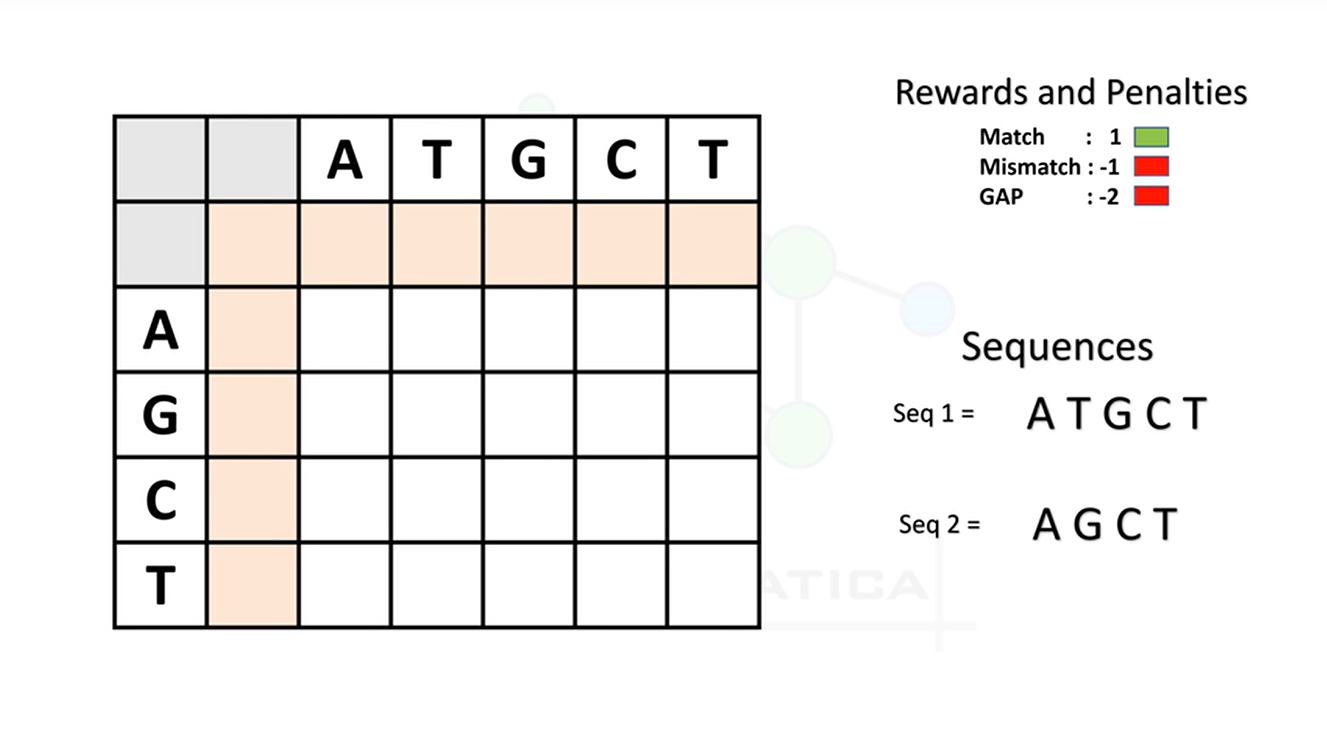
1. **初始化：**创建一个矩阵，其大小为序列A和序列B的长度加1。这个矩阵用于存储比对分数。
   

2. 得分规则：定义匹配match得分（通常为+1），错配mismatch得分（通常为-1）和空位罚分gap（通常为-2）。

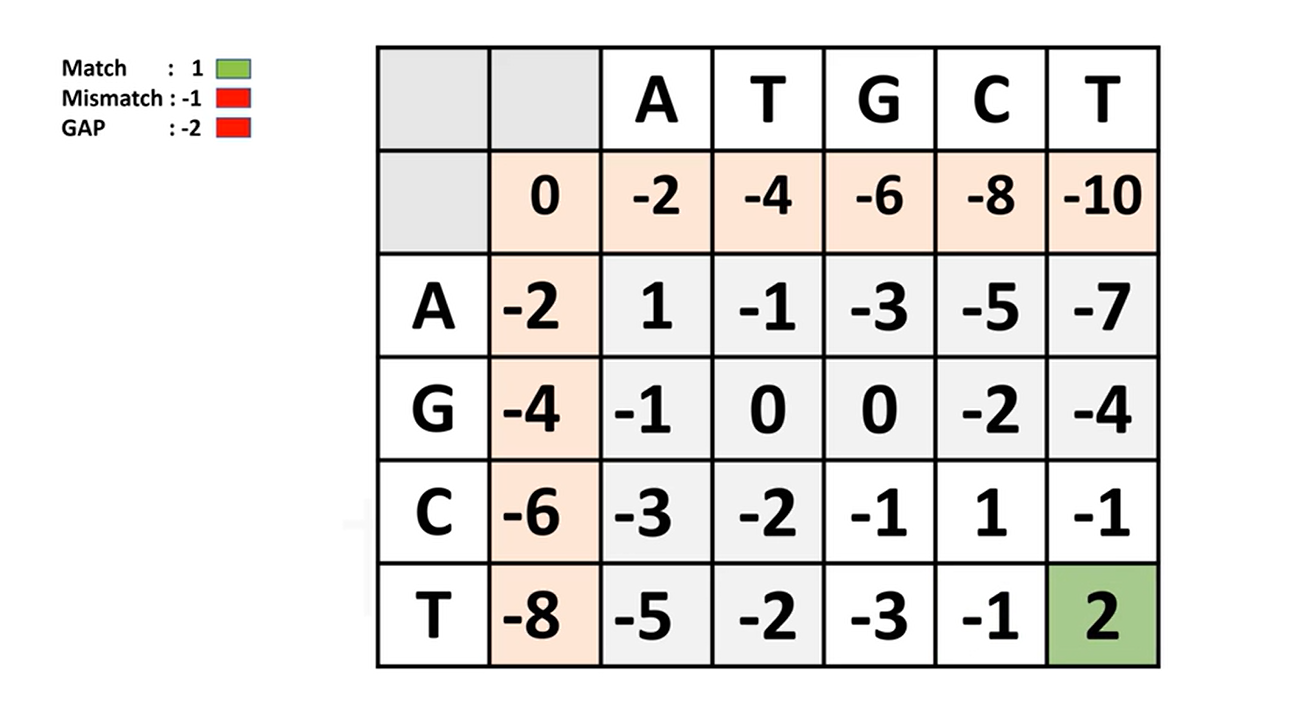
3. 填充矩阵：矩阵的左上角开始，逐个填充矩阵的每个格子。填充的规则如下：

• 如果当前比较的两个字符相同，则得分通常是正数（例如+1）。
• 如果字符不同，则得分通常是负数或零（例如-1或0）。
• 每个格子的得分是以下三个值中的最大值：
  • 左边格子的得分减去空位罚分（代表在序列B中插入一个空格）。
  • 上边格子的得分减去空位罚分（代表在序列A中插入一个空格）。
  • 左上角格子的得分加上匹配得分（如果字符相同）或错配得分（如果字符不同）。
• **计算出的得分是负数，则保留该负数，因为全局比对要求整个序列对齐，不关心得分为负。**这里是和local alignment不同的地方
  

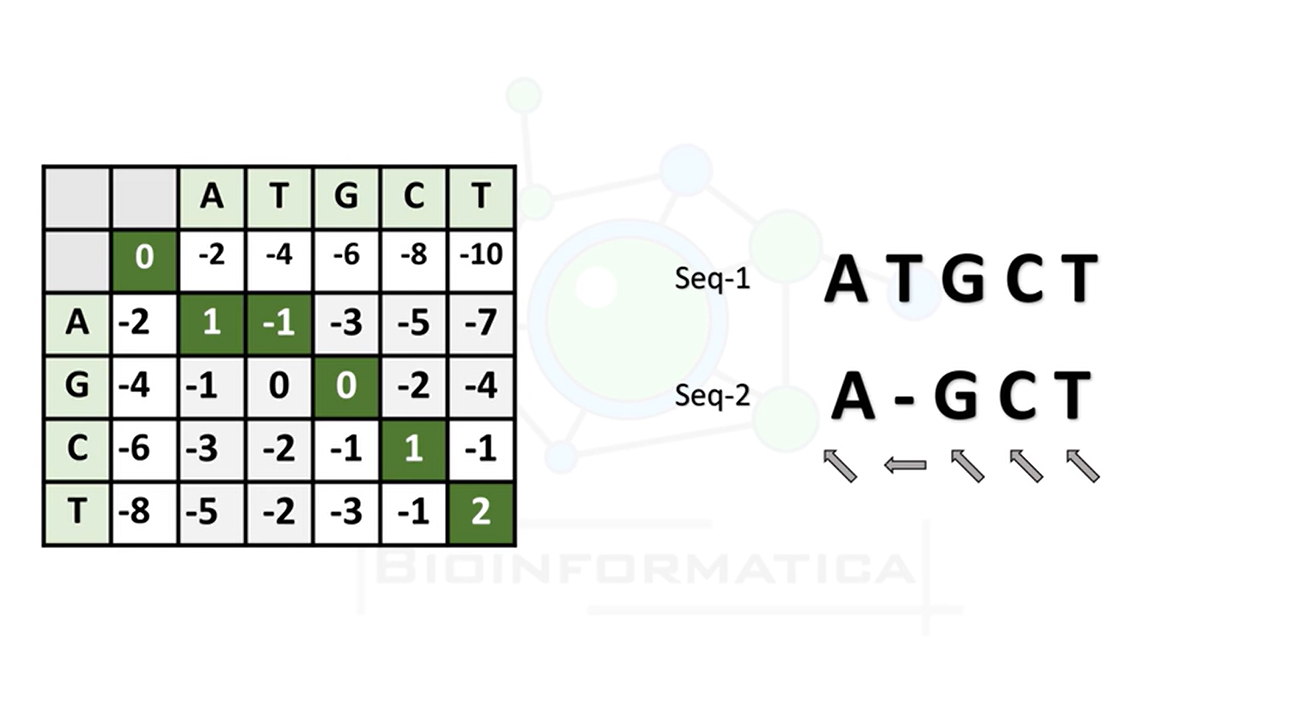
1. 追踪回溯（Traceback）：

• 如果当前格子的得分来自于左上角的格子（即两个字符进行了匹配或错配），则：

• 如果两个字符相同，将它们配对，并移动到左上角的格子。

• 如果两个字符不同，也将它们配对（错配），并移动到左上角的格子。

• 如果当前格子的得分来自于左边的格子，则：

• 在序列B中添加一个空位（gap），并移动到左边的格子。

• 如果当前格子的得分来自于上边的格子，则：
  在序列A中添加一个空位（gap），并移动到上边的格子。