WPA中RC4的新型线性相关性

原创于 2025-10-19 12:46:30 发布 · 295 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#RC4 #WPA #线性相关性

WPA中利用IV的RC4 PRGA状态信息相关的新线性相关性

摘要

RC4是由罗恩·里维斯特于1987年设计的一种流密码，广泛应用于各种场景。WPA是这些应用之一，其中使用TKIP作为密钥生成过程以避免WEP产生的弱IV。在FSE 2014上，Sen Gupta 等人和帕特森等人提出了两种针对WPA的不同攻击。两者都关注WPA中密钥流字节与RC4密钥前3个字节之间的相关性。本文中，我们关注通用RC4和WPA中内部状态与RC4密钥前3个字节之间的线性相关性，其中WPA中的RC4密钥前3个字节为 known。结果，我们发现了多种新的线性相关性，并从理论上证明了这些相关性。

关键词： RC4 · WPA · Linear相关性

1 引言

RC4 是由罗恩·里维斯特于 1987年设计的一种流密码，广泛应用于安全套接层/ 传输层安全（SSL/TLS）、有线等效保密（WEP）和 Wi‐Fi保护访问（ WPA）等各种应用中。由于其广泛使用和结构简单，自 1994 年其技术规范在互联网上公开以来，RC4 一直成为热门的密码分析目标。

WEP 是一种用于 IEEE 802.11 无线网络的安全协议，于 1999 年标准化。然而，自 [7,16,17]弗卢尔等人在 2001[3],展示了 WEP 中一类弱 IV 之后，已提出了多种针对 WEP 的攻击，如今 WEP 被认为已完全被攻破。为了避免弗卢尔等人的攻击，[3],WEP 已于 2003年被 WPA 取代。WPA 改进了密钥调度过程，称为临时密钥完整性协议（TKIP），以避免生成 WEP 中的一类弱 IV。

TKIP 的一个显著特征是 RC4 密钥的前 3 个字节 K[0]、 K[1]和 K[2]是从 IV 派生而来的，因此它们是公开的。 K[1]的取值范围被限制为 [32, 63]或 [96, 127]，以避免弗卢尔等人提出的已知 WEP 攻击。[3]。

2 预备知识

2.1 RC4描述

本文使用以下符号表示。

K, l：密钥，密钥长度（字节）
r：轮数
N：状态中的数组数量（通常为 N= 256）
SrK：第 r轮交换后 KSA 的状态
Sr：第 r轮交换后 PRGA 的状态
i, j K r：第 r轮 SrK 的索引
ir, jr：第 r轮 Sr 的索引
Zr：第 r轮的一个输出密钥流
tr： Zr 的索引

RC4 由两个算法组成：密钥调度算法（KSA）和伪随机生成算法（PRGA）。KSA 使用长度为 SNK字节的密钥 K生成状态 l，如算法1所述。然后， KSA 中的最终状态 SNK作为 PRGA 的输入，即 S0。一旦状态 S0被计算出来，PRGA 在每一轮中生成一个密钥流字节 Zr，如算法2所述。该密钥流字节 Zr将与明文进行异或以生成密文。

算法1. KSA

1: for i= 0到 N −1 do
2: SK 0[i] ← i
3: 结束循环
4: j K 0 ← 0
5: for i= 0到 N −1 do
6: j K i+1 ← j K i[i]+ K[i mod l]
7: 交换(SK i[i], SK i[j K i+1])
8: 结束循环

算法2. PRGA

1: r ← 0, i0 ← 0, j0 ← 0
循环
3: r ← r+1, ir ← ir−1+1
4: jr ← jr−1+ Sr−1[ir]
5: 交换(Sr−1[ir], Sr−1[jr])
6: tr ← Sr[ir]+ Sr[jr]
7: Zr ← Sr[tr]
8: 结束循环

2.2 WPA描述

为了生成一个16字节的RC4密钥，WPA使用了两个密钥调度过程：一个密钥管理方案和包含临时密钥的TKIP密钥哈希函数 [5]用于生成RC4密钥和消息完整性校验码函数以确保消息的完整性。基于IEEE 802.1X认证后的密钥管理方案生成一个16字节的临时密钥（TK）。然后，将TK、一个6字节的发送方地址和一个48位的IV（即序列计数器）作为输入提供给临时密钥哈希函数。该临时密钥哈希函数生成RC4密钥的最后13字节。剩余的RC4密钥，即前3字节，通过IV的最后16位（IV16）按如下方式计算：

K[0]=(IV16>> 8)& 0xFF,
K[1]=((IV16>> 8) \| 0x20)& 0x7F,
K[2]= IV16& 0xFF.

为了避开弗卢尔等人提出的已知WEP攻击 [3]， K[1] 的取值范围被限制在 [32, 63] 或 [96, 127] 之内。

3 以往工作

1995年，Roos偏差[15], RC4密钥字节与PRGA初始状态之间的相关性 S0在[14]中被证明，具体如下：

命题1. [14,推论 2]。 在 0 ≤ y ≤N −1的PRGA初始状态中，我们有

Pr(S0[y]= y(y+ 1) 2 + y ∑ x=0 K[x]) ≈(1 − y N) ·(1 − 1 N)[ y(y +1) 2 +N] + 1 N .

在FSE 2008上，Maitra和Paul展示了类似于Roos偏差的相关性[9],即所谓的嵌套 Roos偏差，见于[10]。嵌套Roos偏差具体如下：

命题2. [9,定理 2]。 在 0 ≤ y ≤ 31的PRGA初始状态中，Pr(S0[S0[y]]= fy) 约为

(y N + 1 N(1 − 1 N) 2−y +(1 − y N) 2 (1 − 1 N))(1 − 1 N) y ( y +1 ) 2 +2N−4 ,

其中 fy = y(y +1) 2 +∑ y x=0 K[x]。

在 FSE 2014 中，Sen Gupta 等人表明， K[0]+ K[1]的分布由于 WPA 中由临时密钥哈希函数生成的 K[0]和 K[1]之间的关系而存在偏差[4]。该分布如下所示：

命题3. [4,定理 1]。 对于 0 ≤ v ≤ N − 1，由WPA中的临时密钥哈希函数生成的 K[0]和 K[1]之和 v的分布如下所示：

Pr(K[0]+ K[1]= v)= 0当v为奇数时，
Pr(K[0]+ K[1]= v)= 0当v为偶数且v ∈[0, 31] ∪[128, 159]时，
Pr(K[0]+ K[1]= v)= 2/256当v为偶数且 v ∈[32, 63] ∪[96, 127] ∪[160, 191] ∪[224, 255]时，
Pr(K[0]+ K[1]= v)= 4/256当v为偶数且v ∈[64, 95] ∪[192, 223].时

他们还表明，命题3结合命题1中显示的Roos偏差，会在PRGA初始状态的分布上引发一种特征性偏差 S0[1]，这种偏差深刻影响了第一个密钥流字节的偏差 Z1等。

4 新的线性相关性

4.1 实验观察

让我们研究四个未知值Sr[ir+1]、 Sr[jr+1]、jr+1和 tr+1在 r ≥ 0下的新相关性。其他密钥流字节的线性相关性在[4]中进行了研究。令 Xr ∈{Sr[ir+1], Sr[jr+1], jr+1, tr+1}、 a, b, c, d ∈{0,±1}和 e ∈{0,±1,±2,±3}，

Xr= a·Zr+1+ b·K[0]+ c·K[1]+ d·K[2]+ e. (1)

这些由公式(1)引起的偏差可加入到WPA中已知密钥下的Sr[ir+1],Sr[jr+1], jr+1和 tr+1的已知偏差集合中 r ≥ 0，例如 K[0], K[1]和 K[2]，这可能会降低针对RC4[2,8,12]的现有状态恢复攻击的计算复杂度，尤其是在WPA中。

我们已经检查了在每一轮中由公式(1)定义的全部 4 · 34 · 7方程，使用了 232组随机生成的16字节密钥，分别应用于通用RC4和WPA。一些显著的实验结果列于表1和3中。由于篇幅限制，仅列出在通用RC4或WPA中相关性大于 0.0048或小于0.0020的结果。我们强调，在WPA中 S0[i1]= K[0]的情况成为不可能条件（概率为0），因此， S0[i1]的取值范围从[0, N−1]{K[0]}开始变化。

我们的动机是理论上证明表1中所示的这些线性相关性。

为了证明以下定理，我们经常使用Roos偏差（命题1）、嵌套Roos偏差（命题2）以及 K[0]+K[1]=v的概率（命题3），它们分别记为 α y = Pr( S0[y]= y(y +1) 2 +∑ y x=0 K[x])，β y = Pr(S0[S0[y]]= y(y +1) 2 +∑ y x=0 K[x]) 和 γv= Pr(K[0]+ K[1]= v)。根据RC4流密码的均匀随机性，我们假设

示意图0 的观察结果)

我们通过实验确认某些事件（例如状态信息）不存在显著偏差的概率为 1 N由于证明中的随机关联所致。此外，我们假设在通用RC4中RC4密钥是均匀随机生成的。

4.2 通用RC4和WPA中 S0[i1]的偏差

在本节中，我们证明了定理1–4。定理1和2表明，在通用RC4和WPA中， S0[i1]=K[0]成立的概率很低且为0。定理3和4表明，在WPA中，S0[i1]= K[0]−K[1]−3和 K[0]−K[1]−1的发生频率是概率 1 N 的两倍，这是由于随机关联所致。定理3还表明，事件(S0[i1]= K[0]−K[1]−3)在通用RC4中提供了具有正向偏差的一个案例。

定理1. 在PRGA的初始状态中，我们有

Pr(S0[i1]= K[0])RC4 ≈ 1 N(1 − 1 N) N−2 .

证明。 图2展示了KSA的前两轮中的状态转移图。从算法 1的步骤6，两者 j K 1 = j K 0 + S K

示意图1

且 jK 2= jK 1+ SK 1[1]+ K[1]= K[0]+ K[1]+ SK 1[1]成立。事件(S0[i1]= K[0])的概率可分解为三条路径： K[0]+ K[1]= 0（路径1）、 K[0]+ K[1]= 255（路径2）和 K[0]+ K[1] = 0, 255（路径3）。路径1和路径2均进一步分为两个子路径： K[0]= 1（路径1‐1和路径2‐1）以及K[0] = 1（路径1‐2和路径2‐2）。在以下的证明中，为简便起见，我们使用 S0[1]代替 S0 i1 ，并用 SNK[1]表示。

路径1‐1. 图3显示了路径1‐1中的状态转移图。在KSA的第二轮之后，SK 2[1]= K[0]始终成立，因为 j K 1= K[0]= 1且 j K 2= K[0]+ K[1]+ SK 1[1]= 0+ 0= 0。此外， SrK[1]= SK 2[1]对于 3 ≤ r ≤ N，如果在接下来的 N −2轮中发生 j K r = 1，其概率约为 (1 − 1 N)N−2。因此，路径1‐1中的概率如下所示：

Pr(S0[1]= K[0] \| Path 1-1) ≈(1 − 1 N)N−2.

路径1‐2. 图4显示了路径1‐2中的状态转移图。 SK 2[0]= K[0]始终成立，因为 jK 1= K[0] = 1且 jK 2=（K[0]+K[1]）+SK 1[1]= 0+1= 1。然后，事件（S0[1]= K[0]）从不发生，因为 SrK[1] = K[0]对于 r ≥ 2始终成立。因此，路径1‐2中的概率为0。

路径2‐1. 图5显示了路径2‐1中的状态转移图。 SK 2[0]= K[0]始终以与路径1‐2相同的方式成立。然后，事件（S0[1]= K[0]）从不发生，因为 SrK[1] = K[0]对于 r ≥ 2始终成立。因此，路径2‐1中的概率为0。

路径2‐2. 图6显示了路径2‐2中的状态转移图。 SK 2[1]= K[0]始终以与路径1‐1相同的方式成立。然后，当 Sr[1]= SK 2[1]对于 3 ≤ r ≤ N时，事件（ S0[1]= K[0]）发生。因此，路径2‐2中的概率如下所示：

Pr(S0[1]= K[0] \| Path 2-2) ≈(1 − 1 N) N−2 .

路径3. 图2显示了路径3中的状态转移图。 SK 2[0]= K[0]始终以与路径1‐2和路径2‐1相同的方式成立。然后，事件（S0[1]=K[0]）从不发生。因此，路径3中的概率为0。

总之，事件 (S0[i1]= K[0]) 仅在路径1‐1或2‐2中发生。因此，我们得到

Pr(S0[i1]= K[0])= Pr(S0[i1]= K[0] \| Path 1-1)· Pr(Path 1-1) + Pr(S0[i1]= K[0] \| Path 2-2)· Pr(Path 2-2)
≈(1 − 1 N) N−2 · 1 N2 +(1 − 1 N) N−2 · 1 N(1 − 1 N)= 1 1 N) N−2 .

定理2. 在WPA中PRGA的初始状态中，我们有

Pr(S0[i1]= K[0])WPA= 0.

示意图2

示意图3

示意图4

证明. 注意事件（S0[1]= K[0]）发生当且仅当 K[0]+K[1]= 0或255，而命题3表明在 WPA中 K[0]+ K[1]= 0和255均不成立。因此，事件（S0[1]= K[0]）在WPA中的概率为0。

定理3. 在PRGA的初始状态中，我们有

Pr(S0[i1]= K[0] − K[1] −3) ≈
⎧ ⎪⎪⎨ ⎪⎪⎩
2 N α1+ 1 N(1 − 2 N)(1 − α1) for RC4,
4 N α1+ 1 N(1 − 4 N)(1 − α1) for WPA.

证明。 事件(S0[i1]= K[0] − K[1] −3)的概率可以分解为两条路径： K[1]= 126，254 （路径1）和 K[1] = 126，254（路径2）。在以下的证明中，为了简化，我们使用 S 0[1]代替 S 0 i1 。

路径1在 K[1]= 126，254时，事件(S0[1]= K[0]−K[1]−3)发生当且仅当 S0[1]= K[0]+ K[1]+ 1。因此，路径1中的概率如下所示：

Pr(S0[1]= K[0] − K[1] −3 \| Path 1)= α1.

路径2. 在 K[1] = 126,254，事件（S0[1]= K[0] − K[1] − 3）从不发生，如果 S0[1]= K[0]+K[1]+1。如果 S0[1] = K[0]+K[1]+1成立，则我们假设事件（ S0[1]= K[0] − K[1] − 3）由于随机关联以概率 1 N发生。因此，路径2中的概率如下所示：

Pr(S0[1]= K[0] − K[1] −3 \| Path 2) ≈ 1 N ·(1 − α1).

综上所述，我们得到

Pr(S0[i1]= K[0] − K[1] −3) = Pr(S0[1]= K[0] − K[1] −3 \| Path 1)· Pr(Path 1) + Pr(S0[1]= K[0] − K[1] −3 \| Path 2)· Pr(Path 2)
≈
⎧⎪⎪⎨ ⎪⎪⎩
2 N α1+ 1 N)(1 − α1) for RC4,
4 N α1+ 1 N(1 − 4 N)(1 − α1) for WPA,

其中 α1= Pr(S0[1]= K[0]+ K[1]+ 1) ≈(N−1 N)N+2+ 1 N。在通用RC4中， K[1]= 126或 254 的概率为 N1，以便均匀随机生成。另一方面，在WPA中， K[1]= 126或 254 的概率分别为 4 N或 0。因此，定理 3反映了通用RC4和WPA中 Pr(K[1]= 126,254) 的差异。

定理4。 在PRGA的初始状态中，我们有

Pr(S0[i1]= K[0] − K[1] −1)
≈
⎧⎪⎪⎨ ⎪⎪⎩
1 N)α1+ 1 N(1 − 2 N)(1 − α1) for RC4,
4 N α1+ 1 N(1 − 4 N)(1 − α1) for WPA.

证明。 事件(S0[i1]= K[0] − K[1] −1)的概率可以分解为三条路径： K[1]= 127（路径1）、 K[1]= 255（路径2）和 K[1] = 127,255（路径3）。在接下来的证明中，为了简化，我们使用 S0[1]代替 S0 i1 。

路径1 在 K[1]= 127中，事件(S0[1]= K[0] − K[1] − 1)发生当且仅当 S0[1]= K[0]+ K[1]+ 1。因此，路径1中的概率如下所示：

Pr(S0[1]= K[0] − K[1] −1 \| Path 1)= α1.

路径2。 在 K[1]= 255中，事件（S0[1]= K[0] − K[1] − 1）发生当且仅当 S0[1]= K[0]+K[1]+1，且 K[0]+K[1]+1= K[0]−K[1]−1= K[0]。因此，根据定理 1中的讨论，事件（S0[1]= K[0]）发生当且仅当（K[0]+ K[1]= 0 ∧ K[0]= 1）或（ K[0]+ K[1]= 255 ∧ K[0] = 1）成立。于是，在假设 K[1]= 255和 S0[1]= K[0]+ K[1]+ 1均成立的情况下，事件（S0[1]= K[0] − K[1] −1）发生当且仅当 K[0]= 0或 1 成立。因此，路径2的概率如下所示： Pr(S0[1]= K[0] − K[1] −1 | Path 2) ≈ Pr(K[0]= 0, 1)· α1.

路径3. 在 K[1] = 127,255，事件（S0[1]= K[0] − K[1] − 1）从不发生，如果 S0[1]= K[0]+K[1]+1。如果 S0[1] = K[0]+K[1]+1成立，则我们假设事件（ S0[1]= K[0] − K[1] − 1）由于随机关联以概率 1 N发生。因此，路径3中的概率如下所示：

Pr(S0[1]= K[0] − K[1] −1 \| Path 3) ≈ 1 N ·(1 − α1).

综上所述，我们得到 Pr(S0[i1]= K[0] − K[1] −1) = Pr(S0[i1]= K[0] − K[1] −1 | Path 1)· Pr(Path 1) + Pr(S0[i1]= K[0] − K[1] −1 | Path 2)· Pr(Path 2) + Pr(S0[i1]= K[0] − K[1] −1 | Path 3)· Pr(Path 3)

≈
⎧⎪⎪⎨ ⎪⎪⎩
1 N)α1+ 1 N(1 − 2 N)(1 − α1) for RC4,
4 N α1+ 1 N(1 − 4 N)(1 − α1) for WPA,

其中 α1= Pr(S0[1]= K[0]+ K[1]+ 1) ≈(N−1 N) N+2+ 1 N。对于WPA，定理 3和4表明Pr(S0[i1]= K[0]−K[1]−3)= Pr(S0[i1]=K[0] − K[1] −1) 成立。这是因为在WPA中， K[1]= 127或255的概率分别为 4 N或0。

4.3 通用RC4和WPA中S255[i256]的偏差

定理 5表明，在通用RC4和WPA中，S255[i256]= K[0]均以高概率成立。另一方面，定理 6表明， S255[i256]= K[1]仅在WPA中以高概率成立。

定理5. 在PRGA的255轮之后，我们有

Pr(S255[i256]= K[0]) ≈ α0(1 − 1 N) 255 + 1 N(1 − α0)(1 −(1 − 1 N) 255 ).

证明. 事件(S255[i256]= K[0])的概率可以分解为两条路径： S 0[0]= K 0 和 S 0[0] = K 0 。在接下来的证明中，为了简化，我们使用 S 255[0]代替 S 255[i256] (i256 = 0)。

路径1。 在 S0[0]= K[0]中，如果 Sr[0]= S0[0]对于1 ≤ r ≤ 255发生 S255[0]= K[0]事件，则该事件发生的概率约为(1 − 1 N)255。因此，路径1的概率如下所示：

Pr(S255[0]= K[0] \| Path 1) ≈(1 − 1 N)255 .

路径2。 在 S0[0] = K[0]中，如果 Sr[0]= S0[0]对于 1 ≤ r ≤ 255成立，则事件( S255[0]= K[0])永远不会发生。除了当Sr[0]= S0[0]对于 1 ≤ r ≤ 255成立时，其概率约为(1 −(1 − 1 N)255)，我们假设由于随机关联，事件(S255[0]= K[0])以概率 1 N发生。因此，路径2中的概率如下所示：

Pr(S255[0]= K[0] \| Path 2) ≈ 1 N(1 −(1 − 1 N)255).

总之，我们得到

Pr(S255[i256]= K[0])= Pr(S255[i256]= K[0] \| Path 1)· Pr(Path 1) + Pr(S255[i256]= K[0] \| Path 2)· Pr(Path 2)
≈ α0(1 − 1 N)255 + 1 N(1 − α0)(1 −(1 − 1 N)255),

其中 α0= Pr(S0[0]= K[0]) ≈(1 − 1 N)N+ 1 N。

在展示定理6之前，我们将在引理1中说明S0[0]= K[1]在WPA中具有高概率。

引理1。 在PRGA的初始状态中，我们有

Pr(S0[0]= K[1]) ≈
⎧⎪⎪⎨ ⎪⎪⎩
1 N − 1 N2( 1 − α0) for RC4,
1 4( 3 N +(1 − 3 N)α0) for WPA.

证明. 事件(S0[0]= K[1])的概率可以分解为两条路径：K[1]= K[0]（路径1）和 K[1] = K[0]（路径2）。

路径1. 在 K[1]= K[0]中，事件（S0[0]= K[1]）发生的充要条件是 S0[0]= K[0]。因此，路径1中的概率如下所示：

Pr(S0[0]= K[1] \| Path 1)= α0.

路径2。 在 K[1] = K[0]中，如果 S0[0]= K[0]，则事件(S0[0]= K[1])永远不会发生。如果 S0[0] = K[0]，则我们假设事件(S0[0]= K[1])由于随机关联以概率 1 N 发生。因此，路径2中的概率如下所示：

Pr(S0[0]= K[1] \| Path 2) ≈ 1 N ·(1 − α0).

总之，我们得到

Pr(S0[0]= K[1])= Pr(S0[0]= K[1] \| Path 1)· Pr(Path 1) + Pr(S0[0]= K[1] \| Path 2)· Pr(Path 2)
≈
⎧⎪⎪⎨ ⎪⎪⎩
α0 · 1 N+ 1 N(1 − α0)·(1 − 1 N)= 1 N − 1 N2(1 − α0) for RC4,
α0 · 1 4+ 1 4= 1 4( 3 N)α0) for WPA,

其中 α0= Pr(S0[0]= K[0]) ≈(1 − 1 N)N+ 1 N。

引理 1反映了事件（K[1]= K[0]）在WPA中的概率 1 4,高于通用RC4中的概率 1 定N理。6。在PRGA的第255轮之后，我们有

Pr(S255[i256]= K[1]) ≈ δ(1 − 1 N)255 + 1 N(1 − δ)(1 −(1 − 1 N)255),

其中 δ是 Pr(S0[0]= K[1])，如引理 1所述。

证明。 该证明本身与定理 5 类似，且使用了引理 1中给出的事件(S0[0]= K[1])的概率，而不是事件(S0[0]=K[0])的概率。因此，我们得到

Pr(S255[i256]= K[1])= Pr(S255[0]= K[1] \| S0[0]= K[1])· Pr(S0[0]= K[1]) + Pr(S255[0]= K[1] \| S0[0] = K[1])· Pr(S0[0] = K[1])
≈ δ(1 − 1 N)255 + 1 N(1 − δ)(1 −(1 − 1 N)255),

其中 δ是引理1中给出的S0[0]= K[1]的概率。

WPA中利用IV的RC4 PRGA状态信息相关的新线性相关性

4 新的线性相关性

4.4 通用RC4和WPA中Sr ir+1 的偏差

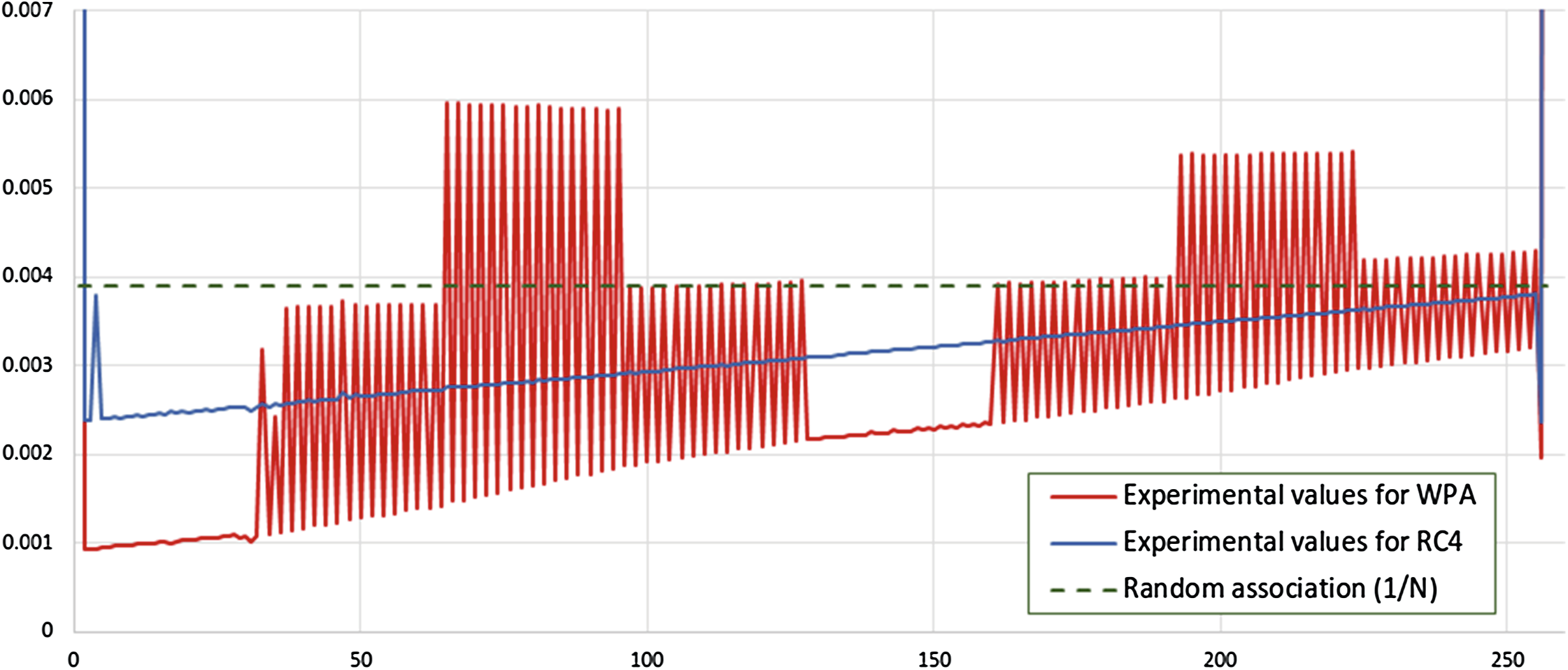
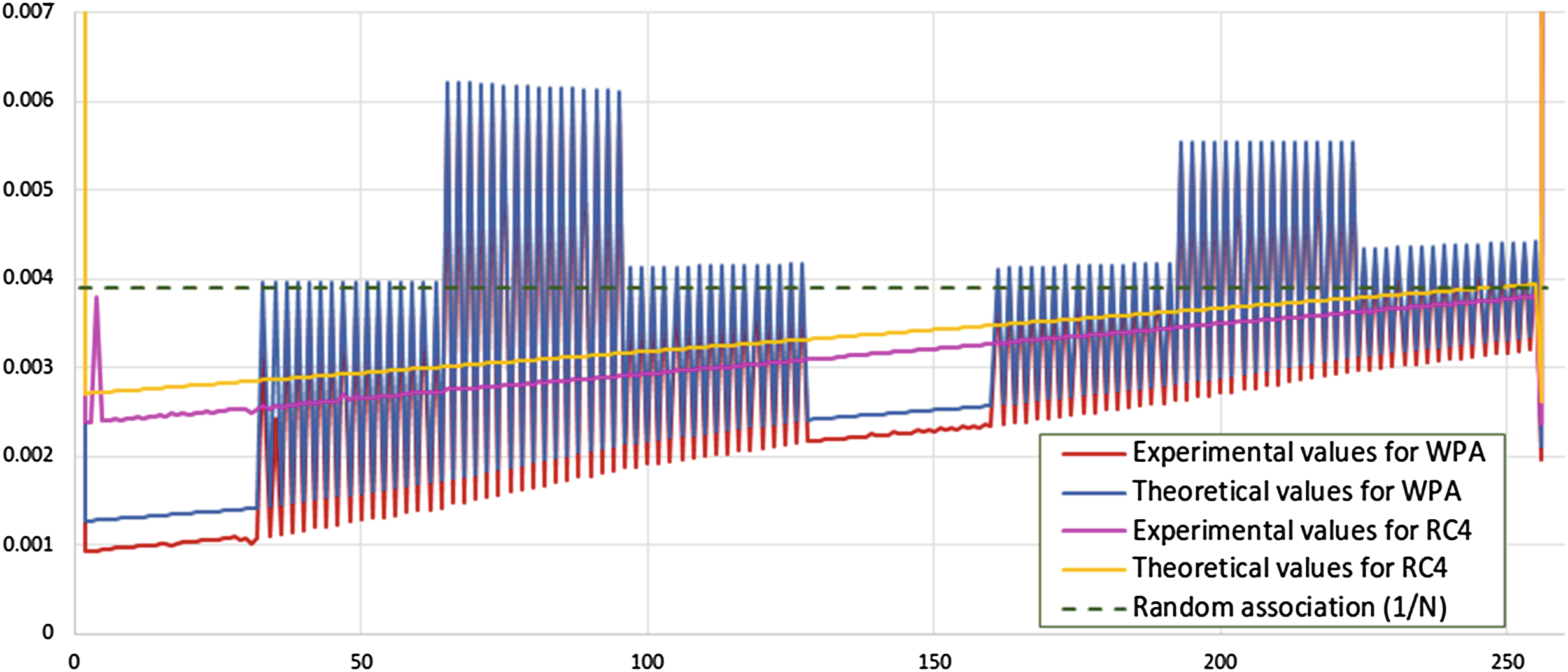
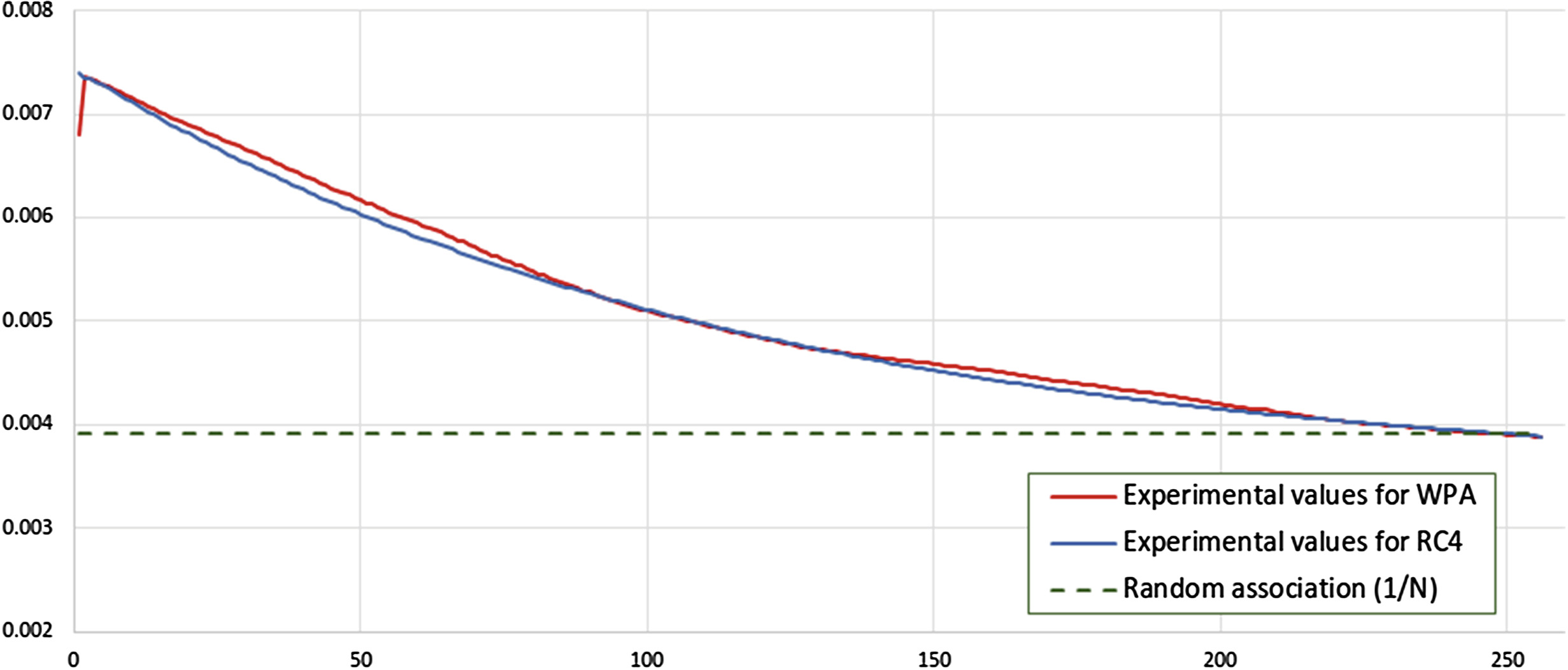
定理 7给出了 Sr[ir+1]= K[0]+ K[1]+ 1) 在 0 ≤ r ≤ N 时的概率，其实验结果列于第 1节4.1的图7中。在证明定理7之前，先证明引理2和3，即PRGA前两轮状态的分布。

引理2. 在 0 ≤ x ≤ N −1的PRGA初始状态中，我们有

Pr(S0[x]= K[0]+ K[1]+ 1)
≈
⎧ ⎪⎪⎪⎪⎪⎪⎪⎨ ⎪⎪⎪⎪⎪⎪⎪⎩
(1 − 1 N) N+2 + 1 N if x=1
1 N2( 1 − 1 N) 2 if x=0 for WPA
1 N(1 − 1 N(1 − x+ 1 N)+(1 − 1 N) N−x−2 ) otherwise.

证明. 首先，事件（S0[1]= K[0]+ K[1]+1）的概率遵循命题1中的结果，即，

Pr(S0[1]= K[0]+ K[1]+ 1) ≈(1 − 1 N)N+2+ 1 N。

接下来，事件(S0[x]= K[0]+ K[1]+ 1)在 x ∈[0, N]{1}下的概率可以分解为两条路径： SxK[jxK+1]= K[0]+ K[1]+ 1（路径1）和SxK[jxK+1] = K[0]+ K[1]+ 1（路径2）。

路径1。 由于交换操作， SxK[jxK+1]= K[0]+ K[1]+1, SxK+1[x]= K[0]+ K[1]+1始终成立。此外，如果 SrK[x]= SxK+1[x]对于 x+ 2 ≤ r ≤ N成立，其概率约为(1 − 1 N)N−x−1，则 S0[x]= K[0]+K[1]+ 1始终成立。因此，路径1中的概率如下所示：

Pr(S0[x]= K[0]+ K[1]+ 1 \| Path 1) ≈(1 − 1 N)N−x−1.

路径 2 SxK[jxK+1] = K[0]+K[1]+1
y SxK[y]= K[0]+ K[1]+ 1
SxK+1[x]= K[0]+K[1]+1

假设成立。在中，由于交换操作，从不成立。在第 x+ 1轮之后，若 x ≥ y，则事件（S0[x] = K[0]+ K[1]+ 1）发生，因为 SrK[x] = K[0]+K[1]+1对于 x+1 ≤ r ≤ N始终成立。否则，如果 x< y，则我们假设事件（ S0[x]= K[0]+ K[1]+ 1）以概率 1 N由于随机关联而发生，且 x< y的概率为 1 − x+1 N 。为了满足 x< y，我们进一步考虑 K[0]= 1，其概率为 1 N。如果 K[0] = 1，则根据定理 1 中的讨论， SK 2[1]= K[0]+ K[1]+ 1始终成立，因此 SrK[x] = K[0]+ K[1]+ 1对 2 ≤ r ≤ N成立。综上所述，路径2中的概率如下所示：

Pr(S0[x]= K[0]+ K[1]+ 1 \| Path 2)= 1 N2(1 − x+ 1 N).

总之，我们得到

Pr(S0[x]= K[0]+ K[1]+ 1) = Pr(S0[x]= K[0]+ K[1]+ 1 \| Path 1)· Pr(Path 1) + Pr(S0[x]= K[0]+ K[1]+ 1 \| Path 2)· Pr(Path 2)
≈ 1 N(1 − 1 N(1 − x+ 1 N)+(1 − 1 N) N−x−2).

在WPA中，当 x= 0时，事件（S0[0]= K[0]+ K[1]+ 1）在 SK 0[j K SK 0[j K S0[0]= K[0]+K[1]+ 1)发生的充要条件是路径2，其概率可简单表示为 1 N2(1 − 1 N) 2。

引理3。 在 0 ≤ x ≤ N −1的PRGA第一轮之后，我们有

Pr(S1[x]= K[0]+ K[1]+ 1)={β1 if x=1
α1γx−1 +(1 − β1)εx otherwise,

其中 εx是 Pr(S0[x]= K[0]+ K[1]+ 1)，如引理 2所述。

证明。 首先，事件（S1[1]= K[0]+ K[1]+1）的概率遵循命题2中的结果，因为根据算法2的第4步和第5步，即 Pr(S1[1]= K[0]+ K[1]+ 1)= β1。

接下来，事件(S1[x]= K[0]+K[1]+1)在 x ∈[0, N−1]{1}下的概率可以分解为两条路径： S0[1]= K[0]+ K[1]+ 1（路径1）和 S0[x]=K[0]+ K[1]+ 1（路径2）。

路径1。 在S0[1]= K[0]+K[1]+1中，如果 j1= x，则由于交换操作，事件( S1[x]= K[0]+K[1]+1)总是发生。尽管 S0[1]= K[0]+ K[1]+1和 j1= x并非相互独立，但通过将 j1= x转换为 j1= S0[1]=K[0]+ K[1]+ 1= x， S0[1]= K[0]+ K[1]+ 1 和 K[0]+K[1]+ 1= x变得相互独立。因此，路径1中的概率如下所示：

Pr(S1[x]= K[0]+ K[1]+ 1 \| Path 1)= Pr(K[0]+ K[1]= x −1).

路径2. 在S0[x]= K[0]+K[1]+1中，如果 j1= x，则由于交换操作，事件( S1[x]= K[0]+K[1]+1)永远不会发生。如果 j1 = x，则 S1[x]= S0[x]= K[0]+ K[1]+ 1始终成立，并且由于第一轮中交换操作导致 S1[1]=S0[j1] = S0[x]，因此 S1[1] = K[0]+ K[1]+ 1成立。因此，我们假设S0[x]= K[0]+ K[1]+ 1和 S1[1] = K[0]+ K[1]+ 1相互独立。于是，路径2中的概率如下所示：

Pr(S1[x]= K[0]+ K[1]+ 1 \| Path 2)= Pr(S1[1] = K[0]+ K[1]+ 1).

总之，我们得到

Pr(S1[x]= K[0]+ K[1]+ 1) = Pr(S1[x]= K[0]+ K[1]+ 1 \| Path 1)· Pr(Path 1) + Pr(S1[x]= K[0]+ K[1]+ 1 \| Path 2)· Pr(Path 2)
= α1γx−1+(1 − β1)εx,

其中 α1= Pr(S0[1]= K[0]+ K[1]+ 1)， β1= Pr(S0[S0[1]]= K[0]+ K[1]+ 1)， γx−1= Pr(K[0]+ K[1]= x −1) 和 εx= Pr(S0[x]= K[0]+ K[1]+ 1) 由引理 2 给出。

定理7. 在对 0 ≤ x ≤ N执行第 r轮 PRGA之后，我们有

Pr(Sr[ir+1]= K[0]+ K[1]+ 1)
≈
⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨ ⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
α1 if r= 0,
α1γ1+(1 − β1)ε2 if r= 1,
ε0(1 − 1 N) N−1 + 1 N(1 − ε0)(1 −(1 − 1 N) N−1 ) if r= N −1,
ζ1(1 − 1 N) N−1 + 1 N(1 − ζ1)(1 −(1 − 1 N) N−1 ) if r= N,
ζr+1(1 − 1 N) r−1 + 1 N r−1 ∑ x=1 ηx(1 − 1 N) r−x−1 otherwise,

其中 εr是 Pr(S0[r]= K[0]+ K[1]+ 1)，由引理 2给出； ζr是 Pr(S1[r]= K[0]+ K[1]+ 1)，由引理 3给出； ηr是 Pr(Sr[ir+1]= K[0]+ K[1]+ 1)，由该定理给出。

证明。 首先，事件(S0[i1]= K[0]+ K[1]+ 1)和事件(S1[i2]=K[0]+ K[1]+ 1)的概率分别遵循引理2和3的结果。

接下来，事件（SN−1[iN]= K[0]+ K[1]+ 1）和（SN[iN+1]= K[0]+K[1]+ 1）可以采用与定理 5的证明相同的方法进行证明。

最后，事件(Sr[ir+1]= K[0]+K[1]+1)在 2 ≤ r ≤ N−2下的概率可以分解为两条路径： S1[ir+1]= K[0]+ K[1]+ 1（路径1）和Sx[ix+1]= K[0]+ K[1]+ 1(1 ≤ x ≤ r −1)（路径 2）。

路径1。 在S1[ir+1]= K[0]+ K[1]+ 1中，当Sy[iy+1]= S1[ir+1]对于 2 ≤ y ≤ r成立时，事件（Sr[ir+1]= K[0]+ K[1]+ 1）发生，其概率约为(1 − 1 N)r−1。因此，路径1中的概率如下所示：

Pr(Sr[ir+1]= K[0]+ K[1]+ 1 \| Path 1) ≈(1 − 1 N)r−1 .

路径2。 在Sx[ix+1]= K[0]+ K[1]+ 1(1 ≤ x ≤ r − 1)中，如果 jx+1= ir+1，则由于交换操作，Sx+1[ir+1]= K[0]+K[1]+1始终成立。在第 x+1轮之后，若 x+ 2 ≤ y ≤ r满足 Sy[iy+1]= Sx+1[ir+1]，则事件(Sr[ir+1]= K[0]+K[1]+1) 发生，其概率约为(1 − 1 N)r−x−1。因此，路径2中的概率如下所示：

Pr(Sr[ir+1]= K[0]+ K[1]+ 1 \| Path 2) ≈ 1 N(1 − 1 .

注意，在路径2中， x的范围根据 r的值而变化。总之，我们得到

Pr(Sr[ir+1]= K[0]+ K[1]+ 1) = Pr(Sr[ir+1]= K[0]+ K[1]+ 1 \| Path 1)· Pr(Path 1) +
r−1 ∑ x=1 Pr(Sr[ir+1]= K[0]+ K[1]+ 1 \| Path 2)· Pr(Path 2)
≈ ζr+1(1 − 1 N) r−1 + 1 N r−1 ∑ x=1 ηx(1 − 1 N) r−x−1 ,

其中 ζr=Pr(S1[r]= K[0]+ K[1]+1) 和 ηr=Pr(Sr[ir+1]= K[0]+ K[1]+1) 是该定理中的递归概率。

5 实验结果

为了验证定理1–7中所示的显著线性相关性的准确性，使用 240 16字节的随机生成的密钥进行了实验

通用RC4和WPA中的字节，这意味着 240(= N5)次试验。请注意，据报告O(N3) 次试验足以以恒定的成功概率识别偏差。这就是为什么每个相关性相对于概率为 1 N的基础事件具有至少约为 1 实验环境如下：Ubuntu 12.04系统，配备2.6 GHz CPU、3.8 GiB内存、gcc 4.6.3编译器以及C语言。我们还评估了实验值相对于理论值的相对误差百分比 ε：

ε=\|experimental value −theoretical value\| experimental value × 100(%).

表2显示了实验值与理论值以及相对误差的百分比 ε，表明 ε在各种情况下的值足够小，例如 ε ≤ 4.589（%）。图7展示了定理7中实验值与理论值的对比，这些分布总体上吻合良好。因此，我们确信理论值能够很好地反映实验值。

表2. 实验值与理论值的比较

结果	实验值	理论值	(%)
定理1 定理2 对于RC4 定理 3{ for WPA 对于RC4 定理 4{ for WPA 定理5 对于RC4 定理 6{ for WPA	0.001449605 0 0.005332558 0.007823541 0.003922530 0.007851853 0.138038917 0.003909105 0.037186225	0.001445489 0 0.005325263 0.008182569 0.003898206 0.008182569 0.138325988 0.003893102 0.037105932	0.284 0 0.137 4.589 0.620 4.212 0.208 0.409 0.216

6 结论

本文中，我们聚焦于状态信息，研究了通用RC4和WPA中未知状态信息、 RC4密钥的前3字节以及一个密钥流字节之间的各种线性相关性。未知特别是，这些线性相关性对状态恢复攻击有效，因为它们包含了前已知 3字节密钥（与 IV相关）。结果，我们发现了150多个具有正偏差或负偏差的线性相关性。我们还从理论上证明了六个显著线性相关性，即在 S0[i1]、 S255[i256]和 Sr[ir+1] 中关于 0 ≤ r ≤ N的偏差。例如，我们证明了在WPA中(S0[i1]= K[0])的概率为0（见定理2），因此， S0[i1]与 [0, 255]\ K[0]不同。

这些新的线性相关性可能有助于改进针对RC4的WPA环境下的状态恢复攻击。表3中所示的各种线性相关性的理论证明仍然是一个开放性问题。如何将新发现的线性相关性应用于状态恢复攻击也是一个待解决的开放性问题。

一种新获得的线性相关性

在本部分中，表3展示了通过我们在第4.1节所述实验新发现的显著线性相关性。

表3。通用RC4和WPA在公式(1)中的显著线性相关性

Xr	RC4	WPA
S0[i1] (= j1)	−Z1+1 −K[0] − K[1] − K[2] −K[0] − K[1] −3 −K[0] − K[1]+1 −K[0] − K[1]+3 −K[0] −1 −K[0]+2 −K[0]+ K[1] −3 −K[0]+ K[1] −1 K[1]+1 K[0] − K[1]+1 K[0] − K[1]+3 K[0]+ K[1]+ K[2]+3 Z1 − K[0]− K[1]− K[2] −2	0.007584 0 0.005361 0 0.005336 0 0.005350 0 0.005331 0 0.003823 0 0.003902 0 0.005334 0 0.005331 0 0.006765 0 0.005324 0 0.005333 0 0.001492 0 0.005326 0.003905 0
S1[i2]	−Z2 − K[0]+ K[1] −Z2 − K[0]+ K[1]+2 −Z2 − K[1]+ K[2]−3 −Z2 −Z2+2 −Z2+ K[1]+ K[2]+3 −Z2+ K[0] − K[1] −Z2+ K[0] − K[1]+2 −K[0] − K[1] − K[2]+1 −K[0] − K[1] − K[2]+3 −K[0] − K[1]+3 −K[0] − K[1]+ K[2]−3 −K[0] − K[1]+ K[2]−1 −K[0] − K[1]+ K[2]+1 −K[0] − K[1]+ K[2]+3 −K[0]+ K[2] −2 −K[0]+ K[2]+1 −K[0]+ K[1] − K[2]−3 −K[0]+ K[1] − K[2]−1 −K[0]+ K[1] − K[2]+1 −K[0]+ K[1] − K[2]+3 −K[0]+ K[1]+ K[2]−3 −K[0]+ K[1]+ K[2]−1 −K[0]+ K[1]+ K[2]+1 −K[0]+ K[1]+ K[2]+3 −K[1] − K[2] −3 −K[2] −1 −K[2]+1 −K[2]+3 K[2] −3 K[2] −1 K[2]+1 K[2]+3 K[1]+ K[2]+3 K[0] − K[1]− K[2]−1 K[0] − K[1]− K[2]+1 K[0] − K[1]− K[2]+3 K[0] − K[1]+ K[2]−3 K[0] − K[1]+ K[2]−1 K[0] − K[1]+ K[2]+1 K[0] − K[1]+ K[2]+3 K[0] K[0]+ K[1]− K[2]−3 K[0]+ K[1]− K[2]+1 K[0]+ K[1]− K[2]+3 Z 2 − K[1]− K[2]−3 Z 2 + K[1]+ K[2]+3	0.003906 0 0.005314 0 0.007768 0 0.007751 0 0.005317 0 0.003907 0 0.003906 0 0.005348 0 0.005281 0 0.005329 0 0.005307 0 0.005305 0 0.005317 0 0.005305 0 0.003904 0 0.003906 0 0.005293 0 0.005296 0 0.005301 0 0.005300 0 0.005308 0 0.005305 0 0.005306 0 0.005310 0 0.006748 0 0.006127 0 0.003915 0 0.003904 0 0.003910 0 0.003910 0 0.003909 0 0.006219 0 0.008157 0 0.005309 0 0.005302 0 0.005308 0 0.005295 0 0.005290 0 0.005309 0 0.005310 0 0.001455 0 0.005312 0 0.005291 0 0.005304 0 0.005323 0 0.005322 0
S 2 [i 3 ]	−Z 3 − K[0]+ K[1]+3 −Z 3 +3 −Z 3 + K [ 0 ] − K[ 1 ] +3 −K [ 0 ] − K [ 1 ] +2 −K [ 0 ] + K [ 1 ] +3 K [ 0 ]	0 . 003906 0 0 . 007825 0 0 . 003907 0 0 . 005335 0 0 . 003901 0 0 . 001463 0
S 3 [ i 4 ]	−K [ 0 ] − K [ 1 ] − K [ 2 ] −K [ 0 ] − K [ 1 ] +3	0 . 005324 0 0 . 006721 0
S 28 [ i 29 ]	−Z 29 − K [ 0 ] + K [ 1 ] −3	0 . 003906 0
S 29 [ i 30 ]	−Z 30 − K [ 0 ] + K [ 1 ] −2	0 . 003906 0
S 30 [ i 31 ]	−Z 31 − K [ 0 ] + K [ 1 ] −1	0 . 003907 0
S 31 [ i 32 ]	−Z 32 − K [ 0 ] + K [ 1 ]	0 . 003906 0
S 32 [ i 33 ]	−Z 33 − K [ 0 ] + K [ 1 ] +1	0 . 003907 0
S 33 [ i 34 ]	−Z 34 − K [ 0 ] + K [ 1 ] +2	0 . 003906 0
S 34 [ i 35 ]	−Z 35 − K [ 0 ] + K [ 1 ] +3	0 . 003907 0
S 92 [ i 93 ]	−Z 93 + K [ 0 ] − K [ 1 ] −3	0 . 003904 0
S 93 [ i 94 ]	−Z 94 + K [ 0 ] − K [ 1 ] −2	0 . 003906 0
S 94 [ i 95 ]	−Z 95 + K [ 0 ] − K [ 1 ] −1	0 . 003907 0
S95[i96]	−Z96+ K[0] − K[1]	0.003906 0 0.003906 0
S96[i97]	−Z97+ K[0] − K[1]+1	0.003906 0
S97[i98]	−Z98+ K[0] − K[1]+2	0.003906 0
S98[i99]	−Z99+ K[0] − K[1]+3	0.003908 0
S124[i125]	−Z125 − K[0]+ K[1] −3 −Z125+ K[0]+ K[1] −3	0.003906 0 0.003907 0
S125[i126]	−Z126 − K[0]+ K[1] −2 −Z126+ K[0] − K[1] −2	0.003907 0 0.003906 0
S126[i127]	−Z127 − K[0]+ K[1] −1 −Z127+ K[0] − K[1] −1	0.003906 0 0.003908 0
S127[i128]	−Z128 − K[0]+ K[1] −Z128+ K[0] − K[1]	0.003907 0 0.003906 0
S128[i129]	−Z129 − K[0]+ K[1]+1 −Z129+ K[0] − K[1]+1	0.003907 0 0.003906 0
S129[i130]	−Z130 − K[0]+ K[1]+2 −Z130+ K[0] − K[1]+2	0.003906 0 0.003903 0
S130[i131]	−Z131 − K[0]+ K[1]+3 −Z131+ K[0] − K[1]+3	0.003906 0 0.003904 0
S156[i157]	−Z157 − K[0]+ K[1] −3	0.003906 0
S157[i158]	−Z158 − K[0]+ K[1] −2	0.003906 0
S158[i159]	−Z159 − K[0]+ K[1] −1	0.003906 0
S159[i160]	−Z160 − K[0]+ K[1]	0.003906 0
S160[i161]	−Z161 − K[0]+ K[1]+1	0.003907 0
S161[i162]	−Z162 − K[0]+ K[1]+2	0.003907 0
S162[i163]	−Z163 − K[0]+ K[1]+3	0.003907 0
S220[i221]	−Z221+ K[0] − K[1] −3	0.003907 0
S221[i222]	−Z222+ K[0] − K[1] −2	0.003906 0
S222[i223]	−Z223+ K[0] − K[1] −1	0.003907 0
S223[i224]	−Z224+ K[0] − K[1]	0.003908 0
S224[i225]	−Z225+ K[0] − K[1]+1	0.003907 0
S225[i226]	−Z226+ K[0] − K[1]+2	0.003907 0
S226[i227]	−Z227+ K[0] − K[