线性回归算法梳理（初版）

1. 机器学习的一些概念(有监督、无监督、泛化能力、过拟合欠拟合(方差和偏差以及各自解决办法)、交叉验证)

机器学习方法是计算机利用已有的数据(经验)，得出了某种模型(迟到的规律)，并利用此模型预测未来(是否迟到)的一种方法。从广义上来说，机器学习是一种能够赋予机器学习的能力以此让它完成直接编程无法完成的功能的方法。但从实践的意义上来说，机器学习是一种通过利用数据，训练出模型，然后使用模型预测的一种方法。

目前根据是否使用的数据是否标注分为有监督学习、无监督学习和半监督学习等

泛化能力：

泛化能力，主要是指机器学习算法对新鲜样本的适应能力。有一些算法泛化能力差主要是指可能只适合非常特殊的场景，其他一些不同于此场景时该机器学习biab表现很差。通常过拟合的机器学习算法泛化能力差，欠拟合的算法则反之。

交叉验证：

通常交叉验证在前期选择模型时使用！

 

2.线性回归的原理

 

线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。

线性回归的模型函数如下：

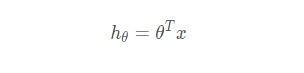
它的损失函数如下：

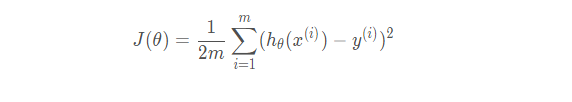
3. 线性回归损失函数、代价函数、目标函数的概念

损失函数（Loss Function ）是定义在单个样本上的，计算的是一个样本的误差。

代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是所有样本损失函数之和的平均。

目标函数（Object Function）定义为：最终需要优化的函数。等于经验风险+结构风险（也就是Cost Function + 正则化项）。

4. 一元线性回归的参数求解公式推导

对于样本集 D = { (x1,y1), (x2,y2), …, (xm,ym) } 线性回归模型就是要找到一个模型f(x)=wx+bf(x)=wx+b 使得 ∀i∈[1,m]∀i∈[1,m] 都有 f(xi) 尽可能地接近于 yi 所以我们使每一个样本的预测值与真实值的差的平方和最小，即：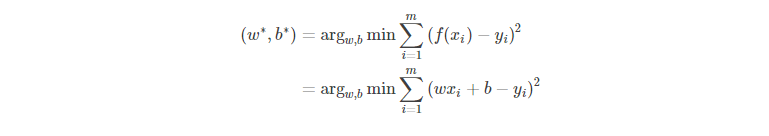 

这可以看做是对多元函数 h(w,b)=∑mi=1(wxi+b−yi)2h(w,b)=∑i=1m(wxi+b−yi)2 求最小值，则按照微积分的知识，函数 h对 w和 b分别求偏导，并令二者的偏导数为零，则此时对应的 w∗w∗ 和 b∗b∗ 便是使得 hh 取最小的值。故，求偏导后得到： 

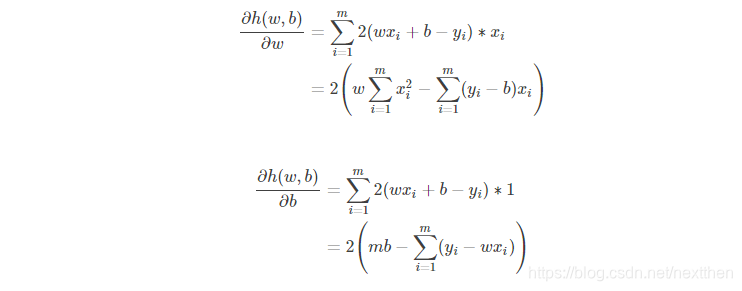
分别令二者等于0便可以得到 w 和 b 的最优解： 

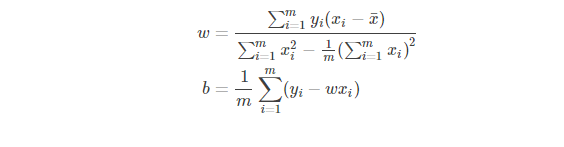
这其中，式(5)是很容易从式(3)得到的，此处不赘述，但是式(4)的得来并没有这么直观，我们来详细推导一下。

令式(2)等于 0 则有：

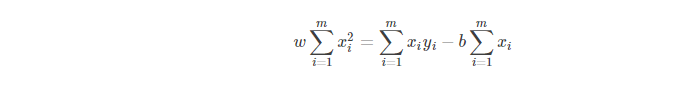
将式(5)代入式(6)得： 

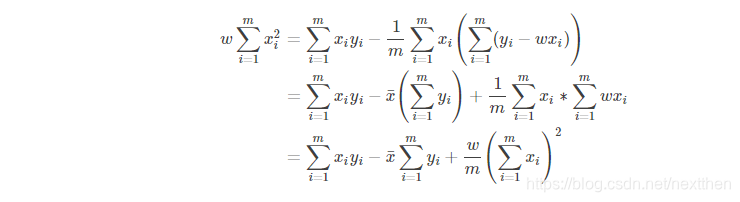
式(7)最右的平方项移项到左边可得： 

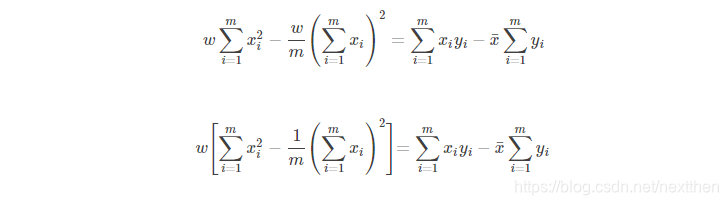
式(8)变形后即可得式(4)，至此，w 和 b 的表达式都只与观测样本有关，所以可以通过样本观测值来估计 w 和 b 。

原文：https://blog.youkuaiyun.com/wx_blue_pig/article/details/79779500 
 

5. 多元线性回归的参数求解公式推导

此处省略，因时间仓促，后面补上。

详细可参考：

https://blog.youkuaiyun.com/weixin_39445556/article/details/81416133

 

6.线性回归的评估指标有哪些？原理是什么？

主要有残差估计、均方误差、决定系数，祥细后期补上

可参照：

https://blog.youkuaiyun.com/mago2015/article/details/84297612

 

7. sklearn参数详解（sklearn包里面线性回归的每个参数的作用）

时间问题，后期补上。

可参照：

https://blog.youkuaiyun.com/gavin__zhou/article/details/50412470