zzuli-2276-跳一跳

最新推荐文章于 2024-05-19 13:13:57 发布

原创最新推荐文章于 2024-05-19 13:13:57 发布 · 356 阅读

1 ·

CC 4.0 BY-SA版权

zzuli 同时被 2 个专栏收录

2 篇文章

订阅专栏

组合数

2 篇文章

订阅专栏

本文介绍了一道ACM竞赛题目，通过杨辉三角特性将问题转化为求组合数C(n+m-4,n-2)。提供了三种实现方法，包括预处理阶乘逆元、快速幂求解以及Lucas定理。

题目链接：http://acm.zzuli.edu.cn/problem.php?id=2276
题目描述
今天跳跳去公园游玩，第一个游戏就难倒了跳跳，游戏规则是跳跳站在一个面积无限大的矩形土地上，开始时跳跳在左上角（即第一行第一列），每一次跳跳都可以选择一个右下方格子，并瞬间跳过去（如从下图中的红色格子能直接跳到蓝色格子），求跳到第n行第m列的格子有多少种方案，答案对1000000007取模。
这里写图片描述
输入
单组测试数据。
两个整数n,m（2<=n,m<=100000）
输出
一个整数表示方案数。
样例输入
4 5
样例输出
10

这题确实很皮！大佬勿喷！

思路一：
一开始我是进行了，手推，发现了规律，但是并没有往杨辉三角上想。
这里写图片描述
打表可以发现这个方法数是一个杨辉三角。
根据杨辉三角的性质，可以知道杨辉三角里面第n行，第m列的数值为C(n-1,m-1)。

然后就是对应关系了。（可能本人比较菜，推了好半天）

第i行第j个对应杨辉三角第i+j-1行第i个

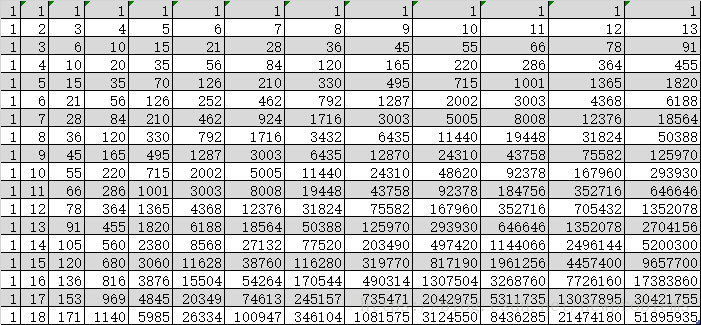
这里写图片描述

本题则是求组合数C（n + m - 4, n - 2）或 C（n + m - 4, m - 2）。

AC ONE
用逆元、费马小定理来求组合数。

//带有预处理
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
const ll maxn = 1e6 + 3;

ll fac[maxn], inv[maxn];

ll quickpow(ll x, ll n)
{
    ll ret = 1;
    ll tmp = x % mod;

    while(n)
    {
        if(n & 1)
        {
            ret = (ret * tmp) % mod;
        }
        tmp = tmp * tmp % mod;
        n >>= 1;
    }
    return ret;
}

void init()
{
    fac[0] = 1;
    for(int i = 1; i < maxn; i++)
    {
        fac[i] = fac[i - 1] * i % mod;
    }
    inv[maxn - 1] = quickpow(fac[maxn - 1], mod -  2);
    for(int i = maxn - 2; i >= 0; i--)
    {
        inv[i] = inv[i + 1] * (i + 1) % mod;
    }
}
ll C(ll a,ll b)
{
    if(b > a)
        return 0;
    if(b == 0)
        return 1;
    return fac[a] % mod * inv[b] % mod * inv[a - b] % mod;
}

int main()
{
    init();
    ll n, m;
    scanf("%lld%lld", &n, &m);
    printf("%lld\n", C(n + m - 4, n - 2));
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=1000005, mod=1e9 + 7;
ll fac[maxn];

void init()
{
    fac[0] = fac[1] = 1;
    for(ll i = 2; i < maxn; i++)
        fac[i] = fac[i - 1] * i % mod;
}

ll quickpow(ll a, ll b)
{
    ll ans = 1;
    while(b)
    {
        if(b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return ans;
}

ll C(ll a, ll b)
{
    return fac[a] * quickpow(fac[b], mod - 2) % mod * quickpow(fac[a - b], mod - 2) % mod;
}
int main()
{
    init();
    ll n, m;
    scanf("%lld%lld", &n, &m);
    printf("%lld\n", C(n + m - 4, n - 2));
    return 0;
}

AC TWO

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;

ll quickpow(ll x, ll n)
{
    ll ret = 1;
    ll tmp = x % mod;

    while(n)
    {
        if(n & 1)
        {
            ret = (ret * tmp) % mod;
        }
        tmp = tmp * tmp % mod;
        n >>= 1;
    }
    return ret;
}

ll C(ll a,ll b)
{
    if(b > a)
        return 0;
    ll ans = 1;
    for(int i = 1; i <= b; i++)
    {
        ll n = (a + i - b) % mod;
        ll m = i % mod;
        ans = ans * (n * quickpow(m, mod - 2) % mod) % mod;
    }
    return ans;
}

ll lucas(ll a, ll b)
{
    if(b == 0) return 1;
    return C(a % mod, b % mod) * lucas(a / mod, b / mod) % mod;
}

int main()
{
    ll n, m;
    scanf("%lld%lld", &n, &m);
    printf("%lld\n", lucas(n + m - 4, n - 2));
    return 0;
}