大学生数学竞赛,不是数学建模,分为数学组和非数学组,我是非数学组。
全国初赛只考高数,全国总决赛考高数和线性代数。当年我是我们学校唯一 一个进入全国总决赛的,非数学组就我一个,数学组全军覆没。
下面贴一下我当年的笔记和习题:
目录
一,知识点
1,达布定理
若f在[a,b]上可导,,则对
、
之间的任意数k,都有
2,达布定理的推论
若f在区间I上满足导数不为0恒成立,则f在I上严格单调
3,施笃兹定理(Stolz)
若数列{bi}递增无上界, 存在或者为正负无穷
则
4,导数公式
5,泰勒展开公式
6,柯西不等式
设f(x), g(x)在区间[a,b]上连续, 则
7,积分中值定理
设f(x)在区间[a,b]上可连续, g(x)在区间[a,b]上可积且不变号,则
二,极限题
1,施笃兹定理
(1)
证明:
递减
(2)
解:
2,其他极限题
(1),证明
时,
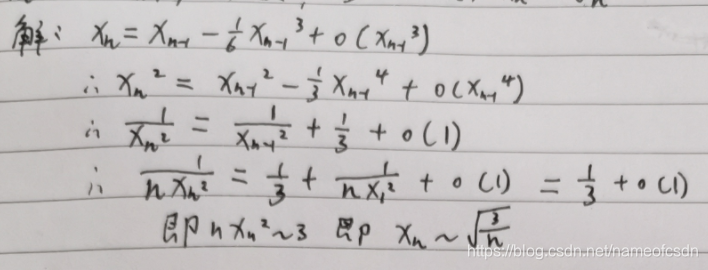
(2)
解:
(3)
证明:
(4)
证明
存在并求它
解:
方法1 ( 我的方法)
存在, 设为c
由于柯西不等式,
方法 2 (书上的方法)
同理,
(2) (证明和上面差不多, 略)
(5),求
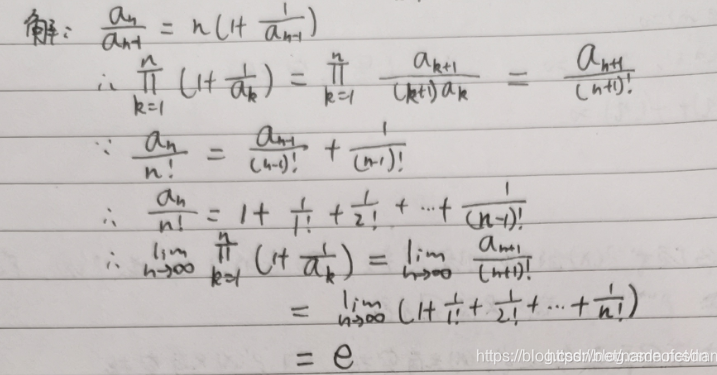
(6)求

(7)求证
(8)求

(9)f(x)在[a,b]上连续且非负,最大值为M,求证:

三,罗尔定理、中值定理、达布定理
1,罗尔定理
(1)f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0, f(1)=0,f(1/2)=1,证明

(2)f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0, f(1)=0,f(1/2)=1
证明:
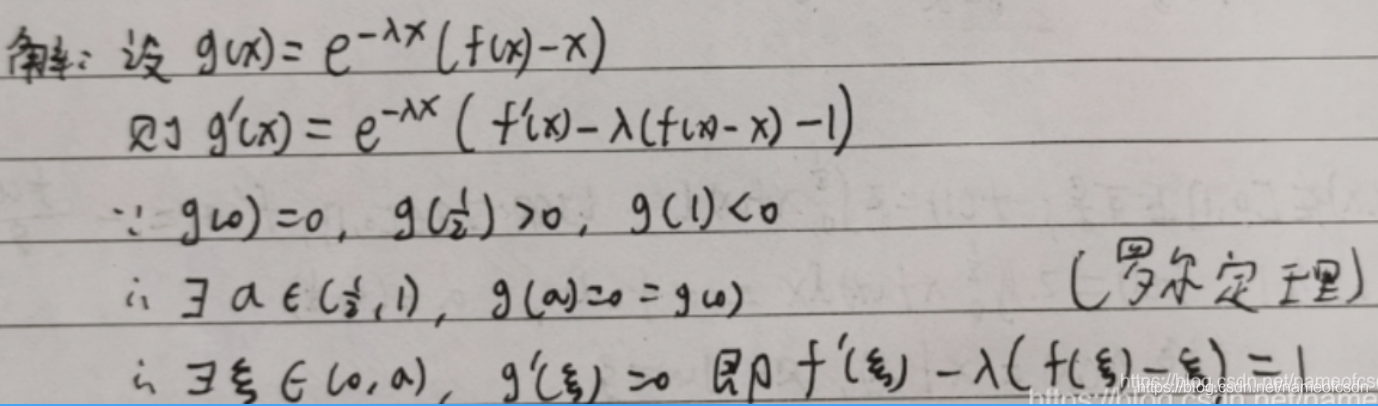
(3)fk可导,f(a)=f(b)=0,证明
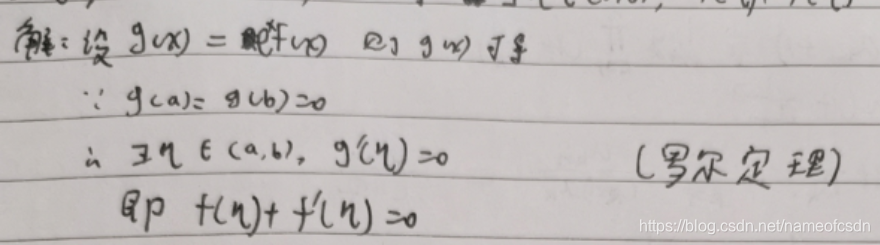
(4)证明:若n次实系数多项式P(x)的n个根都是实数,则它的各阶导数P'(x)、P''(x)、... 都只有实根

(5)f(x)和g(x)在[a,b]上二阶可导,f(a)=f(b)=g(a)=g(b)=0,
证明:
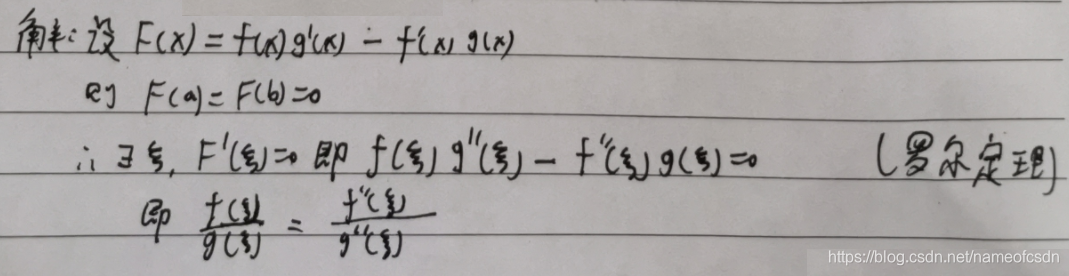
2,微分中植定理
(1)f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0, f(1)=1,证明:
① ②
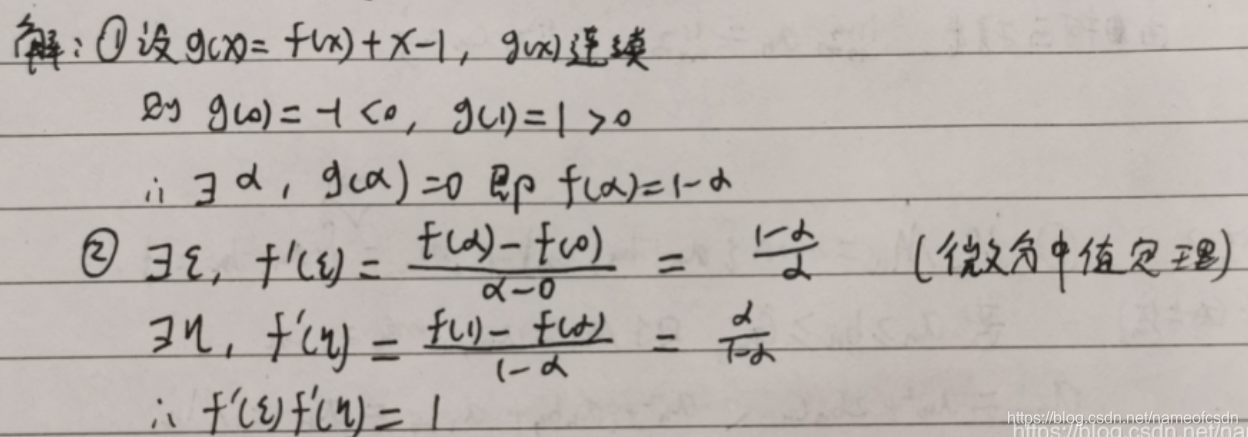
(2)已知f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0, f(1)=1/3,证明:
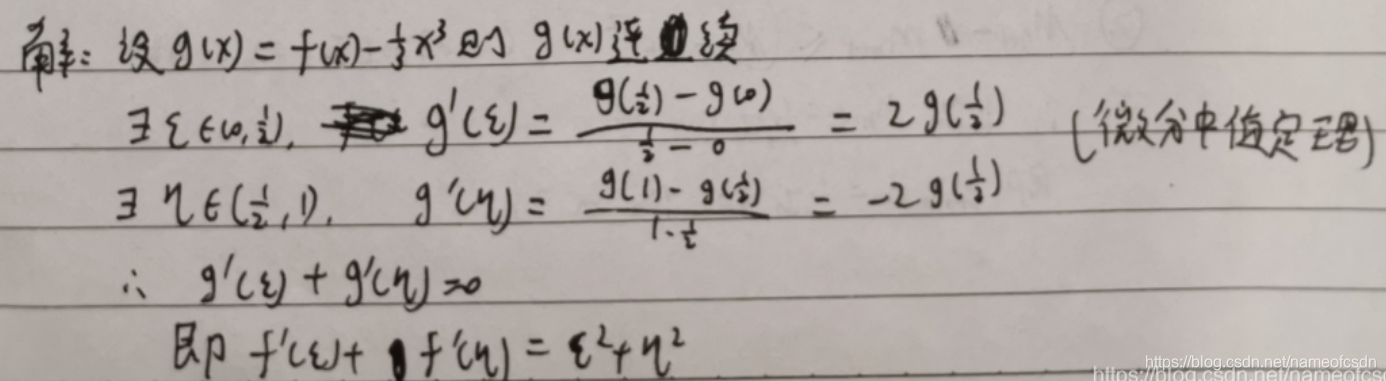
(3)f(x)在[0,1]上可导,且f(0)=0, f(1)=1, ,证明:存在3个不同的数
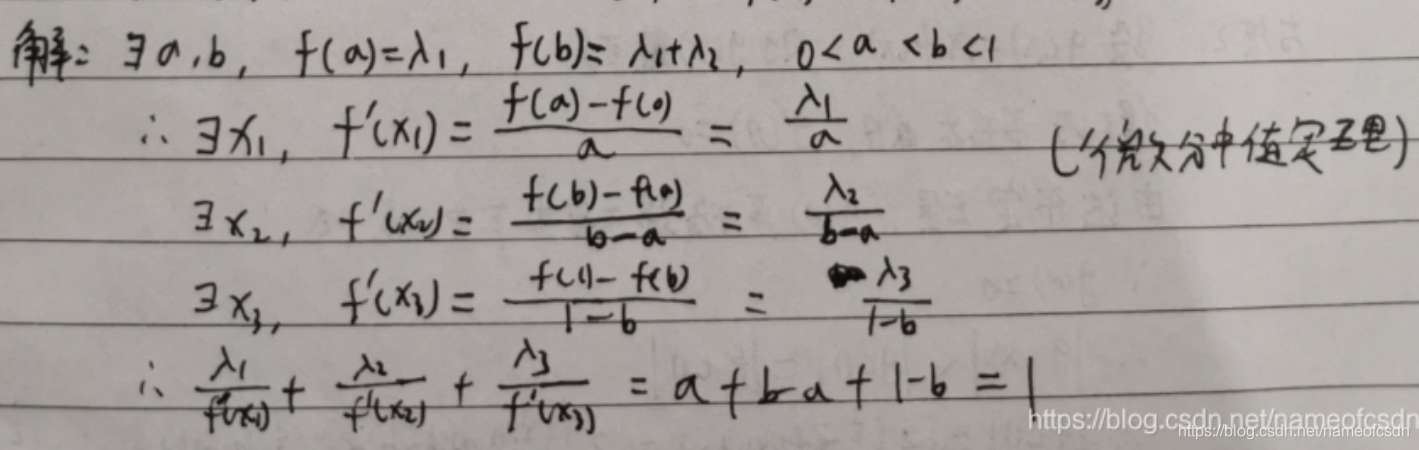
3,柯西中值定理
(1)f(x)在[0,1]上连续,在(0,1)内可导,且f'(x)≠0,证明
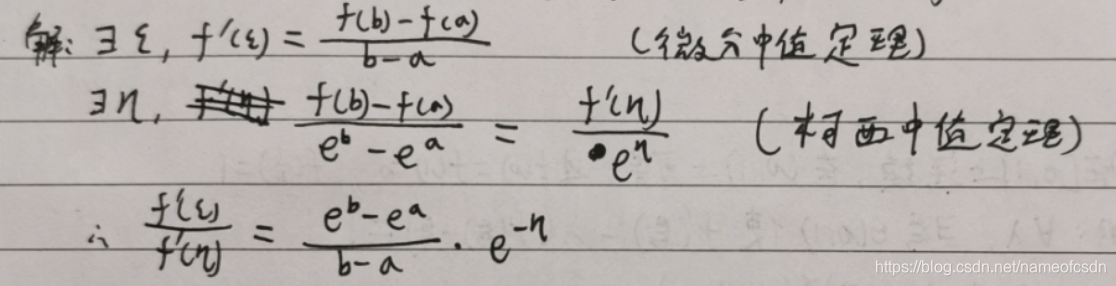
4,积分中值定理
(1)f(x)在[a,b]上有连续的导数,证明
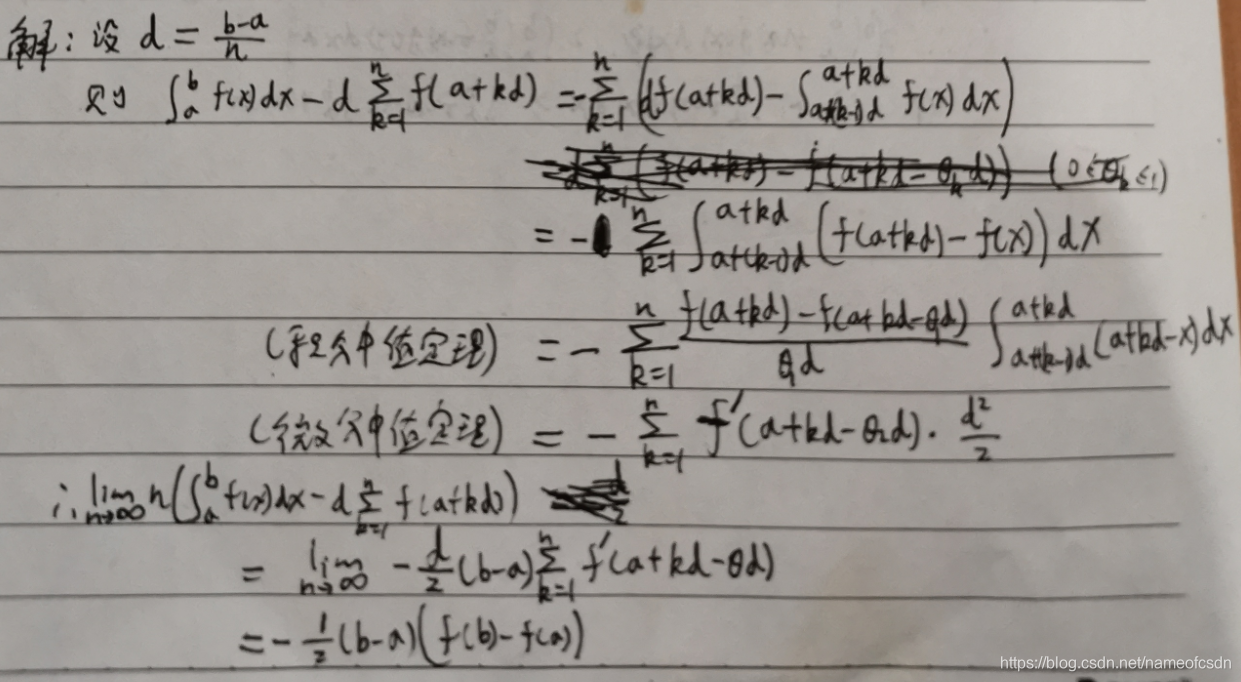
5,达布定理
(1)f(x)在[0,1]上可导,,证明

(2)f(x)二次连续可微,,证明:

(3)设f(x)在上可导,
,证明

四,积分
1,定积分
(1)求
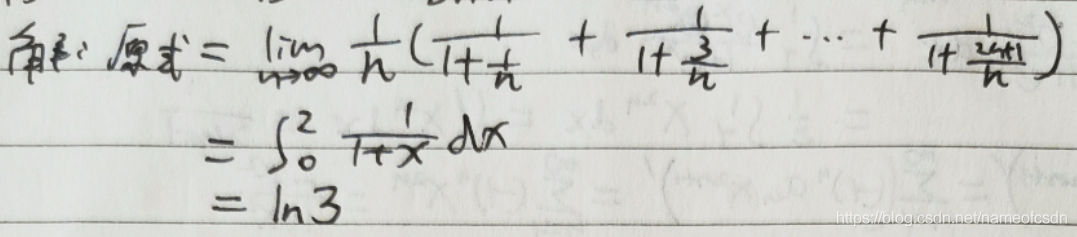
(2)求
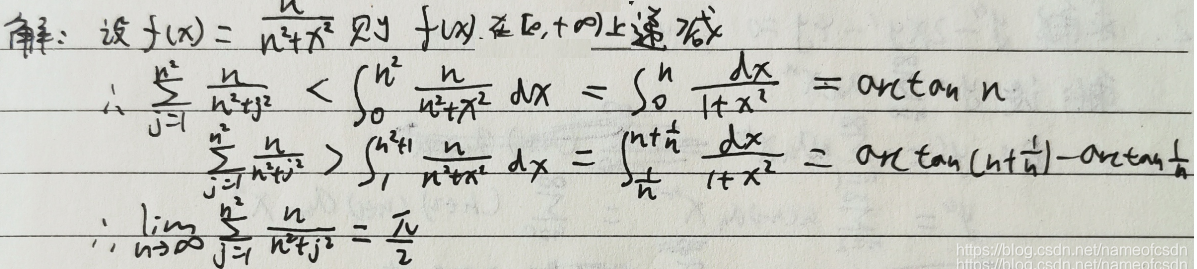
(3)p>0,求
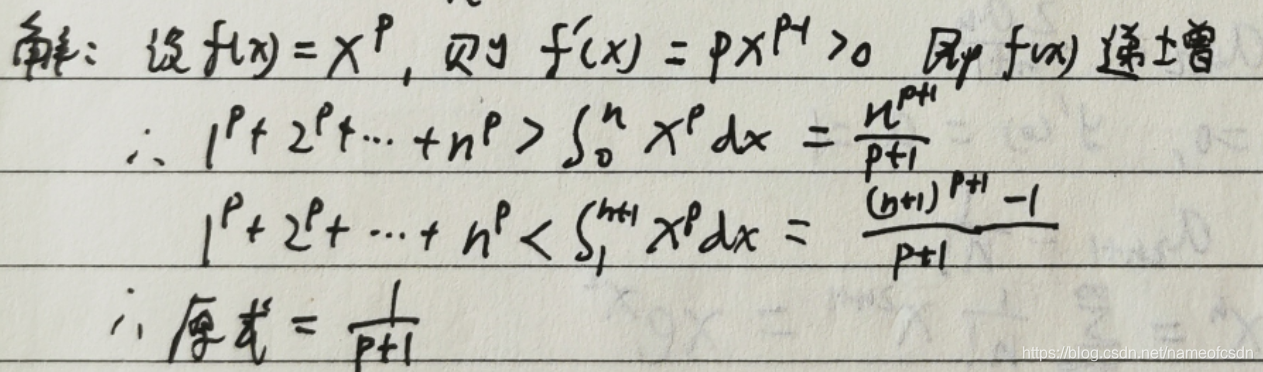
2,二重积分
(1),求

(2),求
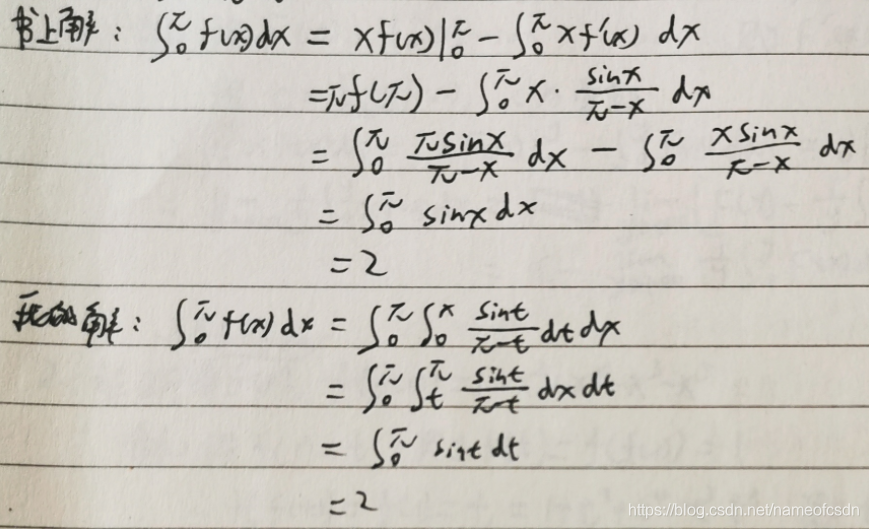
3,积分上限函数
(1)f(x)在[0,1]上可导,0<=f'(x)<=1, f(0)=0, 证明
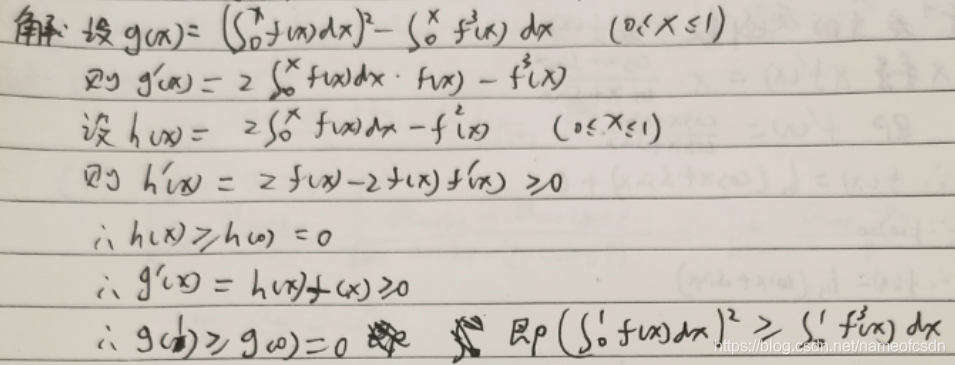
(2)f(x)在[a,b]上连续且严格递增,证明

(3)f(x)在内连续,
,求f(x)
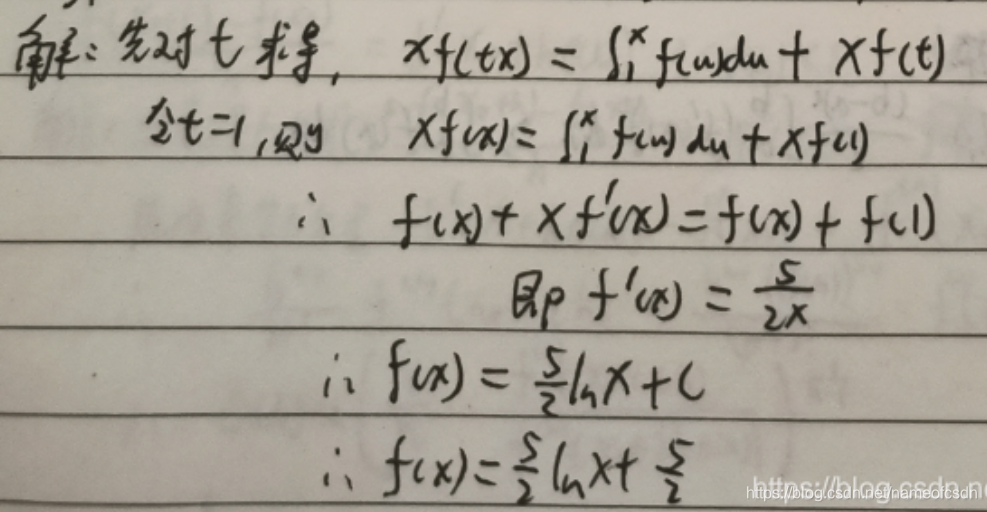
(4)f(x)在 上可导且单调,
,其中
是f的反函数,求f(x)
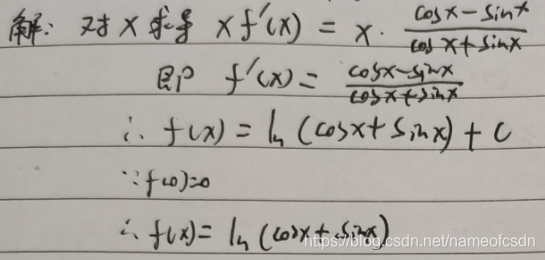
(5)f(x)连续,,求
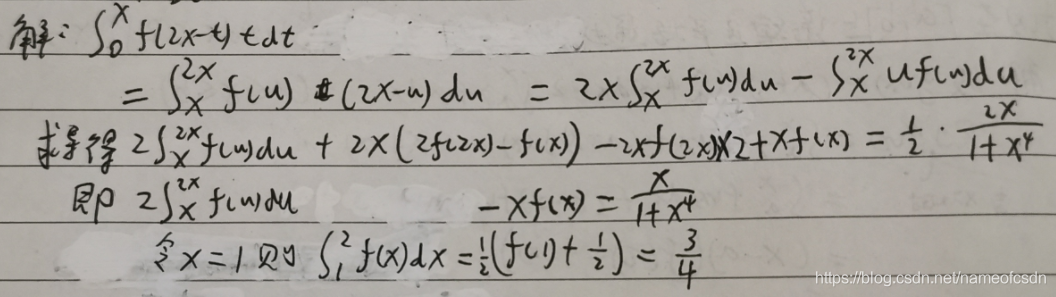
(6)设函数f(x)在[a.b]上有连续导数,f(a)=0,证明
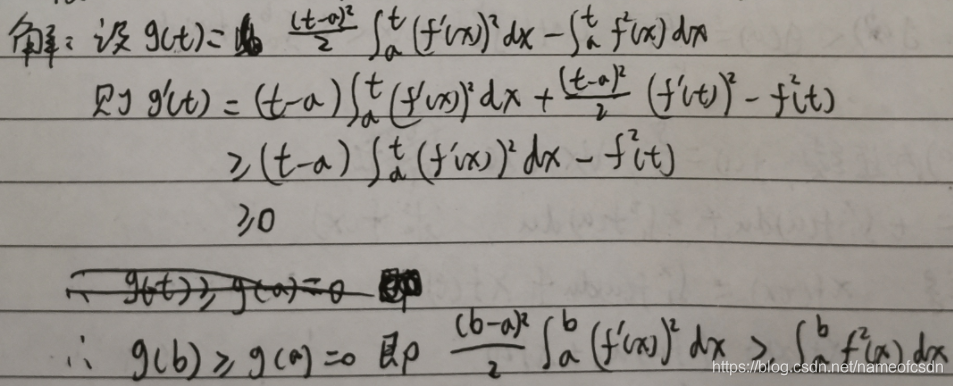
五,微分方程
1,普通微分方程
(1),其中常数
,求f(x)
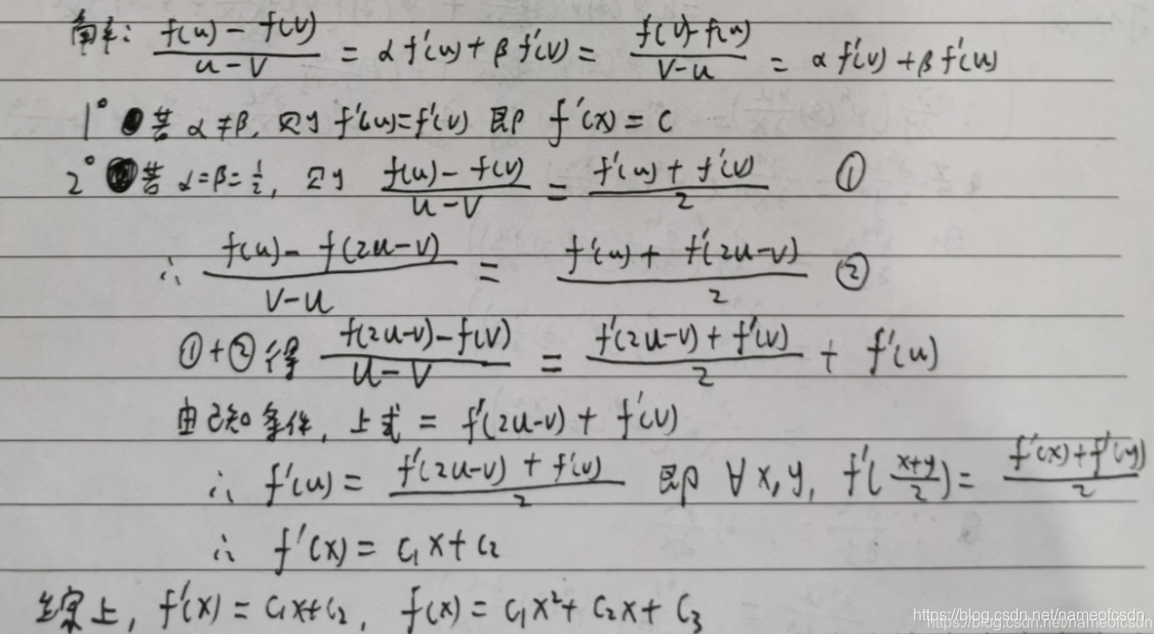
(2)f(x)二次可微,f(x)+f''(x)=-xg(x)f'(x),∀x, g(x)>=0,证明|f(x)|有界

2,特殊微分方程
(1)求解

(2),g(x)为任意给定函数,证明:若f(a)=f(b)=0,则f(x)在[a,b]恒为0

六,导数相关
(1)求 y=arctan x 在 x=0 处的 n 阶导数
解:
由莱布伦茨公式,
so 在 x=0 处,
so 当 n 为偶数时,
当 n 为奇数时,
(2)f(x)在[0,2]上二阶可导,∀x∈[0,2],|f(x)|<=1, |f''(x)|<=1, 证明∀x,|f'(x)|<=2
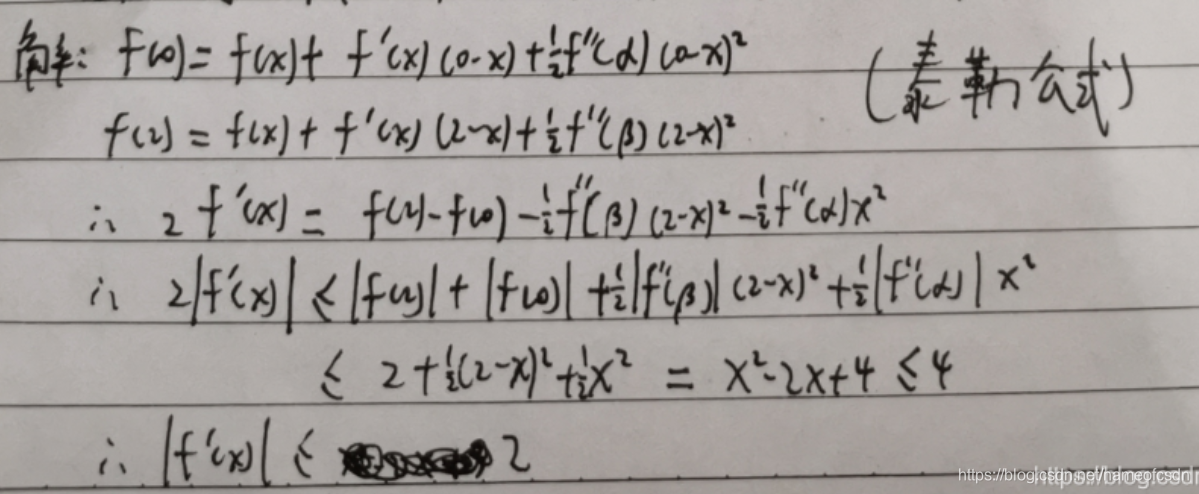
(3)f(x)在点可导,
,证明:
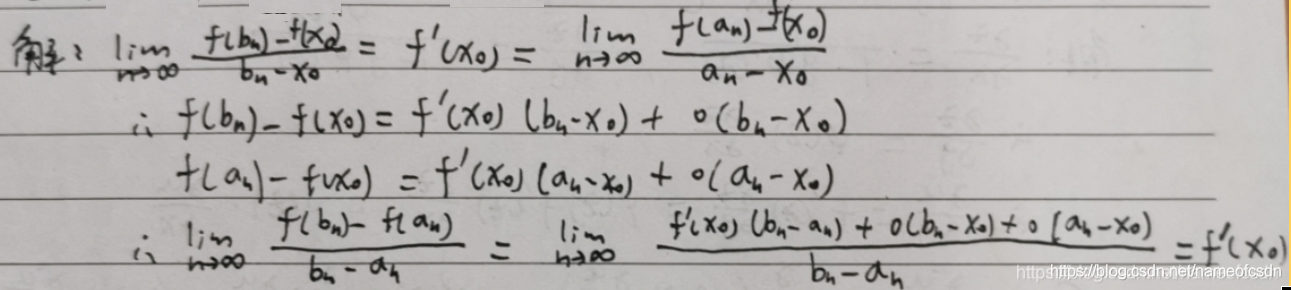
(4)设f(x,y)在上连续,
,其中k是正整数,证明:f为常数

(5)u=f(z),z由方程z=x+yφ(z)确定,φ和f任意次可微,证明:

(6)设f(x,y)有一阶连续偏导数,且f(0,1)=f(1,0)
证明:在圆x^2+y^2=1上存在2个不同的点满足方程
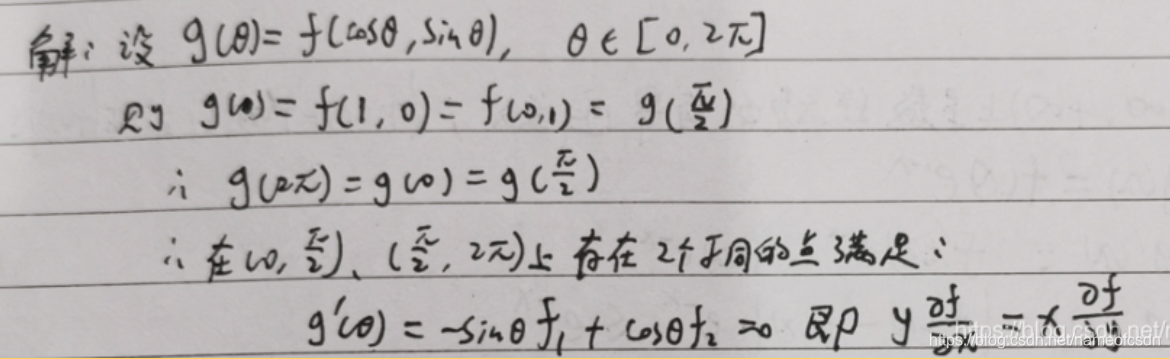
(7)设f(x)在内具有二阶连续导数,
,证明

(8)f(x)是在上导数连续的有界函数,|f(x)-f'(x)|<=1,证明:|f(x)|<=1
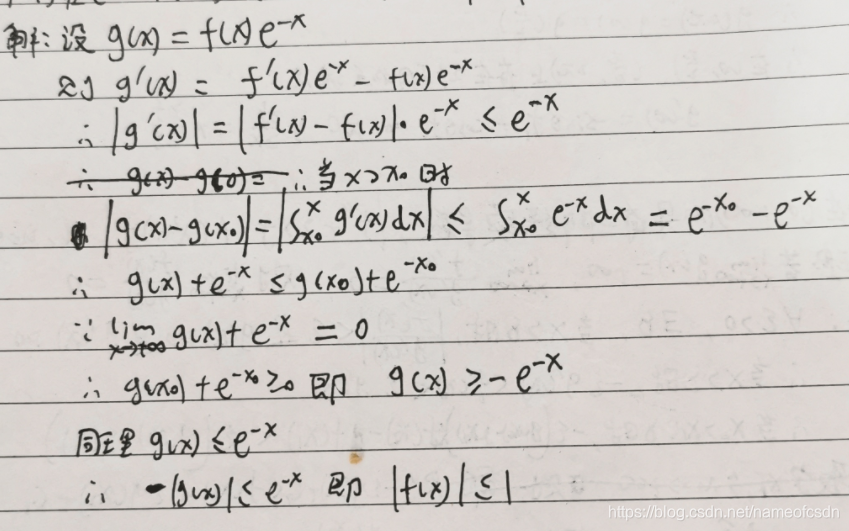
七,易错题
(1)求a,b,使 存在
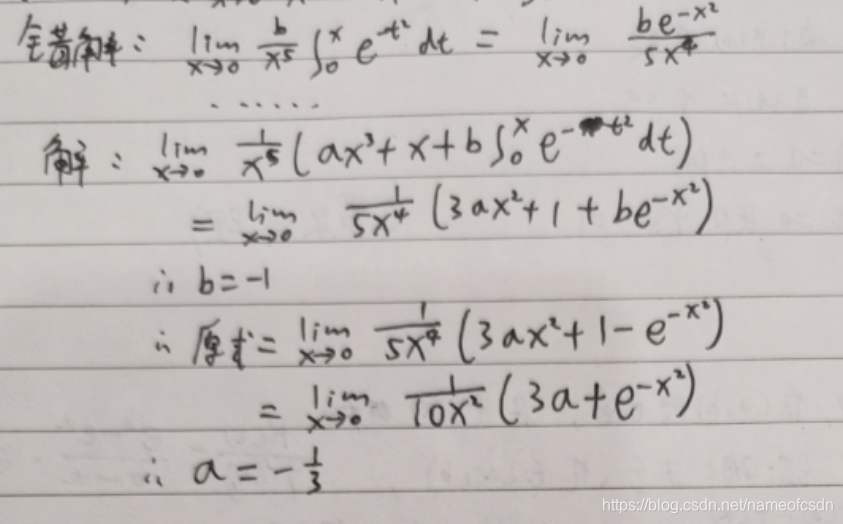
(2)F(0)>0, F'(0)=c, 求
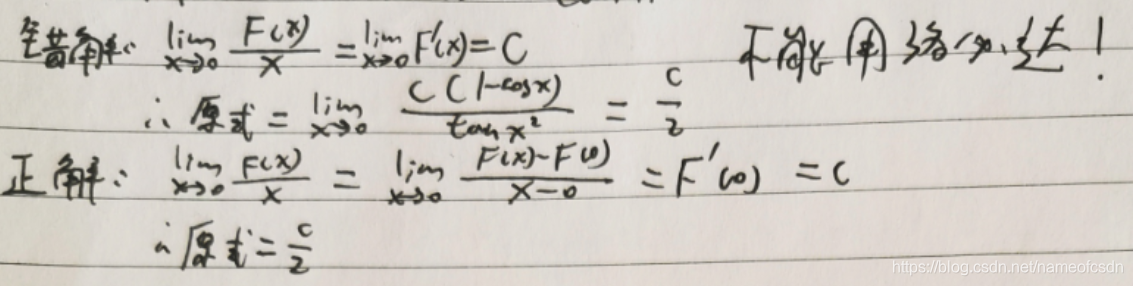
(3)∀ x>0,y>0 都有f(xy)=xf(y)+yf(x), f'(1)=4, 求f(x)
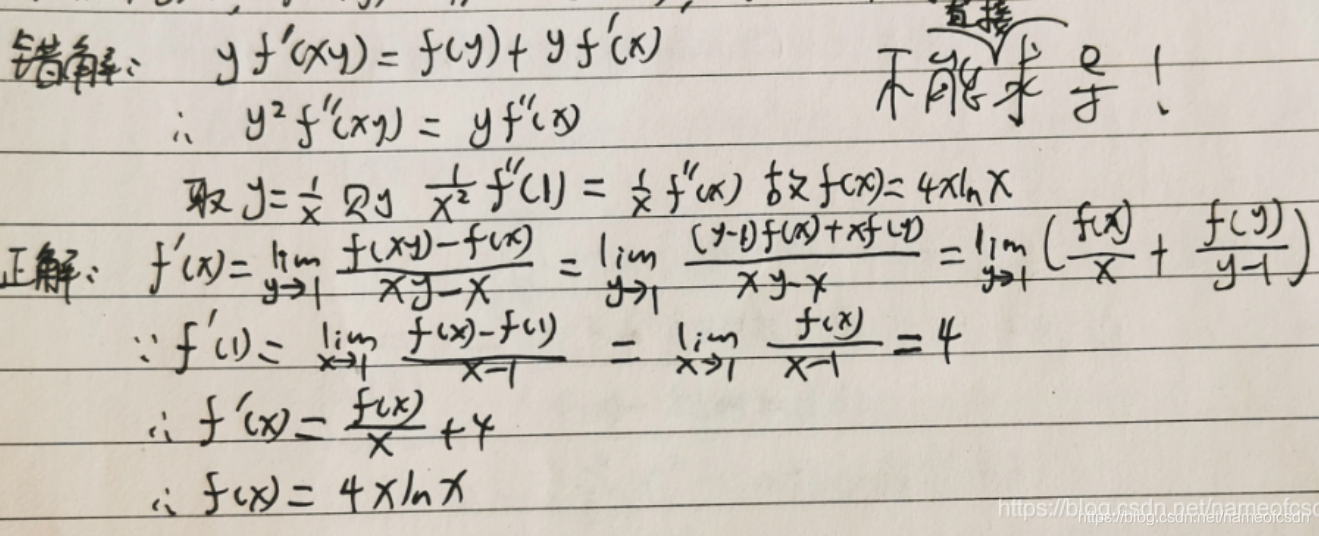
(4)设 , 则f(x)的以2π为周期的Fourier级数在[-π,π]上的和函数为

八,难题
1,设f(x)在[a,b]上具有连续导数,证明:

2,设f(x)在[a,b]上具有二阶导数,证明

3,f(x)周期为π,g(x)周期为1,f(x)、g(x)连续,,证明f(x)=g(x)

4,求
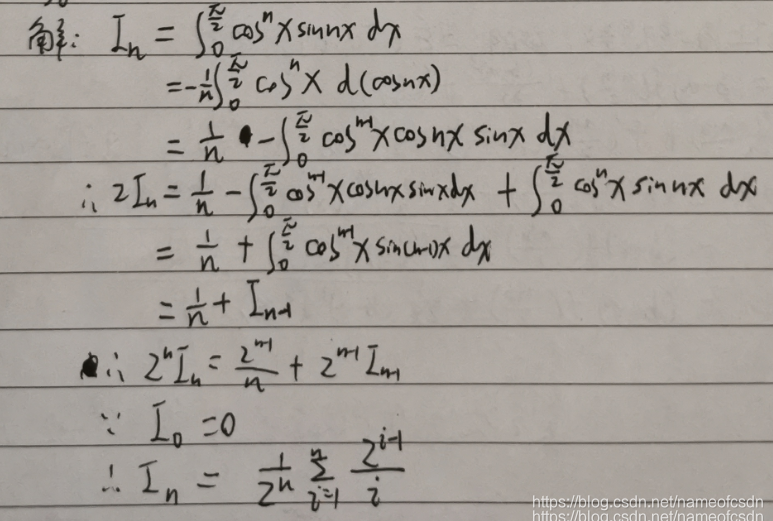
5,设f(x)在[0,1]上可微,f(0)=0,f(1)=1,为n个正数,证明:存在(0,1)内n个不等的数
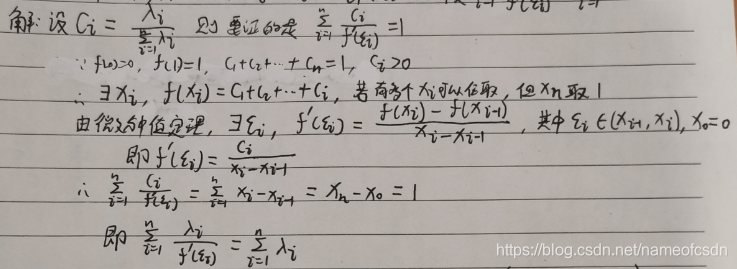
6,设f(x)在[0,1]上连续可微,证明

7,设f(x)在[a,b]上连续,证明
8,设,其中
,当i不为k时,
且f(x)有n个不同的实根,证明
九,解题技巧
1,逐项求导法(生成函数法)
(1),求
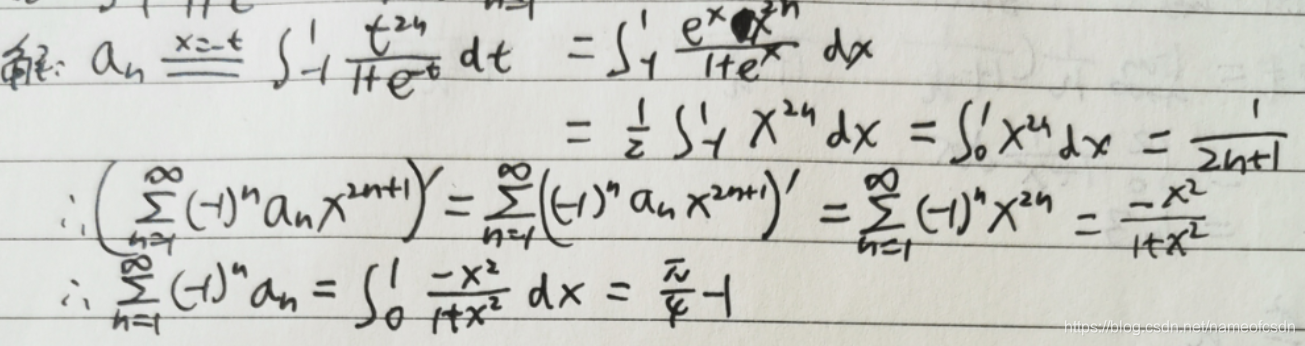
(2)求解y''-2xy'-4y=0, y(0)=0,y'(0)=1
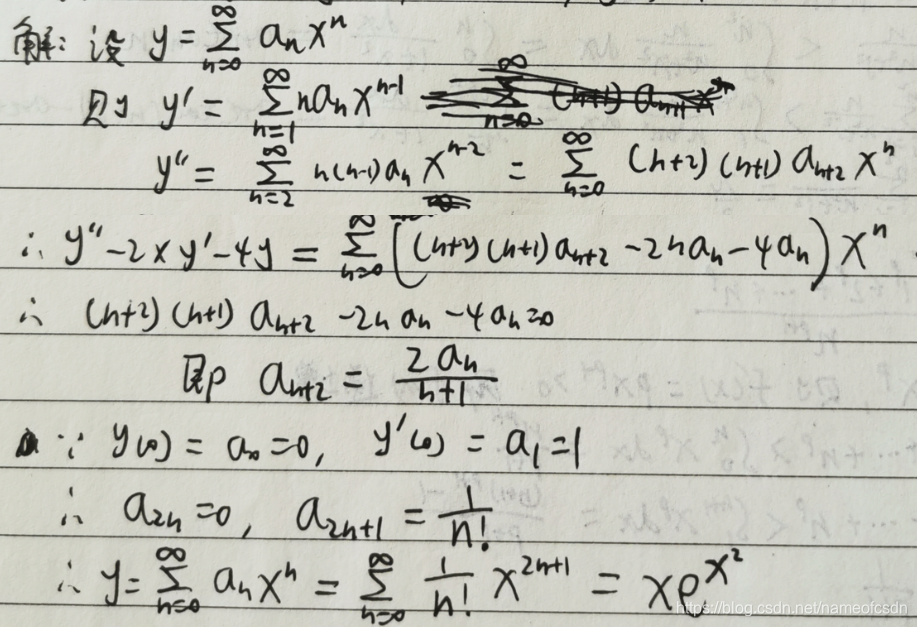
2,交换求和顺序法
(1)求

(2)求

(3)求

(4)黎曼zeta函数,证明
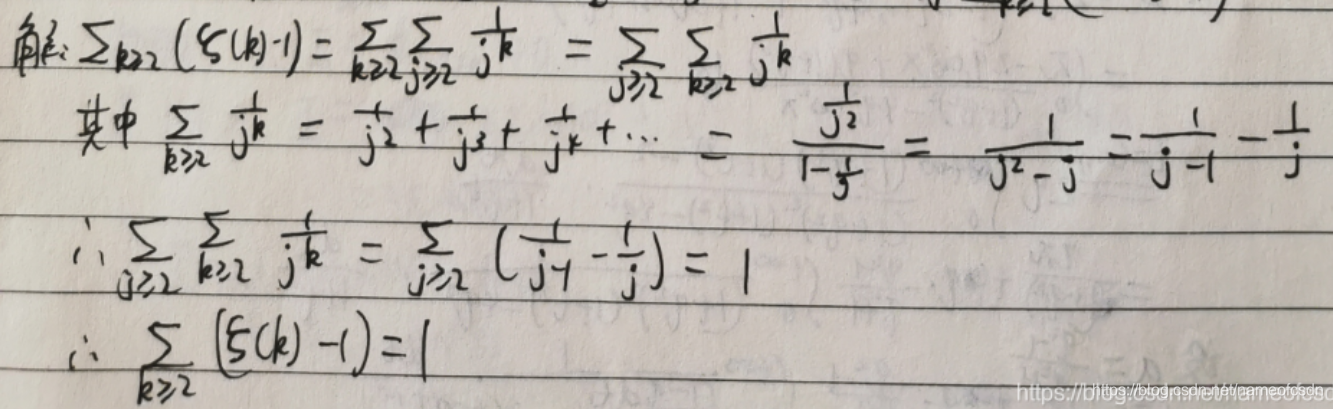
3,特殊的极坐标用法
(1)f(x,y)可微,,证明:f为常数

(2)f(x,y)可微,,证明:f在极坐标中是关于r的函数

4,定义法
(1),证明A>=e

(2)设f(x)在内可微,且
,证明
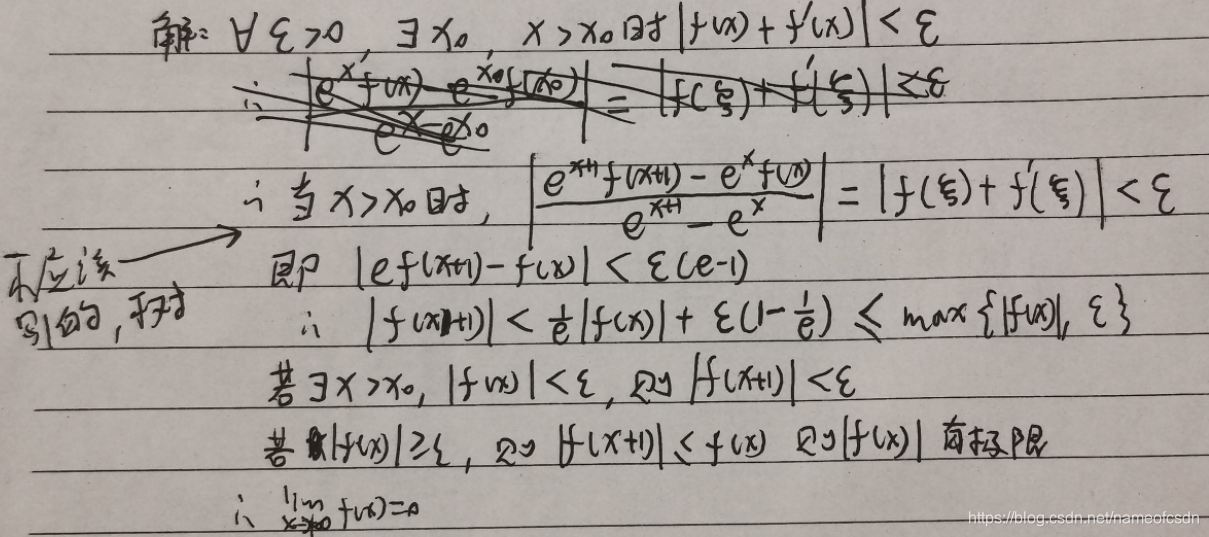
(3)证明,其中f(x)连续

(4)f(x)、g(x)在上连续且周期为1,求证

5,其他特殊方法
(1),求
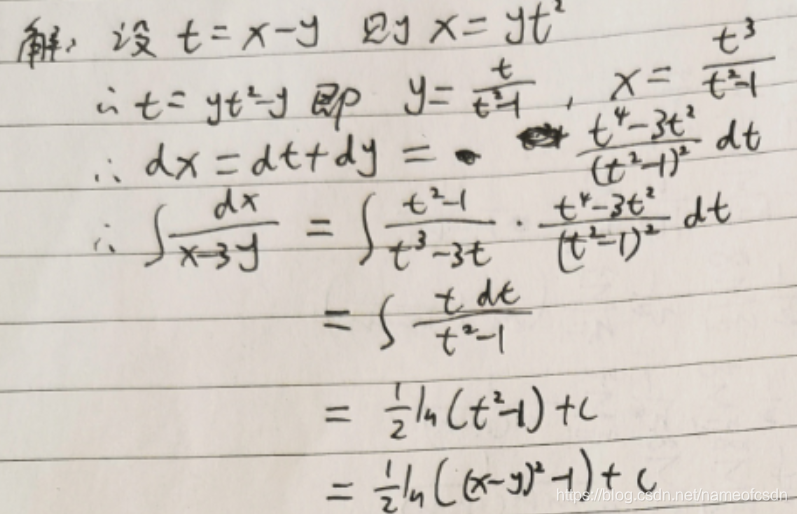
(2)1<f(x)<3,证明
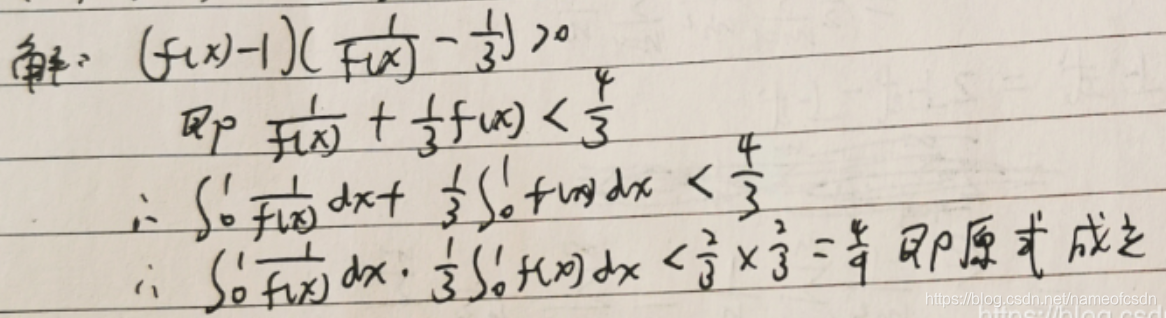
(3)求

(4)f(u)连续,,证明

(5)求
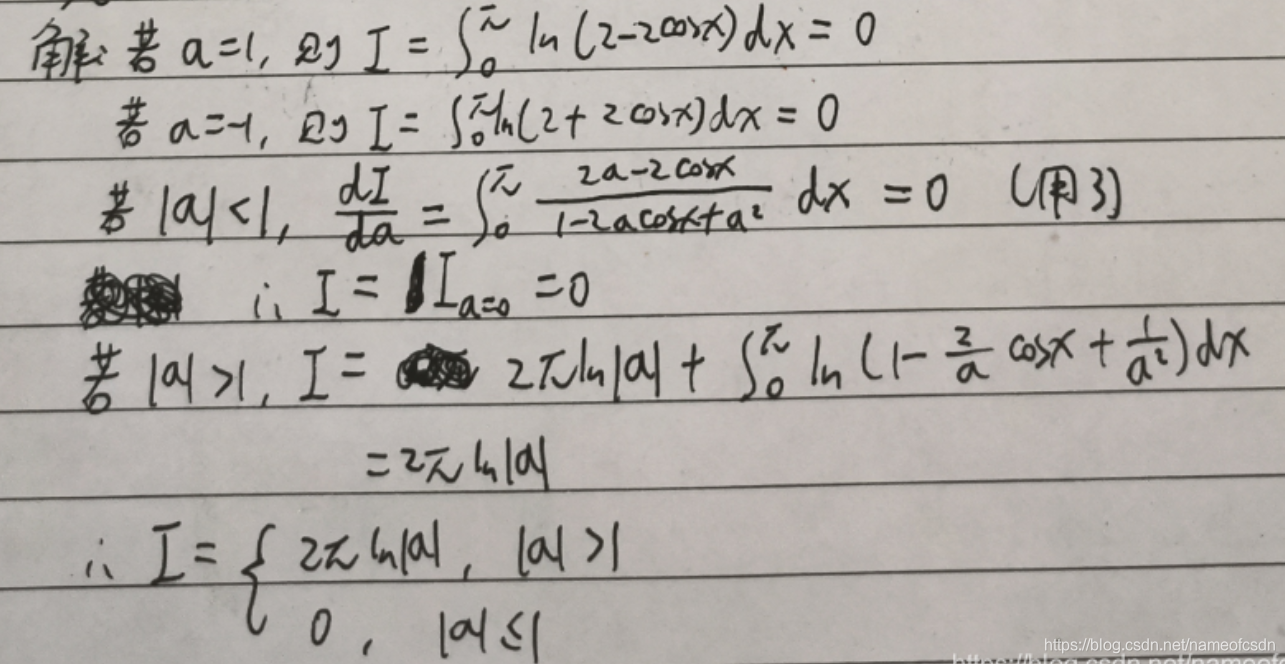
十,反常规题
1,,求

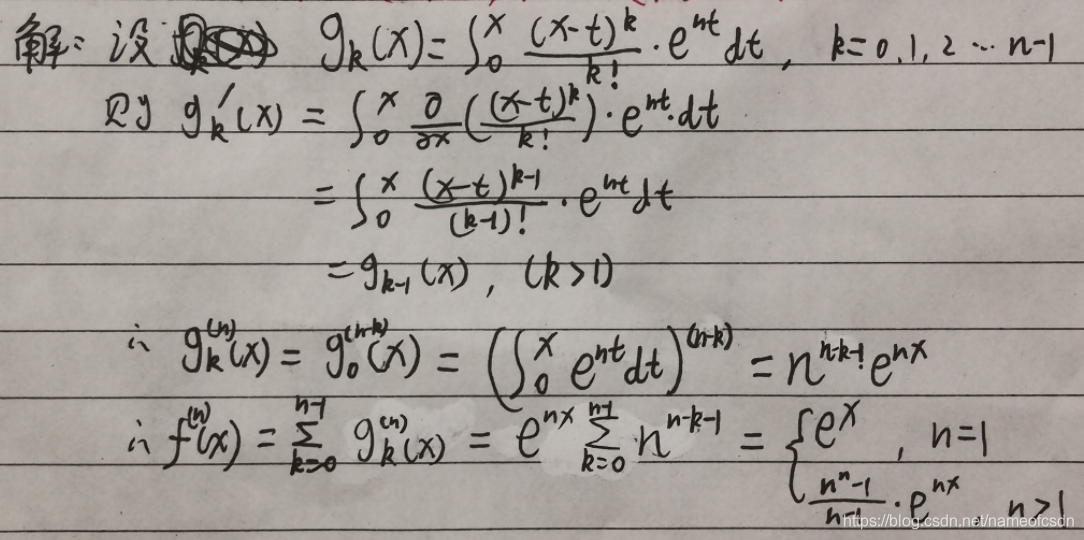
十一,其他题目
1,设f(x)在上连续,
收敛,求
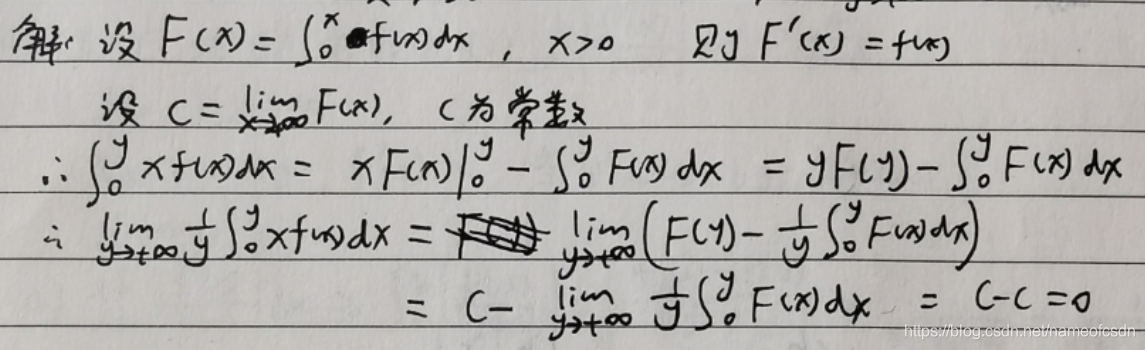
2,证明不存在可导的f(x),
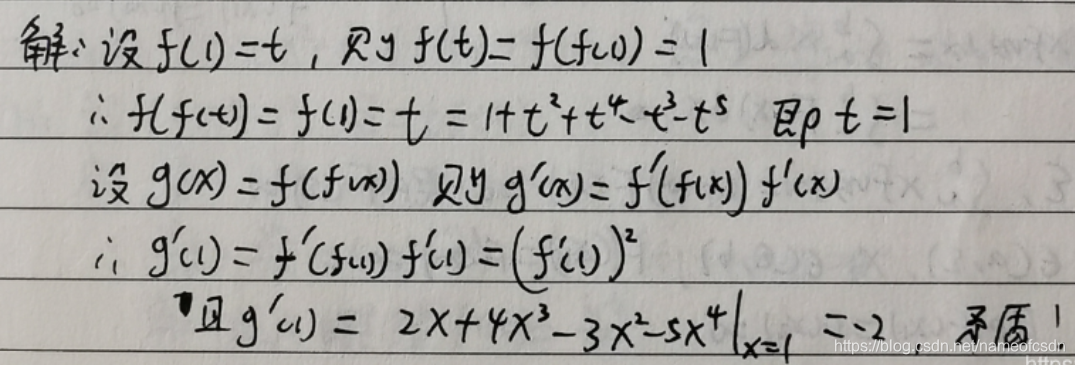
3,f(x)在[a,b]上连续,在(a,b)上可导,,证明:
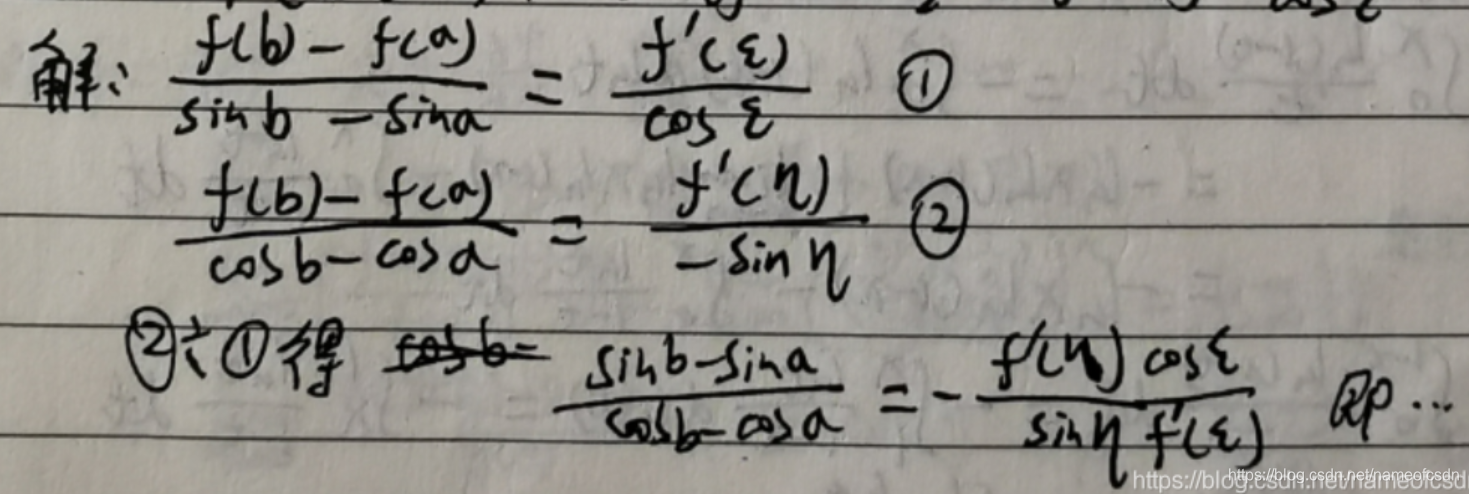
4,f''(x)连续,f''(x)>0, f(0)=f'(0)=0, u=x-f(x)/f'(x),求
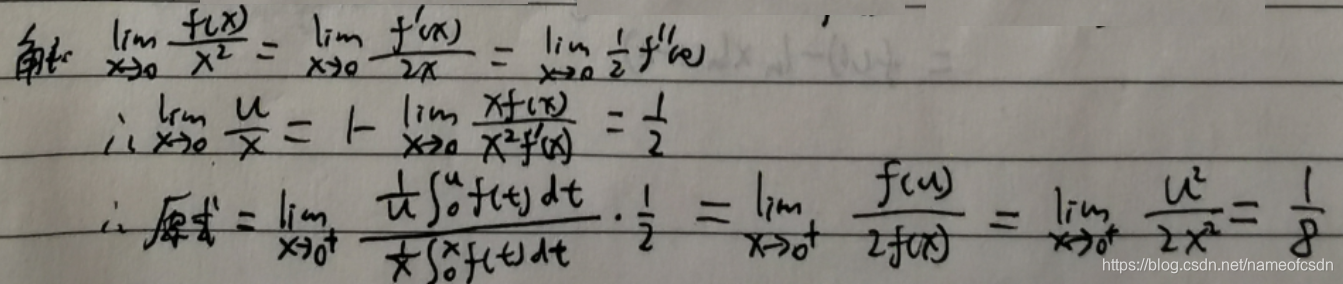
5,求
6,f(x)在[a,b]上连续,,证明
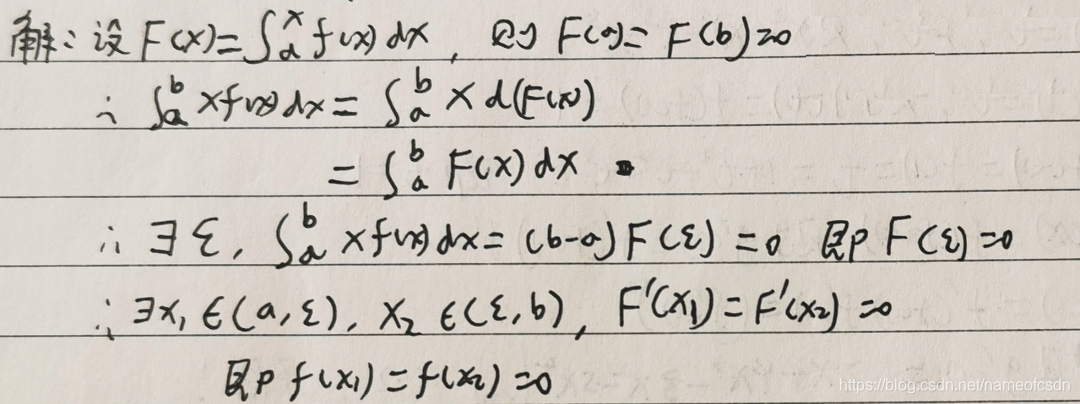
7,,证明:f(x)+f(1-x)=f(1)-lnxln(1-x)
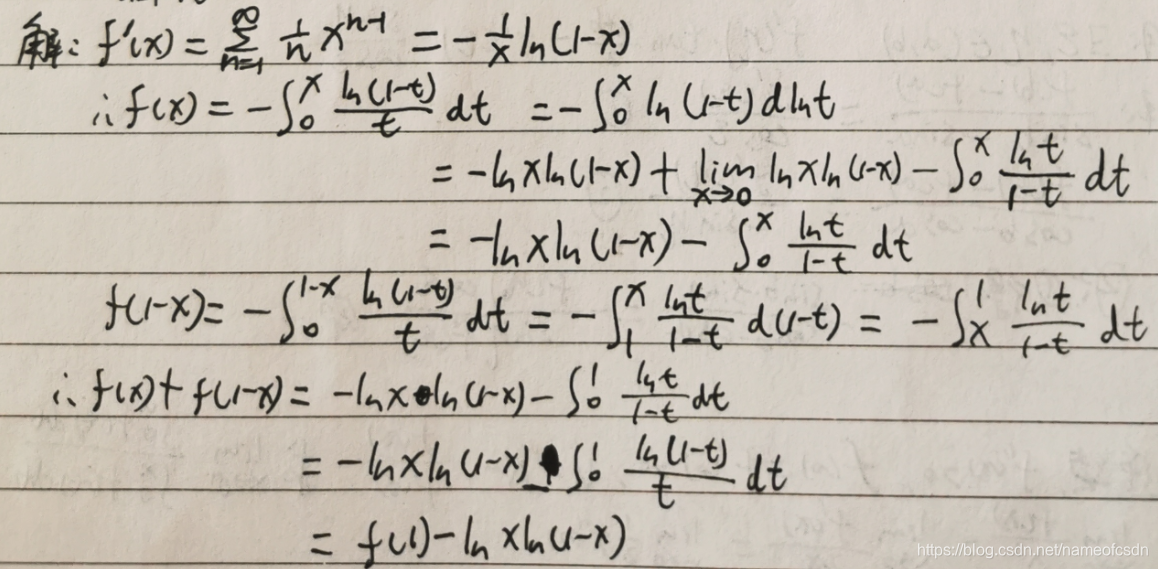
8,设f(x)在[a,b]上具有二阶连续导数,f''(x)<0, f(a)=f(b)=0,
证明:(1)当时,f(x)>0 (2)
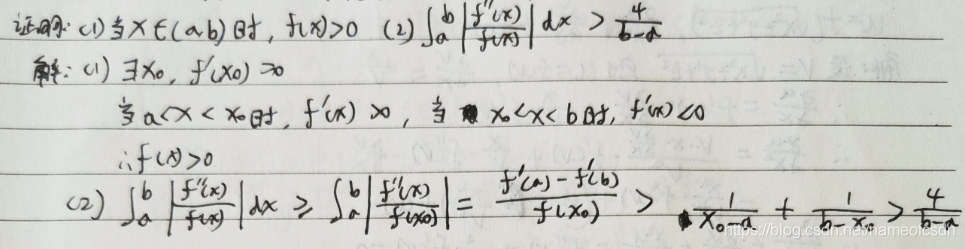
9,f(x)在上有连续的二阶导数,f'(1)=1,f(1)=0,且二元函数
满足
,求f(x)最大值

10,设f可微,,求f
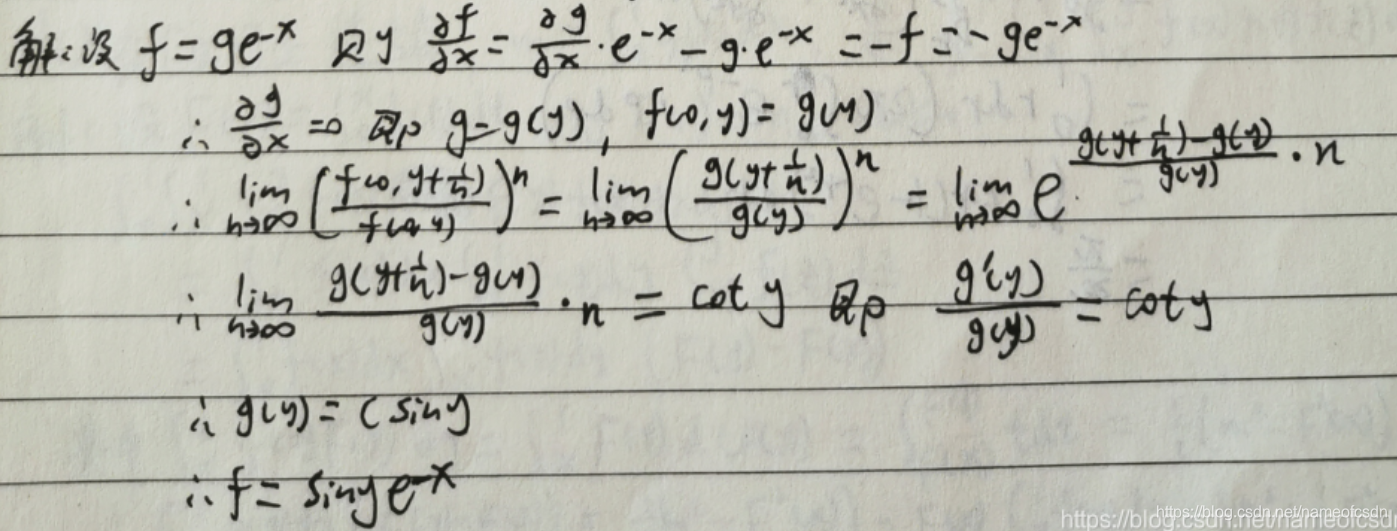
11,设f(t)在上有连续的二阶导数,f(1)=0, f'(1)=1,
,求f(t)
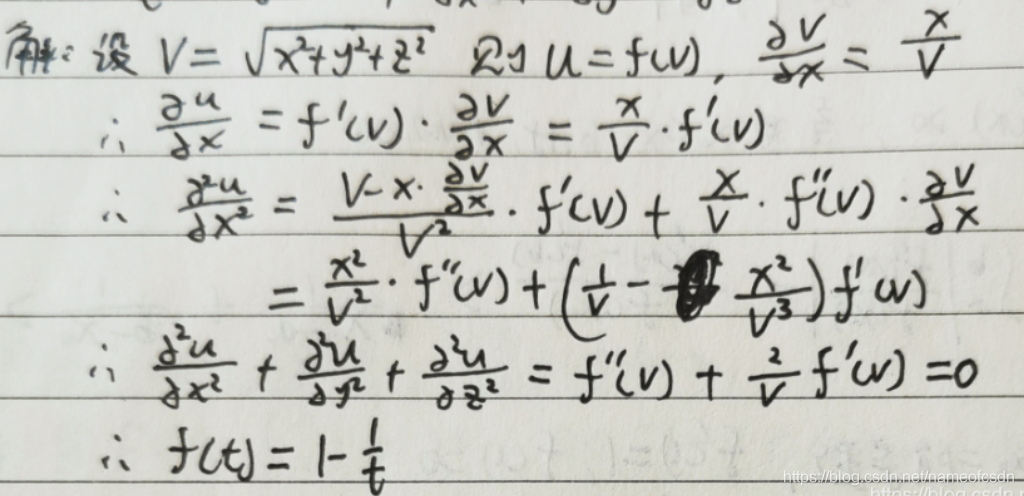
12,设f(x,y)在上有二阶连续偏导,且
,证明:
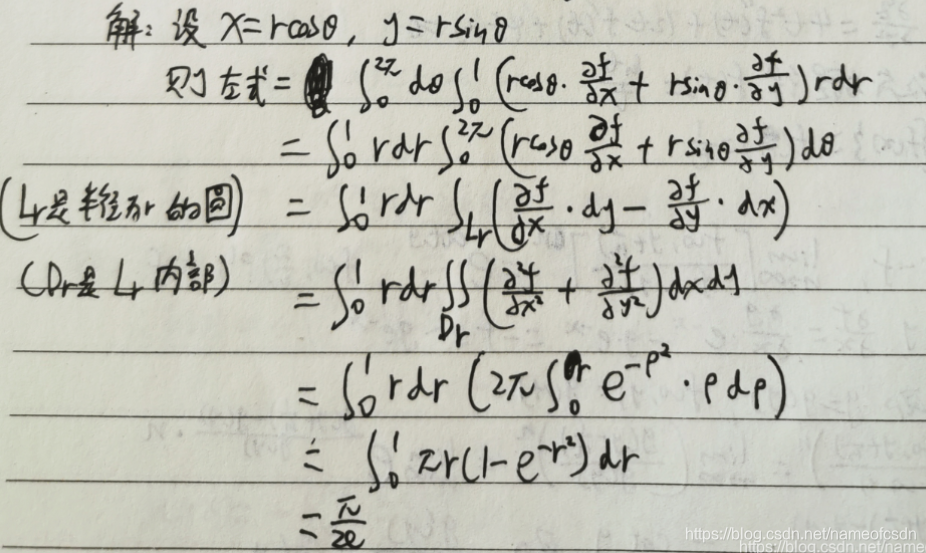
13,,求a和f(x)
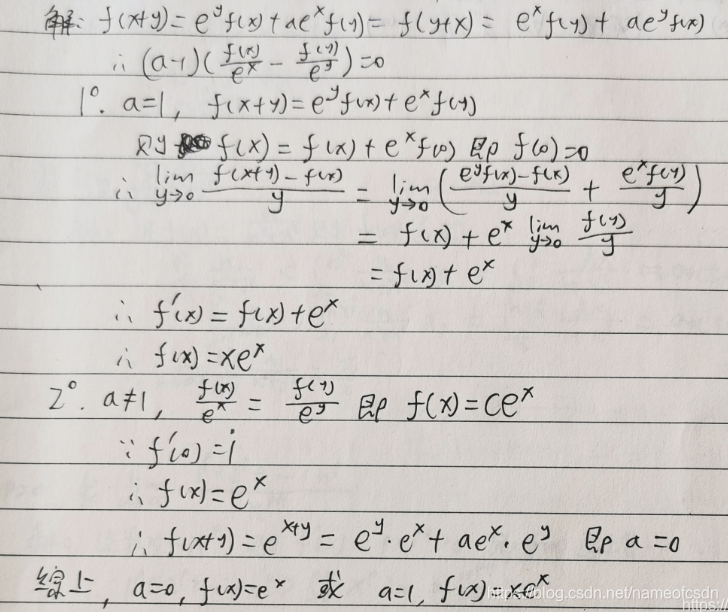
14,f(x)在[0,1]上连续,,求
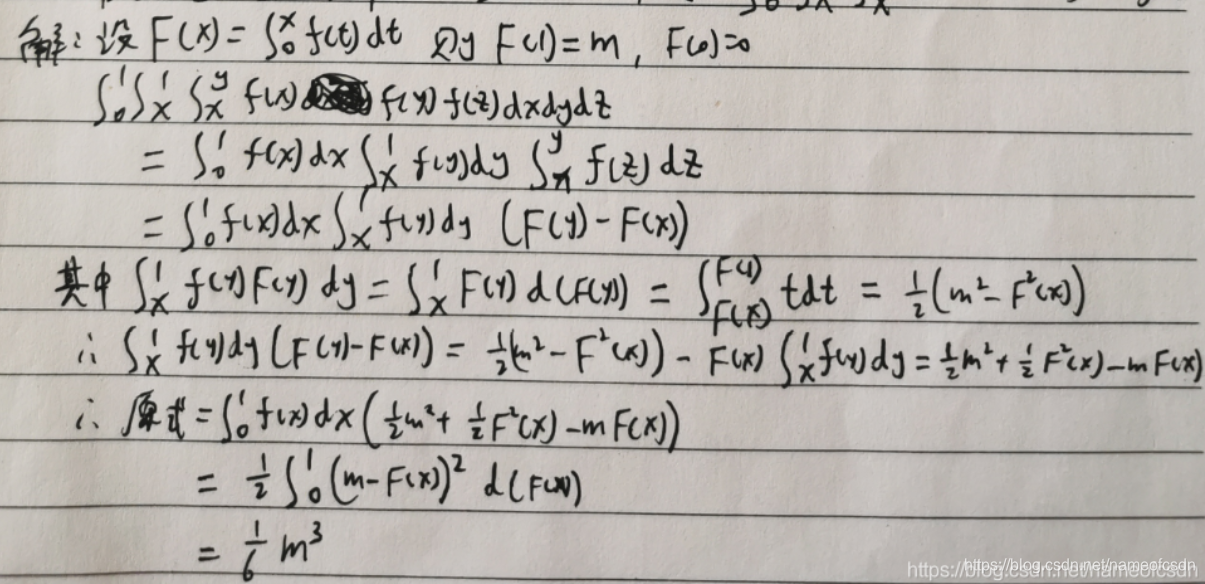
15,设f(x)是具有三阶连续导数的实函数,,证明:
16,满足
,求证
收敛

17,f(x,y)分别关于x,y连续,且关于y单调,证明:f连续
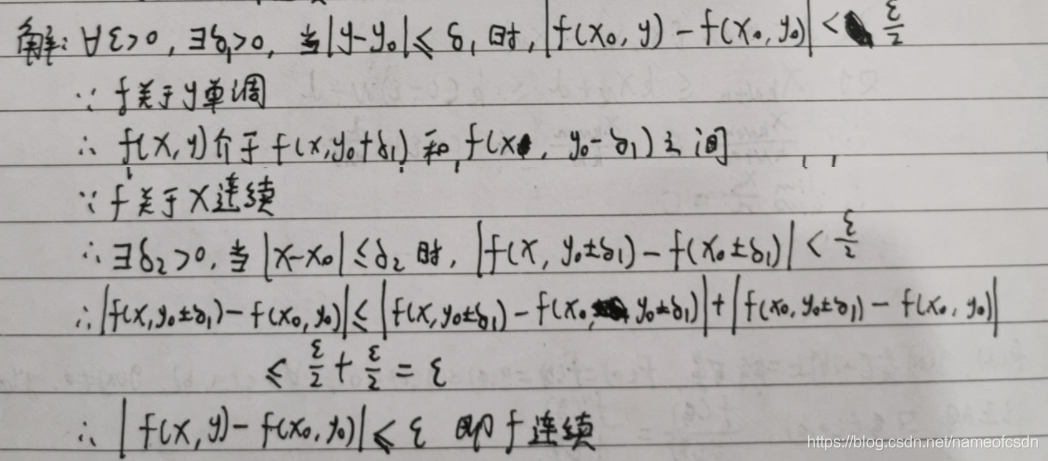
18,f(x)在[a,b]上有连续的导数,f(a)=0,证明

19,f(x)、g(x)均为[a,b]上的连续增函数,证明
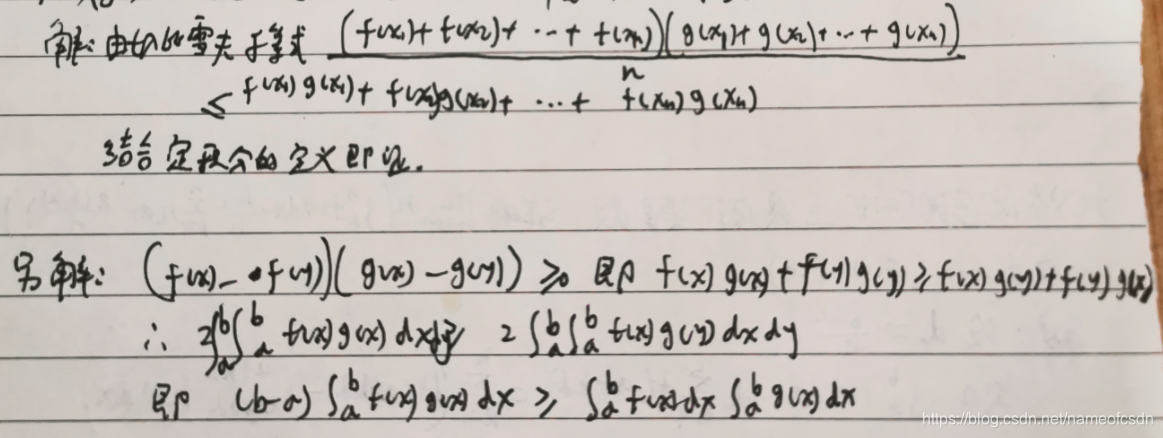
20,设是任意实数,
,求
和

21,(1)若,证明
(2)若存在p为正整数,,证明

22,f(x)在[a,b]上连续,,若f'(a)存在且不为0,求
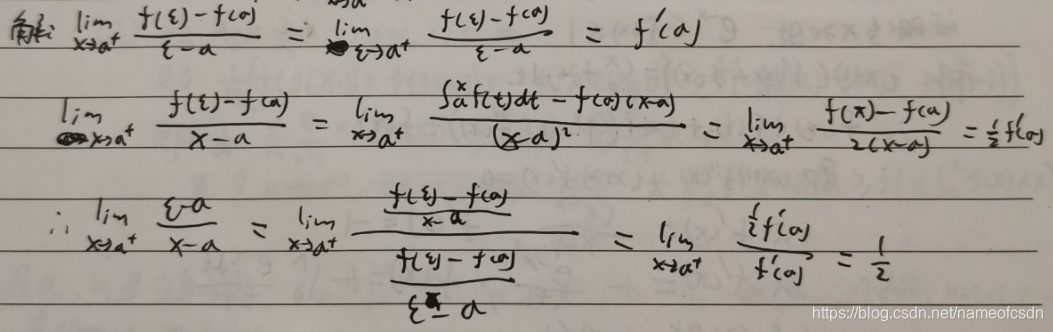
23,f(x)在的邻域内n阶可导,
,
,
证明
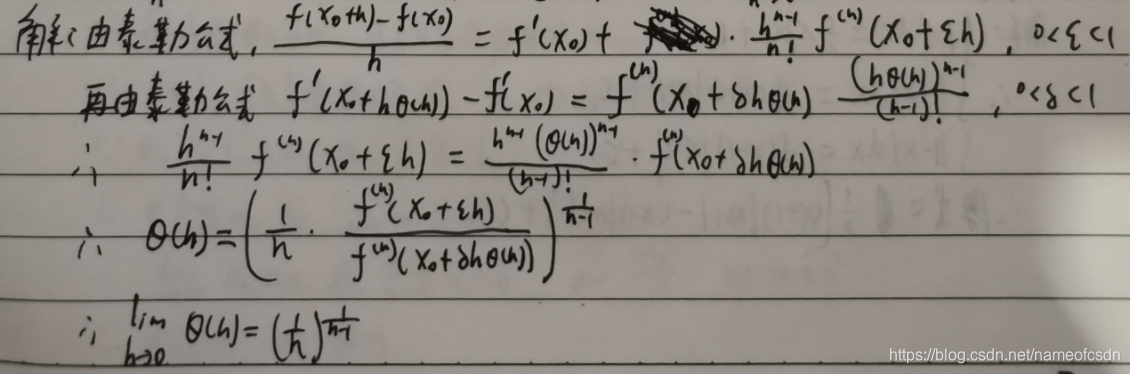
24,,证明f(x)是线性函数

25,当x>-1时,,且f(0)=1,证明x>=0时,
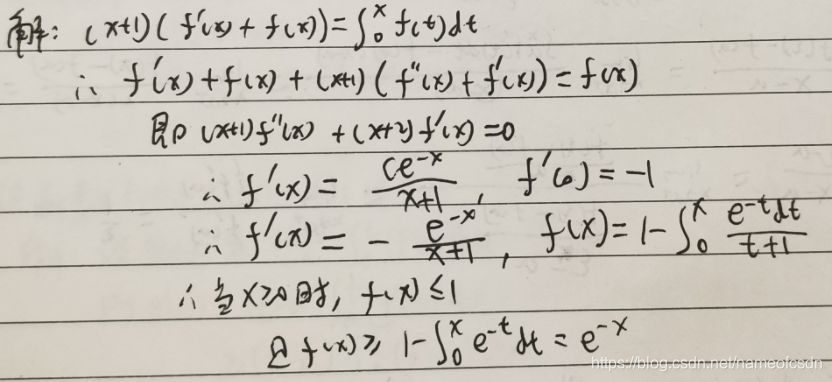
26,求
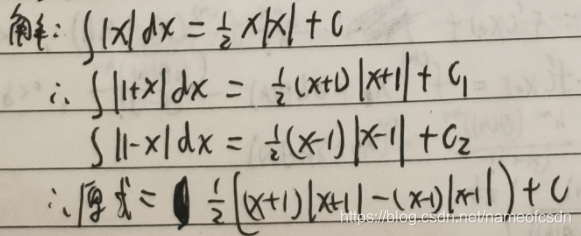
27,f(λx+(1-λ)y)<=λf(x)+(1-λ)f(y), ∀x,y∈R, λ∈(0,1)为常数
(1)证明f(x)连续 (2)∀a>0, ∀g(x)连续,证明





















 9494
9494

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








