python-判断某个坐标点是否在三角形内

主要用到的知识点：

• 在平面直角坐标系内，A（a，b），B（c，d），C（e，f）构成之三角形面积为

   

A，B，C三点最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但只要取绝对值就可以了，不会影响三角形面积的大小。

• 向量积可以被定义为：
  模长：（在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。）
  
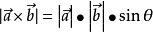  方向：a向量与b向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。（一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从 a以不超过180度的转角转向 b时，竖起的大拇指指向是 c的方向。）
  也可以这样定义（等效）：
  向量积| c|=| a× b|=| a| | b|sin< a,b>
  即 c的长度在数值上等于以 a， b，夹角为θ组成的平行四边形的面积。
  
  
• 利用面积法，如上图所示，如果点P在三角形ABC的内部，则三个小三角形PAB, PBC, PAC的面积之和 = ABC的面积，反之则不相等。
• 
  
• 根据题目要求，设有四个坐标点分别是P（x,y），A（x1,y1）,B（x2,y2）,C（x3,y3）.根据三角形的面积公式可以判断是否构成三角形，即：

  def IsTrangleOrArea(x1,y1,x2,y2,x3,y3):
      return abs((x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)) / 2.0)

  
  
       其次，根据面积公式依次计算PAB,PAC,PBC和ABC的面积 :ABC==PAB+PAC+PBC?。如果成立则说明P点在三角形内部，否则不是
• 详细代码如下，欢迎指正

  #-*- coding: utf8 -*-
  #首先判断是否是三角形
  import math
  corA = raw_input("请输入A点的坐标值:").split(",")
  x1,y1 = int(corA[0]),int(corA[1])
  
  corB = raw_input("请输入B点的坐标值:").split(",")
  x2,y2 = int(corB[0]),int(corB[1])
  
  corC = raw_input("请输入C点的坐标值:").split(",")
  x3,y3 = int(corC[0]),int(corC[1])
  
  corP = raw_input("请输入P点的坐标值:").split(",")
  x,y = int(corP[0]),int(corP[1])
  
  def IsTrangleOrArea(x1,y1,x2,y2,x3,y3):
      return abs((x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)) / 2.0)
  
  def IsInside(x1,y1,x2,y2,x3,y3,x,y):
  
      #三角形ABC的面积
      ABC = IsTrangleOrArea(x1,y1,x2,y2,x3,y3)
  
      # 三角形PBC的面积
      PBC = IsTrangleOrArea(x,y,x2,y2,x3,y3)
  
      # 三角形ABC的面积
      PAC = IsTrangleOrArea(x1,y1,x,y,x3,y3)
  
      # 三角形ABC的面积
      PAB = IsTrangleOrArea(x1,y1,x2,y2,x,y)
  
      return (ABC == PBC + PAC + PAB)
  
  if __name__ =="__main__":
     #if IsInside(10, 30, 20, 0, 10, 30, 10, 15):
     if IsInside(x1,y1,x2,y2,x3,y3,x,y):
        print "Inside"
     else:
        print "Outside"