matlab和Eigen库中的一些旋转矩阵（方向余弦矩阵）、四元数和欧拉角之间的转换和绘图的注意事项

最新推荐文章于 2024-10-29 15:46:50 发布

原创最新推荐文章于 2024-10-29 15:46:50 发布 · 4.6k 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#Eigen #欧拉角 #旋转矩阵 #姿态变换 #matlab

最近用matlab和Eigen库中的一些旋转矩阵（方向余弦矩阵）、四元数和欧拉角之间的转换和绘图，弄得我有些头疼，把遇到的问题记录一下，以防以后又脑阔疼....有不同的理解可以再评论区批评指正～

主要问题有两个

1、matlab工具箱自带的的姿态转换函数定义有歧义（quat2eul（）和quat2angle( )定义不一样），会导致转换出来的欧拉角结果出错；

2、eigen库中使用欧拉角转换eulerAngles（）时，得到的结果每轴相差180度(看起来不太对，其实真正结果时对的)

定义

首先要明确一下欧拉角、旋转矩阵、四元数的在表示旋转时的定义，参考：

https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89%E8%A7%92

https://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5

https://zh.wikipedia.org/wiki/%E5%9B%9B%E5%85%83%E6%95%B8

很可惜地，對於夾角的順序和標記，夾角的兩個軸的指定，並沒有任何常規。科學家對此從未達成共識。每當用到歐拉角時，我們必須明確的表示出夾角的順序，指定其參考軸。

这就是欧拉角很烦人的原因...很多情况下，我感觉在说欧拉角的时候，并没有提到其的旋转轴的顺序，故在画图的时候一般使用欧拉角来表示比较直观，就非常非常的头疼（也可能是我太菜了orz）...

所以，对于姿态表示欧拉角是不唯一的，而旋转矩阵和四元数是唯一的！

欧拉角的表示方式有24种，即2×（3*2*2）种，2代表内旋和外旋，即是固定坐标轴转还是按转动后的坐标轴转的；3代表第一次旋转的3个轴向，接着2代表除了上次的那个轴外的另外两个轴向，还有一个2也是代表除了上次的那个轴外的另外两个轴向。

内旋(intrinsic rotations) = 旋转轴(rotated axis)

外旋(extrinsic rotations) = 固定轴(static/fixed axis)

https://zhuanlan.zhihu.com/p/85108850

所以我们在使用欧拉角转旋转矩阵和四元数的时候，要首先分清时内旋还是外旋，然后在分清其旋转轴向...

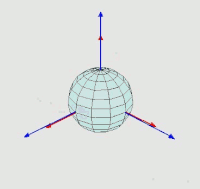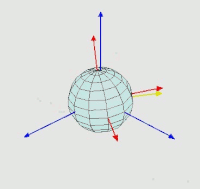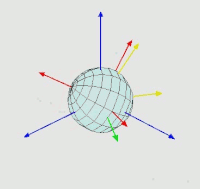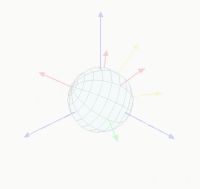
比如该图代表的就是按转动后的坐标轴（蓝色的）计算欧拉角的，即为内旋

在一般的导航定位，比如无人车、无人机等的欧拉角表示，如果没有说明，则很可能是内旋的ZYX顺序。

Matlab函数转换

一般情况下，我们做完位姿解算，会使用matlab画出误差曲线来判断结果是否准确，这个时候一般用欧拉角来绘图比较直观，然而在绘图的时候，有时候会感觉画出来的欧拉角很奇怪，比如欧拉角上下相反...

在MATLAB工具包使用了两种不同的方式来表示四元数，在空航天工具箱中使用的四元数惯例本质上是其机器人学工具箱中使用的四元数惯例的共轭。有关这些区别的更多详细信息，请参见以下链接：

https://ww2.mathworks.cn/matlabcentral/answers/352465-what-is-the-aerospace-blockset-quaternion-convention?s_tid=answers_rc1-2_p2_MLT

https://ww2.mathworks.cn/matlabcentral/answers/465053-rotation-order-of-quatrotate

Robotics Toolbox的是quat2eul( )

Aerospace Toolbox的是quat2angle( )

https://ww2.mathworks.cn/matlabcentral/answers/523677-quat2eul-quat-and-dcm2angle-r-difference-for-zyx-sequence

并且在matlab中，四元数的定义是a+bi+cj+dk，即w、x、y、z.

https://ww2.mathworks.cn/help/robotics/ref/quaternion.html

一般我们定义的四元数是按右手法则的，即拇指朝向旋转轴（xyz的方向），四指指向旋转方向（w代表旋转大小），这和Robotics Toolbox的是quat2eul( ) 的函数是吻合的，而Aerospace Toolbox的是quat2angle( )则是左手法则，故差一个共轭！

这些在使用相应函数时都要注意。

另外，这个工具箱有时候不好安装，要激活matlab的权限，对有的破解版来说比较麻烦，所以我觉得还是直接自己写一个转换代码比较方便T_T

这里代码的定义是一般无人机使用的欧拉角的定义，即内旋的ZYX

function [rpy] = q2euler(q)
% [qx qy qz qw] --> [roll, pitch, yaw] 

	qx = q(1);
	qy = q(2);
	qz = q(3);
    qw = q(4);
	
	roll = atan2(2*(qw*qx+qy*qz), 1-2*(qx*qx+qy*qy));
	pitch = asin(2*(qw*qy-qz*qx));
	yaw = atan2(2*(qw*qz+qx*qy), 1-2*(qy*qy+qz*qz));

    rpy = [roll, pitch, yaw];
end

function [rpy] = c2euler(c)
%UNTITLED2 此处显示有关此函数的摘要
%   此处显示详细说明
    rpy(1) = atan2(c(3,2),c(3,3));
    rpy(2) = atan2(-c(3,1),sqrt(c(3,2)^2+c(3,3)^2));
    rpy(3) = atan2(c(2,1),c(1,1));
end

具体请参考

https://www.cnblogs.com/tiandsp/p/10733607.html

Eigen库转换

在Eigen库中有互相转换的函数，见如下代码示例

旋转矩阵转欧拉角时，若该旋转矩阵是之前由欧拉角转换来的，想得到之前的欧拉角的值，则旋转轴的顺序必须一致，如从ZYX顺序来的，则使用eulerAngles（）是得用ZYX顺序，即（2,1,0），得到的为ypr的值。

注意，Eigen库中eulerAngles（）是默认内旋的方式

* \returns the Euler-angles of the rotation matrix \c *this using the convention defined by the triplet (\a a0,\a a1,\a a2)
  *
  * Each of the three parameters \a a0,\a a1,\a a2 represents the respective rotation axis as an integer in {0,1,2}.
  * For instance, in:
  * \code Vector3f ea = mat.eulerAngles(2, 0, 2); \endcode
  * "2" represents the z axis and "0" the x axis, etc. The returned angles are such that
  * we have the following equality:
  * \code
  * mat == AngleAxisf(ea[0], Vector3f::UnitZ())
  *      * AngleAxisf(ea[1], Vector3f::UnitX())
  *      * AngleAxisf(ea[2], Vector3f::UnitZ()); \endcode
  * This corresponds to the right-multiply conventions (with right hand side frames).
  * 
  * The returned angles are in the ranges [0:pi]x[-pi:pi]x[-pi:pi].

int main(int argc, char **argv)
{
Eigen::Vector3d rpy_raw, ypr;
    rpy_raw << 30, 60, 150;
    rpy_raw = rpy_raw * M_PI / 180;

    Eigen::Matrix3d c;

    //输入部分为YPR,所以转换的输出也是YPR
    c = Eigen::AngleAxisd(rpy_raw[2], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(rpy_raw[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(rpy_raw[0], Eigen::Vector3d::UnitX());
    ypr = c.eulerAngles(2, 1, 0);

    cout << ypr.transpose() * 180 / M_PI << endl;

    return 0;
}

这个是按ZYX转的

下面这个是按照XYZ方式旋转的

//主函数
int main(int argc, char **argv)
{

    Eigen::Vector3d rpy_raw, rpy_1;
    rpy_raw << 30, 60, 150;
    rpy_raw = rpy_raw * M_PI / 180;

    Eigen::Matrix3d c;

    //输入部分为RPY,所以转换的输出也是RPY
    c = Eigen::AngleAxisd(rpy_raw[0], Eigen::Vector3d::UnitX()) * Eigen::AngleAxisd(rpy_raw[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(rpy_raw[2], Eigen::Vector3d::UnitZ());
    // c = Eigen::AngleAxisd(rpy_raw[2], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(rpy_raw[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(rpy_raw[0], Eigen::Vector3d::UnitX());
    rpy_1 = c.eulerAngles(0, 1, 2);

    cout << rpy_1.transpose() * 180 / M_PI << endl;

    return 0;
}

若时四元数的话，只需要先把四元数转成旋转矩阵，再转成欧拉角即可

    Eigen::Quaterniond q;
    Eigen::Matrix3d c;
    c = q.toRotationMatrix();

回到最初的问题，为什么使用eulerAngles（）有时候得到的欧拉角会相差180度

代码如下

int main(int argc, char **argv)
{
    Eigen::Vector3d rpy_raw;
    rpy_raw << -1, 2, 3;
    rpy_raw = rpy_raw * M_PI / 180;

    Eigen::Matrix3d c;
    c = Eigen::AngleAxisd(rpy_raw[2], Eigen::Vector3d::UnitZ()) * Eigen::AngleAxisd(rpy_raw[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(rpy_raw[0], Eigen::Vector3d::UnitX());
    Eigen::Vector3d rpy_tran = c.transpose().eulerAngles(2, 1, 0) / M_PI * 180;
    std::cout << rpy_tran[2] << " " << rpy_tran[1] << " " << rpy_tran[0] << std::endl;

    return 0;

输出结果

-178.896 -178.055 176.964

正确的结果应该时-1,2,3的，我们转换得到的结果貌似每轴和正确结果都相差180度

回到eulerAngles（）定义中去，有一句话

The returned angles are in the ranges [0:pi]x[-pi:pi]x[-pi:pi].

即row的角度范围时【0-180°】，当我们row小于0时，Eigen库会把YZ两轴旋转180度，从而达到让X轴旋转角度大于0°的目的，各位可以试一试按ZYX的方式旋转，将ZY分别旋转180度，原本X为负的旋转角就变成了正的！

这就是Eigen库输出的欧拉角看起来不太对的原因了！其实我们用到欧拉角，主要还是在画图中，比较直观，计算姿态的话直接用旋转矩阵和四元数，就没有这么多麻烦事了～