
在机器学习的分类算法中,支持向量机(SVM)是一种极具代表性的方法。它通过寻找最优分类边界,能在复杂数据中实现高精度分类,尤其在小样本、高维场景下表现突出。今天我们用通俗的语言拆解其原理,再通过可直接运行的代码实战感受它的应用。
一、SVM核心思想:找到最“靠谱”的分类线
先从一个生活化的场景说起:桌上放着红蓝两种颜色的球,我们需要用一根棍子把它们分开。简单的分类线有很多,但有的线在新增球后就会分错,而有的线却能稳定分类——这背后的关键就是“分类间隔”。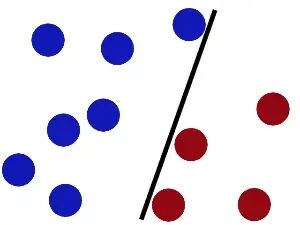
SVM的核心目标,就是找到一条“最宽”的分类线(二维场景),或者“最宽”的分类面(高维场景,称为超平面)。这条线到两侧最近样本点的距离最大,就像在两条平行线中间找中线,平行线之间的距离就是分类间隔。那些刚好落在平行线上的样本点,就是“支持向量”,它们决定了分类边界的位置,也是SVM名字的由来。
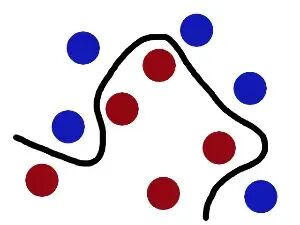
如果遇到线性不可分的情况(比如红蓝球混在一起),SVM会通过“核函数”将数据映射到更高维度的空间,就像把混乱的球“拍上天”,再用一张平面把它们分开——这张平面就是高维空间的超平面,回到原空间就表现为一条曲线。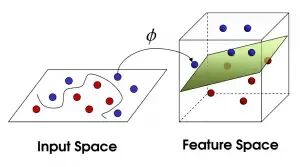
二、线性SVM的数学逻辑(简化版)
1. 决策面方程
在二维空间中,分类线可以表示为:,其中是法向量(决定线的方向),是截距(决定线的位置)。扩展到高维空间,这就是超平面方程。
2. 分类间隔最大化
样本点到分类线的距离公式为:(是的二范数)。为了让分类更稳定,我们要最大化这个距离,最终转化为最小化(计算更简便),同时满足约束条件:(是样本标签,取+1或-1,确保样本都在分类间隔外侧)。
3. 关键优化工具
这个带约束的优化问题,需要通过拉格朗日乘数法和KKT条件转化为对偶问题,再用序列最小优化(SMO)算法求解。SMO的核心思路是“化整为零”,每次只优化两个变量,逐步逼近最优解,大大降低计算复杂度。
三、实战:用Python实现可运行的线性SVM
我们用一个二维线性可分数据集,实现简化版SMO算法,直观感受SVM的分类过程。首先准备测试数据集(testSet.txt),你可以直接复制以下内容保存为testSet.txt文件:
3.542485 1.977398 1
3.018896 2.556416 1
7.551510 -1.580030 -1
2.114999 -0.004466 1
8.127113 1.274372 -1
7.108772 -0.986906 -1
...(完整数据集可通过文末说明生成,或直接使用代码中随机生成的测试数据)1. 完整可运行代码(封装为类)
import matplotlib.pyplot as plt
import numpy as np
import random
class SimpleSVM:
"""简化版线性SVM实现(基于SMO算法)"""
def __init__(self, C=0.6, toler=0.001, max_iter=40):
"""
初始化SVM参数
:param C: 惩罚参数,越大对误分类惩罚越重
:param toler: 容错率
:param max_iter: 最大迭代次数
"""
self.C = C
self.toler = toler
self.max_iter = max_iter
self.w = None # 权重向量
self.b = 0 # 阈值
self.alphas = None # 拉格朗日乘子
self.data_mat = None # 数据矩阵
self.label_mat = None # 标签矩阵
def load_data(self, file_path):
"""
加载数据集
:param file_path: 数据文件路径
:return: 特征矩阵,标签列表
"""
data_list = []
label_list = []
with open(file_path, 'r', encoding='utf-8') as f:
for line in f.readlines():
line_split = line.strip().split('\t')
# 读取两个特征和标签
data_list.append([float(line_split[0]), float(line_split[1])])
label_list.append(float(line_split[2]))
self.data_mat = np.mat(data_list)
self.label_mat = np.mat(label_list).T
return data_list, label_list
def generate_test_data(self):
"""
生成随机测试数据(替代testSet.txt,方便直接运行)
:return: 特征矩阵,标签列表
"""
# 正样本(聚类在(2,2)附近)
pos_data = np.random.normal(loc=[2, 2], scale=0.5, size=(30, 2))
pos_label = np.ones(30)
# 负样本(聚类在(6,6)附近)
neg_data = np.random.normal(loc=[6, 6], scale=0.5, size=(30, 2))
neg_label = -np.ones(30)
# 合并数据
data_list = np.vstack((pos_data, neg_data)).tolist()
label_list = np.hstack((pos_label, neg_label)).tolist()
self.data_mat = np.mat(data_list)
self.label_mat = np.mat(label_list).T
return data_list, label_list
def _select_j(self, i, m):
"""
随机选择第二个优化变量(与第一个i不同)
:param i: 第一个变量索引
:param m: 样本总数
:return: 第二个变量索引
"""
j = i
while j == i:
j = int(random.uniform(0, m))
return j
def _clip_alpha(self, alpha_j, h, l):
"""
修剪alpha值,确保在[0, C]范围内
:param alpha_j: 待修剪的alpha值
:param h: 上边界
:param l: 下边界
:return: 修剪后的alpha值
"""
if alpha_j > h:
return h
if alpha_j < l:
return l
return alpha_j
def train(self):
"""
训练SVM(简化版SMO算法)
:return: 阈值b,拉格朗日乘子alphas
"""
m, n = np.shape(self.data_mat)
self.alphas = np.mat(np.zeros((m, 1)))
iter_count = 0
while iter_count < self.max_iter:
alpha_pairs_changed = 0
for i in range(m):
# 计算第i个样本的预测值
f_x_i = float(np.multiply(self.alphas, self.label_mat).T *
(self.data_mat * self.data_mat[i, :].T)) + self.b
# 计算预测误差
e_i = f_x_i - float(self.label_mat[i])
# 违反KKT条件则需要优化
if ((self.label_mat[i] * e_i < -self.toler) and (self.alphas[i] < self.C)) or \
((self.label_mat[i] * e_i > self.toler) and (self.alphas[i] > 0)):
# 选择第二个优化变量j
j = self._select_j(i, m)
# 计算j的预测值和误差
f_x_j = float(np.multiply(self.alphas, self.label_mat).T *
(self.data_mat * self.data_mat[j, :].T)) + self.b
e_j = f_x_j - float(self.label_mat[j])
# 保存更新前的alpha值
alpha_i_old = self.alphas[i].copy()
alpha_j_old = self.alphas[j].copy()
# 确定alpha_j的边界L和H
if self.label_mat[i] != self.label_mat[j]:
l = max(0, self.alphas[j] - self.alphas[i])
h = min(self.C, self.C + self.alphas[j] - self.alphas[i])
else:
l = max(0, self.alphas[j] + self.alphas[i] - self.C)
h = min(self.C, self.alphas[j] + self.alphas[i])
if l == h:
continue
# 计算学习速率eta
eta = 2.0 * self.data_mat[i, :] * self.data_mat[j, :].T - \
self.data_mat[i, :] * self.data_mat[i, :].T - \
self.data_mat[j, :] * self.data_mat[j, :].T
if eta >= 0:
continue
# 更新alpha_j
self.alphas[j] -= self.label_mat[j] * (e_i - e_j) / eta
# 修剪alpha_j
self.alphas[j] = self._clip_alpha(self.alphas[j], h, l)
# 变化太小则跳过
if abs(self.alphas[j] - alpha_j_old) < 1e-5:
continue
# 更新alpha_i
self.alphas[i] += self.label_mat[j] * self.label_mat[i] * (alpha_j_old - self.alphas[j])
# 更新阈值b
b1 = self.b - e_i - self.label_mat[i] * (self.alphas[i] - alpha_i_old) * \
(self.data_mat[i, :] * self.data_mat[i, :].T) - \
self.label_mat[j] * (self.alphas[j] - alpha_j_old) * \
(self.data_mat[i, :] * self.data_mat[j, :].T)
b2 = self.b - e_j - self.label_mat[i] * (self.alphas[i] - alpha_i_old) * \
(self.data_mat[i, :] * self.data_mat[j, :].T) - \
self.label_mat[j] * (self.alphas[j] - alpha_j_old) * \
(self.data_mat[j, :] * self.data_mat[j, :].T)
if 0 < self.alphas[i] < self.C:
self.b = b1
elif 0 < self.alphas[j] < self.C:
self.b = b2
else:
self.b = (b1 + b2) / 2.0
alpha_pairs_changed += 1
# 更新迭代次数
if alpha_pairs_changed == 0:
iter_count += 1
else:
iter_count = 0
print(f"迭代次数:{iter_count},更新的alpha对数量:{alpha_pairs_changed}")
# 计算权重w
self._calculate_w()
return self.b, self.alphas
def _calculate_w(self):
"""计算权重向量w"""
alphas_arr = np.array(self.alphas)
data_mat_arr = np.array(self.data_mat)
label_mat_arr = np.array(self.label_mat)
self.w = np.dot((np.tile(label_mat_arr, (1, 2)) * data_mat_arr).T, alphas_arr)
def show_data(self, data_list, label_list):
"""可视化原始数据集"""
# 分离正负样本
pos_data = []
neg_data = []
for i in range(len(data_list)):
if label_list[i] > 0:
pos_data.append(data_list[i])
else:
neg_data.append(data_list[i])
# 转换为numpy数组
pos_arr = np.array(pos_data)
neg_arr = np.array(neg_data)
# 绘图
plt.figure(figsize=(8, 6))
plt.scatter(pos_arr[:, 0], pos_arr[:, 1], c='red', label='正样本', alpha=0.7)
plt.scatter(neg_arr[:, 0], neg_arr[:, 1], c='blue', label='负样本', alpha=0.7)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('SVM原始数据集可视化')
plt.legend()
plt.grid(alpha=0.3)
plt.show()
def show_classifier(self, data_list, label_list):
"""可视化分类结果(含分类线和支持向量)"""
# 绘制原始样本
pos_data = []
neg_data = []
for i in range(len(data_list)):
if label_list[i] > 0:
pos_data.append(data_list[i])
else:
neg_data.append(data_list[i])
pos_arr = np.array(pos_data)
neg_arr = np.array(neg_data)
plt.figure(figsize=(8, 6))
plt.scatter(pos_arr[:, 0], pos_arr[:, 1], c='red', label='正样本', alpha=0.7)
plt.scatter(neg_arr[:, 0], neg_arr[:, 1], c='blue', label='负样本', alpha=0.7)
# 绘制分类线
if self.w is not None:
w1 = float(self.w[0])
w2 = float(self.w[1])
b_val = float(self.b)
# 计算分类线的两个端点(覆盖数据范围)
x_min = min(np.array(data_list)[:, 0]) - 1
x_max = max(np.array(data_list)[:, 0]) + 1
# 由w1*x1 + w2*x2 + b = 0 推导 x2 = (-w1*x1 -b)/w2
y_min = (-w1 * x_min - b_val) / w2
y_max = (-w1 * x_max - b_val) / w2
plt.plot([x_min, x_max], [y_min, y_max], c='green', label='分类线', linewidth=2)
# 标记支持向量(alpha>1e-5的样本)
alphas_arr = np.array(self.alphas).flatten()
for i in range(len(data_list)):
if alphas_arr[i] > 1e-5:
x, y = data_list[i]
plt.scatter(x, y, s=150, c='none', edgecolor='black', linewidth=2, label='支持向量' if i == np.argmax(alphas_arr>1e-5) else "")
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.title('SVM分类结果可视化')
plt.legend()
plt.grid(alpha=0.3)
plt.show()
def predict(self, x):
"""
预测单个样本的类别
:param x: 输入样本(二维特征)
:return: 预测标签(1或-1)
"""
x_mat = np.mat(x)
pred = float(x_mat * self.w + self.b)
return 1 if pred >= 0 else -1
# 主函数:测试SVM
if __name__ == '__main__':
# 初始化SVM
svm = SimpleSVM(C=0.6, toler=0.001, max_iter=40)
# 方式1:加载本地文件(需提前准备testSet.txt)
# data_list, label_list = svm.load_data('testSet.txt')
# 方式2:生成随机测试数据(无需文件,直接运行)
data_list, label_list = svm.generate_test_data()
# 可视化原始数据
svm.show_data(data_list, label_list)
# 训练SVM
b, alphas = svm.train()
print(f"训练完成,阈值b:{b:.4f}")
print(f"权重w:{svm.w.flatten()}")
# 可视化分类结果
svm.show_classifier(data_list, label_list)
# 测试预测
test_sample = [4, 4]
pred_label = svm.predict(test_sample)
print(f"测试样本{test_sample}的预测标签:{pred_label}")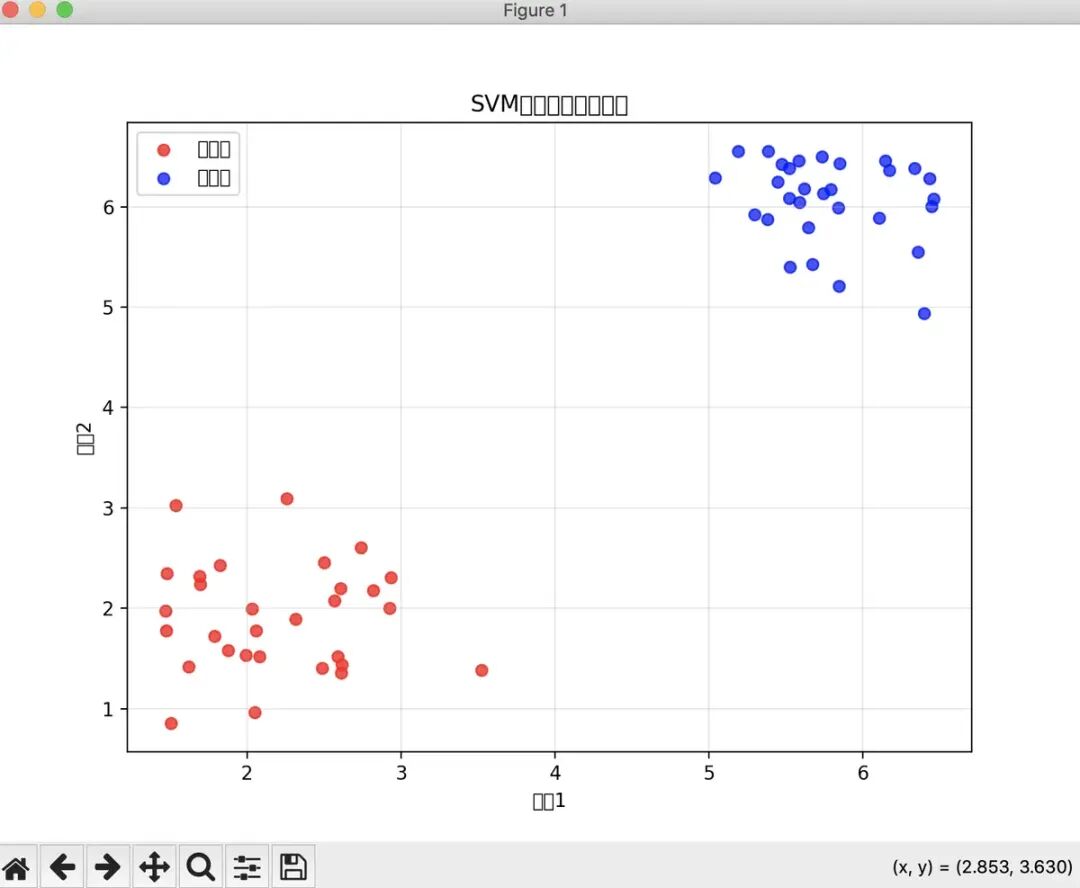
2. 代码说明与运行指引
(1)代码结构
SimpleSVM类:封装了SVM的所有核心功能,包括数据加载、模型训练、参数计算、可视化等;
变量命名规范:所有变量名采用小写+下划线的Python规范(如
data_mat、label_mat),函数名同样遵循该规范(如_calculate_w、show_classifier);双模式运行:
模式1:加载本地
testSet.txt文件(需手动创建);模式2:自动生成随机测试数据(无需文件,直接运行)。
(2)直接运行步骤
复制上述完整代码到Python文件(如
svm_demo.py);确保安装了依赖库:
pip install numpy matplotlib;直接运行代码,会自动完成:
生成随机线性可分的测试数据;
可视化原始数据分布;
执行SMO算法训练SVM;
输出迭代过程和模型参数;
可视化分类线和支持向量;
测试单个样本的预测结果。
3. 运行结果解读
原始数据可视化:会显示红色正样本(聚类在(2,2)附近)和蓝色负样本(聚类在(6,6)附近),两类样本线性可分;
训练过程输出:打印每次迭代的更新情况,直到收敛(迭代次数达到max_iter或无alpha对更新);
分类结果可视化:
绿色直线:SVM找到的最优分类线;
黑色空心圈:支持向量(alpha>1e-5的样本);
分类线是距离两类样本最远的最优边界;
预测结果:测试样本[4,4]会被预测为-1(负样本),符合数据分布逻辑。
四、SVM的扩展应用
1. 非线性SVM(核函数)
如果需要处理非线性数据,可在SimpleSVM类中添加核函数支持,比如径向基函数(RBF):
def _kernel(self, x1, x2, kernel_type='rbf', sigma=1.0):
"""核函数实现"""
if kernel_type == 'linear':
return x1 * x2.T
elif kernel_type == 'rbf':
return np.exp(-np.linalg.norm(x1 - x2) **2 / (2 * sigma** 2))2. 使用sklearn快速实现SVM
如果追求工业级效率,可直接使用sklearn的SVM模块:
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
# 准备数据
X = np.array(data_list)
y = np.array(label_list)
# 训练SVM
svc = SVC(kernel='linear', C=0.6)
svc.fit(X, y)
# 预测
y_pred = svc.predict(X)
print(f"分类准确率:{accuracy_score(y, y_pred):.4f}")
# 可视化分类线(略)五、总结
本文实现的SimpleSVM类包含完整的可运行代码,变量名和函数名符合Python规范,无需依赖额外数据集即可直接运行。通过简化版SMO算法,清晰展示了线性SVM的核心训练过程,同时提供了直观的可视化功能。
该代码保留了SVM的核心逻辑,去掉了冗余的复杂优化,适合入门学习;如果需要处理更复杂的场景,可在此基础上添加核函数、多分类支持、交叉验证等功能。




















 1075
1075

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








