匹配类算法纠偏

最近学到位置配准，上次说到了SGVision匹配类中几个算法的应用，只是觉得功能非常的惊喜。各个算法工具应用时检测产品的角度和检测时间都有很大的不同，具体根据检测要求选择算法工具。

虽然会用工具了但是没有深入地思考了解匹配类算法到底是什么，其实匹配类算法的最主要目的就是纠偏。

每一个产品成像的位置都不相同，要实现检测，要先纠偏。

匹配类算法纠偏的原理是：不管产品在图片的哪个位置，都把它固定到一个地方。

以纠偏过来的图片为匹配源，来进行它的检测。比如线间距检测、点间距检测、半径检测等等。

给大家看看下面这张图，就能清晰的看出来不管产品的位置怎么变换能找到并检测距离。

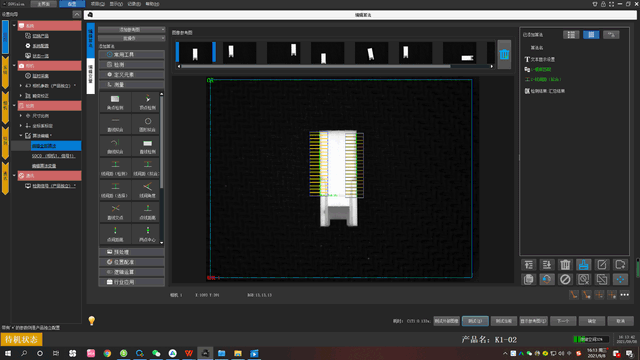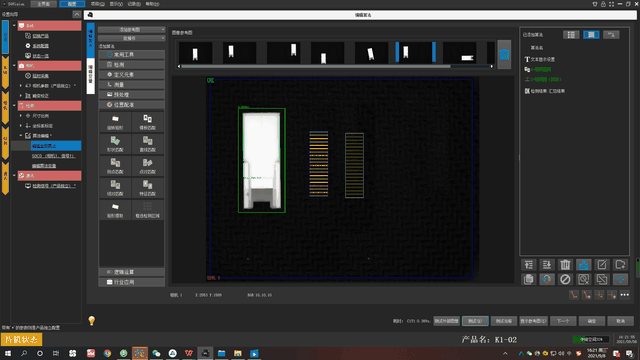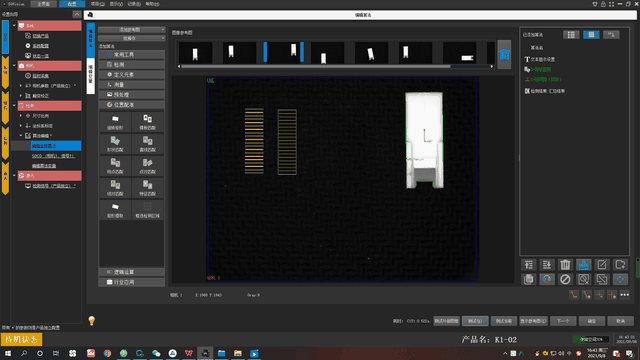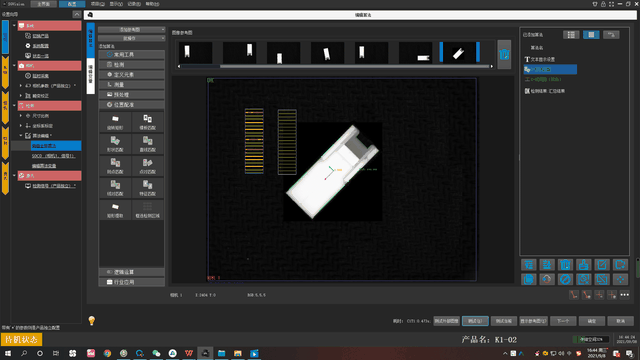
SGVision软件所在的马克拉伯MookLab平台提供视频教程、使用手册、应用案例等学习资料，并且在使用软件过程中遇到任何问题都可咨询，会有专业团队提供线上技术支持、远程协助，帮助每一位用户应用软件去构建视觉项目。