【控制理论】#2 状态空间方程与相轨迹分析

状态空间方程

状态空间方程是现代控制理论的基础，它以矩阵的形式，用一系列一阶微分方程表达系统状态变量、输入及输出之间的关系。

高阶微分方程

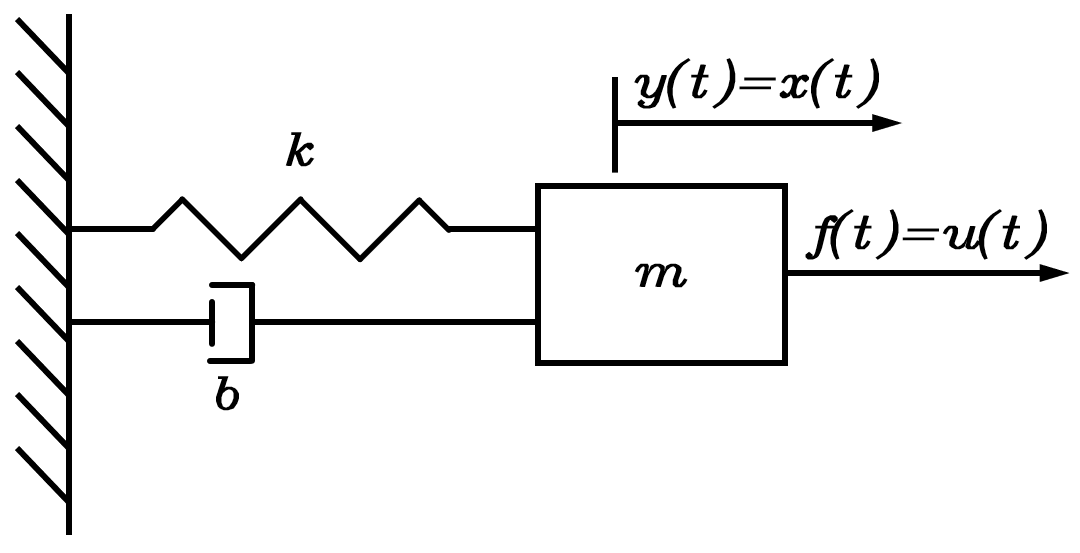
状态空间方程可以将高阶微分方程转化为一阶微分方程组。考虑上图所示的弹簧质量阻尼系统，它的动态微分方程为

$$m\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}+b\frac{\mathrm{d}x(t)}{\mathrm{d}t}+kx(t)=f(t)$$

其中$x(t)$是位移（方向向右），$m$是质量，$b$是阻尼系数，$k$是弹簧系数，$f(t)$是外力。令系统的输入等于外力$u(t)=f(t)$，输出等于位移$y(t)=x(t)$，则通过拉普拉斯变换可得系统的传递函数为

$$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{m{s}^2+bs+k}$$

在现代控制理论中，我们用状态空间方程的表达方式。令输出量及微分方程中最高阶导数以下的各阶导数为状态变量

$$\begin{array}{rl}& z_1(t)=x(t)\\ & z_2(t)=\frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t}=\frac{\mathrm{d}x(t)}{\mathrm{d}t}\end{array}$$

取$z_2(t)$对时间$t$的导数，结合系统的微分方程并代入$u(t)=f(t)$有

$$\begin{array}{rl}\frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}& =\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}=\frac{1}{m}\left(f(t)-b\frac{\mathrm{d}x(t)}{\mathrm{d}t}-kx(t)\right)\\ & =\frac{1}{m}u(t)-\frac{b}{m}{z}_2(t)-\frac{k}{m}{z}_1(t)\end{array}$$

现在我们得到了一阶微分方程组

$$\{\begin{array}{rl}& \frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t}=z_2(t)\\ & \frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}=\frac{1}{m}u(t)-\frac{b}{m}{z}_2(t)-\frac{k}{m}{z}_1(t)\end{array}$$

将上式写成紧凑的矩阵表达形式可得

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -\frac{k}{m}& -\frac{b}{m}\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]+\left[\begin{array}{c}0\\ \frac{1}{m}\end{array}\right][u(t)]$$

系统的输出$y(t)=x(t)$也可以写成矩阵形式

$$y(t)=\left[\begin{array}{cc}1& 0\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]+[0][u(t)]$$

上述形式可推广并得到状态空间方程的一般形式

$$\begin{array}{c}\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\mathbf{Az}(t)+\mathbf{Bu}(t)\\ \mathbf{y}(t)=\mathbf{Cz}(t)+\mathbf{Du}(t)\end{array}$$

符号	名称	维度
$\mathbf{z}(t)$	状态变量	$n\times 1$
$\mathbf{y}(t)$	系统输出	$m\times 1$
$\mathbf{u}(t)$	系统输入	$p\times 1$
$\mathbf{A}$	状态矩阵	$n\times n$
$\mathbf{B}$	输入矩阵	$n\times p$
$\mathbf{C}$	输出矩阵	$m\times n$
$\mathbf{D}$	直接传递矩阵	$m\times p$

状态空间方程与传递函数的关系

上述单输入单输出系统可以同时用传递函数和状态空间方程表示，下面讨论这两种形式之间的关系。

对状态空间方程的一般形式两边进行拉普拉斯变换

$$\begin{array}{c}\mathcal{L}\left[\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}\right]=\mathcal{L}[\mathbf{Az}(t)+\mathbf{Bu}(t)]\\ \mathcal{L}[\mathbf{y}(t)]=\mathcal{L}[\mathbf{Cz}(t)+\mathbf{Du}(t)]\end{array}$$

对于零初始状态，上式可整理为

$$\begin{array}{c}s\mathbf{Z}(s)=\mathbf{AZ}(s)+\mathbf{BU}(s)①\\ \mathbf{Y}(s)=\mathbf{CZ}(s)+\mathbf{DU}(s)②\end{array}$$

其中$\mathbf{Z}(s)=\mathcal{L}[\mathbf{z}(t)],\mathbf{Y}(s)=\mathcal{L}[\mathbf{y}(t)],\mathbf{U}(s)=\mathcal{L}[\mathbf{u}(t)]$。式①调整后得

$$\mathbf{Z}(s)=(s\mathbf{I}-\mathbf{A}{)}^{-1}\mathbf{BU}(s)$$

将其代入式②得

$$\mathbf{Y}(s)=(\mathbf{C}(s\mathbf{I}-\mathbf{A}{)}^{-1}\mathbf{B}+\mathbf{D})\mathbf{U}(s)$$

因此系统的传递函数可以写为

$$G(s)=\frac{\mathbf{Y}(s)}{\mathbf{U}(s)}=\mathbf{C}(s\mathbf{I}-\mathbf{A}{)}^{-1}\mathbf{B}+\mathbf{D}=\frac{\mathbf{C}(s\mathbf{I}-\mathbf{A}{)}^{\ast }\mathbf{B}+|s\mathbf{I}-\mathbf{A}|\mathbf{D}}{|s\mathbf{I}-\mathbf{A}|}$$

写成分数形式后，$|s\mathbf{I}-\mathbf{A}|=0$得出的$s$即为该传递函数的极点，同时根据该方程的定义，$s$也是矩阵$\mathbf{A}$的特征值，因此可通过分析矩阵$\mathbf{A}$的特征值判断系统的表现。

多输入多输出系统

状态空间方程还可用于表示表示多输入多输出系统，以下面这个电路网络为例，该系统有两个输入$\mathbf{u}(t)=[e_1(t),e_2(t){]}^{\top }$和两个输出$\mathbf{y}(t)=[i_1(t),e_{R_3}(t){]}^{\top }$

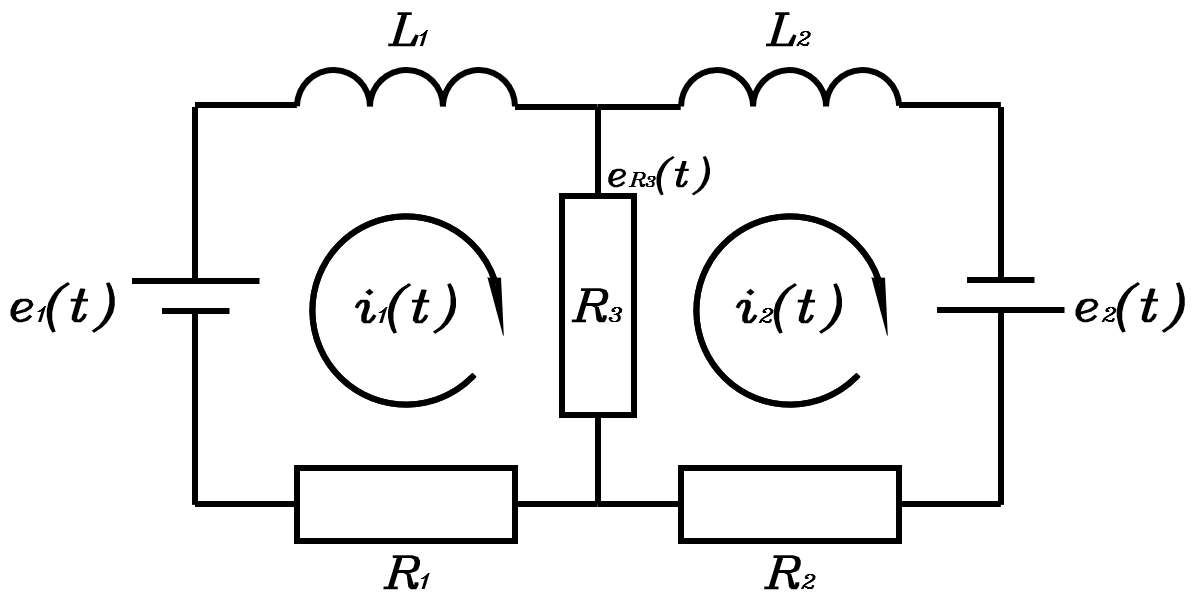
对闭合回路1和2应用基尔霍夫电压定律，我们可以分别列出其动态微分方程

$$\begin{array}{c}{L}_1\frac{\mathrm{d}{i}_1(t)}{\mathrm{d}t}+i_1(t)R_1+e_{R_3}(t)=e_1(t)\\ L_2\frac{\mathrm{d}{i}_2(t)}{\mathrm{d}t}+i_2(t)R_2-e_{R_3}(t)=e_2(t)\end{array}$$

其中$e_{R_3}(t)=(i_1(t)-t_2(t))R_3$，代入调整后得到

$$\begin{array}{c}{L}_1\frac{\mathrm{d}{i}_1(t)}{\mathrm{d}t}+i_1(t)(R_1+R_3)-i_2(t)R_3=e_1(t)\\ L_2\frac{\mathrm{d}{i}_2(t)}{\mathrm{d}t}+i_2(t)(R_2+R_3)-i_1(t)R_3=e_2(t)\end{array}$$

选取系统的输入量作为状态变量

$$\begin{array}{c}{z}_1(t)=i_1(t)\\ z_2(t)=i_2(t)\end{array}$$

并代入调整后得到

$$\begin{array}{c}\frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t}=-\frac{R_1+R_3}{L_1}{z}_1(t)+\frac{R_3}{L_1}{z}_2(t)+\frac{1}{L_1}{e}_1(t)\\ \frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}=\frac{R_3}{L_2}{z}_1(t)-\frac{R_2+R_3}{L_2}{z}_2(t)+\frac{1}{L_2}{e}_2(t)\end{array}$$

将上式写成矩阵形式有

$$\left[\begin{array}{c}\frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t}\\ \frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}\end{array}\right]=\left[\begin{array}{cc}-\frac{R_1+R_3}{L_1}& \frac{R_3}{L_1}\\ \frac{R_3}{L_2}& -\frac{R_2+R_3}{L_2}\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L_1}& 0\\ 0& \frac{1}{L_2}\end{array}\right]\left[\begin{array}{c}{e}_1(t)\\ e_2(t)\end{array}\right]$$

同理系统输出可以写为

$$\mathbf{y}(t)=\left[\begin{array}{c}{i}_1(t)\\ e_{R_3}(t)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ R_3& -R_3\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{e}_1(t)\\ e_2(t)\end{array}\right]$$

相平面与相轨迹分析

相平面与相轨迹使用直观的图形来分析微分方程。相轨迹描述了系统在没有输入影响的情况下，状态变量随时间在相平面上变化的轨迹。

一维相轨迹

首先讨论一阶微分方程的分析方法，考虑如下方程

$$\frac{\mathrm{d}z(t)}{\mathrm{d}t}=z^2(t)-1$$

以$z(t)$为横轴，$\frac{\mathrm{d}z(t)}{\mathrm{d}t}$为纵轴，可绘制出一条抛物线

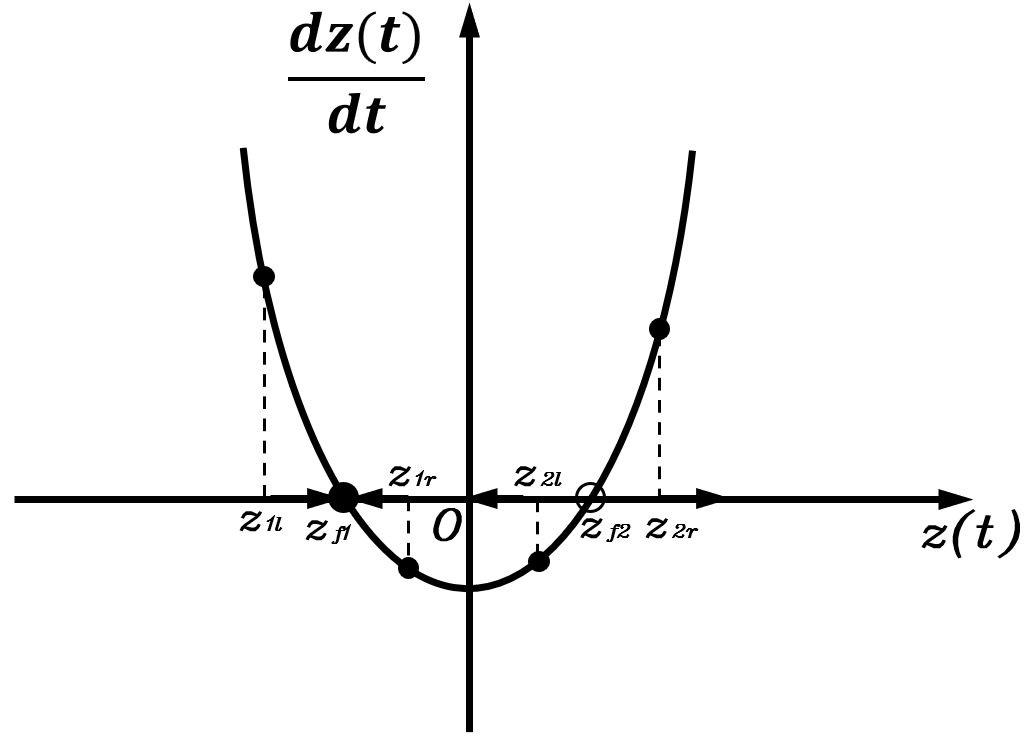
在该相平面中，位于横轴上方的点$\frac{\mathrm{d}z(t)}{\mathrm{d}t}>0$，$z(t)$将随时间向右变化；位于横轴下方的点$\frac{\mathrm{d}z(t)}{\mathrm{d}t}<0$，$z(t)$将随时间向左变化。其中$z_{f1}$和$z_{f2}$是抛物线与横轴的交点，$\frac{\mathrm{d}z(t)}{\mathrm{d}t}=0$，此时$z(t)$不会发生改变，因此这两个点被称为平衡点。

当状态变量小范围偏离平衡点$z_{f1}$时，无论其位于$z_{f1}$左侧还是右侧，都将随时间回到$z_{f1}$，因此$z_{f1}$是稳定平衡点；而当状态变量小范围偏离平衡点$z_{f2}$时，无论其位于$z_{f2}$左侧还是右侧，都无法随时间回到$z_{f2}$，因此$z_{f2}$是不稳定平衡点。

只有在$z(0)<z_{f2}$时，状态变量才会回到平衡点$z_{f1}$，因此$z_{f1}$是一个局部稳定的平衡点。

二维相轨迹

对于一个二维系统，在没有输入的情况下，其状态空间方程为

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]$$

其平衡点位于$z_1(t)=z_2(t)=0$处。

简化形式

若$a_{12},a_{21}\ne 0$，则$\frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t},\frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}$均由$z_1(t),z_2(t)$共同影响，即两个状态变量是耦合的，不易进行分析，因此先考虑$a_{12}=a_{21}=0$的简化形式，即

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]=\left[\begin{array}{cc}{a}_{11}& 0\\ 0& a_{22}\end{array}\right]\left[\begin{array}{c}{z}_1(t)\\ z_2(t)\end{array}\right]$$

下面根据$a_{11}$和$a_{22}$的符号进行分类讨论

情况一：$a_{11},a_{22}>0$

此时$z_1(t),z_2(t)$与其各自的导数同号，即状态变量为正则朝正方向增长，为负则朝负方向增长，平衡点之外的点均随时间远离平衡点，因此该平衡点为不稳定节点。

如果$a_{11}=a_{22}$，则相轨迹呈均匀发散的射线状

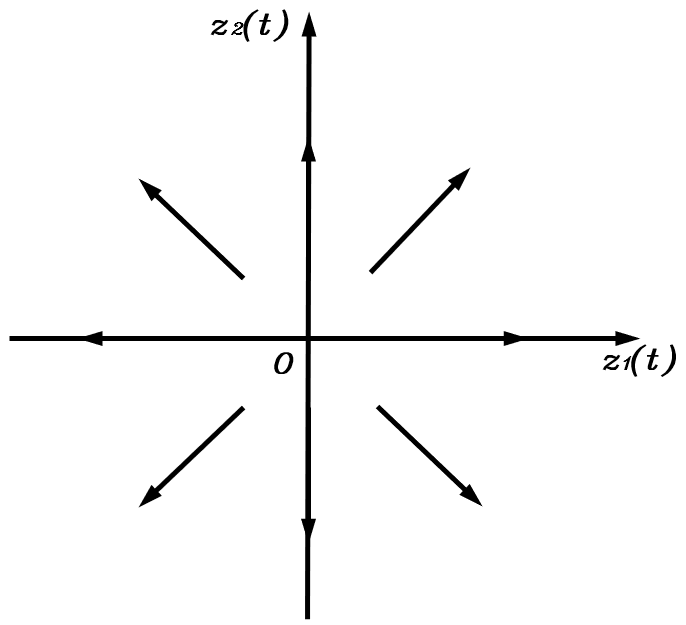
如果$a_{11}\ne a_{22}$，则坐标轴外的相轨迹以曲线朝状态变量变化速率大的方向弯曲

情况二：$a_{11}>0$且$a_{22}<0$

此时$z_1(t)$变化方向与符号相同，而$z_2(t)$变化方向与符号相反，即在平衡点之外，$z_1(t)$趋于无穷，$z_2(t)$趋于零，因此相轨迹会沿着横轴远离平衡点，而沿着纵轴靠近平衡点

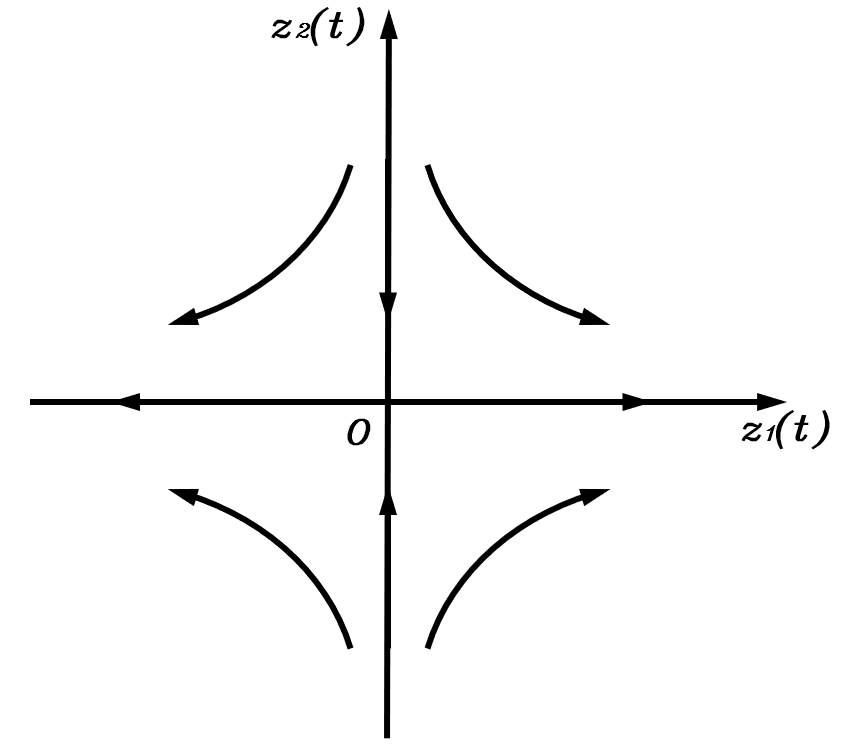
这种仅在一个维度上偏移后会收敛回原平衡点的平衡点称为鞍点，是一个不稳定的点。

$a_{11}<0$且$a_{22}>0$的情况与之类似，不再赘述。

情况三：$a_{11},a_{22}<0$

与情况一的分析类似，其相轨迹如下图所示

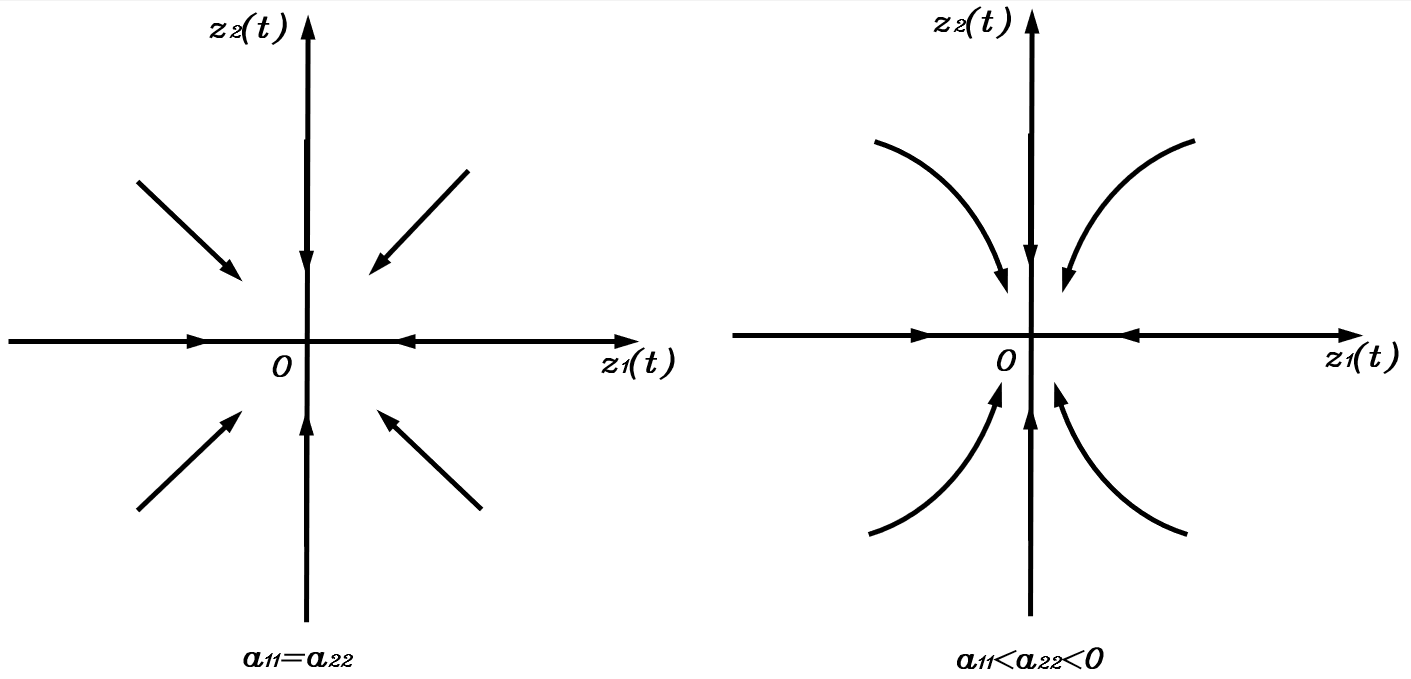
这种情况下，该平衡点为稳定节点。

线性方程组解耦

对于一般形式的无输入的状态空间方程，我们需要通过解耦将其简化为易于分析的形式，其思路是利用特征值和特征向量将矩阵转化为对角矩阵。

线性代数的知识这里只简单引入，给定一个方阵$\mathbf{A}$，如果向量$\mathbf{v}$经$\mathbf{A}$线性变换后，得到的新的向量与原向量$\mathbf{v}$共线，则向量$\mathbf{v}$为矩阵$\mathbf{A}$的特征向量，即

$$\mathbf{Av}=\lambda \mathbf{v}$$

其中$\lambda \ne 0$为矩阵$\mathbf{A}$的特征值。

求解特征值与特征向量的步骤如下

$$\begin{array}{c}\mathbf{Av}-\lambda \mathbf{v}=0\\ \Rightarrow (\mathbf{A}-\lambda \mathbf{I})\mathbf{v}=0\\ \Rightarrow |\mathbf{A}-\lambda \mathbf{I}|=0\end{array}$$

将最终的行列式展开得到的方程称为矩阵$\mathbf{A}$的特征方程，可以得到其特征值。

现在对于一般形式的状态空间方程

$$\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\mathbf{Az}(t)$$

设$n\times n$矩阵$\mathbf{A}$的一系列特征向量为${\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n$，则定义过渡矩阵为

$$\mathbf{P}=[{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n]$$

其具有如下性质

$$\mathbf{AP}=\mathbf{PD}$$

其中$\mathbf{D}$是一个特征值位于对角线上的对角矩阵

$$\mathbf{D}=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]$$

下面定义一组新的状态变量$\bar{\mathbf{z}}(t)$，令

$$\mathbf{z}(t)=\mathbf{P}\bar{\mathbf{z}}(t)$$

将其代入状态空间方程得

$$\mathbf{P}\frac{\mathrm{d}\bar{\mathbf{z}}(t)}{\mathrm{d}t}=\mathbf{AP}\bar{\mathbf{z}}(t)$$

等式两边同时左乘${\mathbf{P}}^{-1}$得

$$\begin{array}{c}{\mathbf{P}}^{-1}\mathbf{P}\frac{\mathrm{d}\bar{\mathbf{z}}(t)}{\mathrm{d}t}={\mathbf{P}}^{-1}\mathbf{AP}\bar{\mathbf{z}}(t)\\ \Rightarrow \frac{\mathrm{d}\bar{\mathbf{z}}(t)}{\mathrm{d}t}=\mathbf{D}\bar{\mathbf{z}}(t)\end{array}$$

由于$\mathbf{D}$是对角矩阵，所以新的状态变量${\bar{z}}_1(t),{\bar{z}}_2(t),\cdots ,{\bar{z}}_n(t)$的变化量只和自身相关，达到了解耦的效果。根据微分方程的求解公式可得

$${\bar{z}}_i(t)=C_i{e}^{{\lambda }_{i}t}(i=1,2,\cdots ,n)$$

再将新的状态变量代回$\mathbf{z}(t)=\mathbf{P}\bar{\mathbf{z}}(t)$即可求出原状态变量。

一般形式

在一般形式下，假设我们已经求解出解耦后新状态变量$\bar{\mathbf{z}}(t)$的相轨迹，以下面这个式子为例

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[\begin{array}{c}{\bar{z}}_1(t)\\ {\bar{z}}_2(t)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}{\bar{z}}_1(t)\\ {\bar{z}}_2(t)\end{array}\right]$$

现在要还原原状态变量$\mathbf{z}(t)$的相轨迹，例如已知$\mathbf{z}(t)$与$\bar{\mathbf{z}}(t)$的关系为

$$\mathbf{z}(t)=\mathbf{P}\bar{\mathbf{z}}(t)=\left[\begin{array}{cc}3& 1\\ 1& 3\end{array}\right]\left[\begin{array}{c}{\bar{z}}_1(t)\\ {\bar{z}}_2(t)\end{array}\right]={\bar{z}}_1(t)\left[\begin{array}{c}3\\ 1\end{array}\right]+{\bar{z}}_2(t)\left[\begin{array}{c}1\\ 3\end{array}\right]$$

由此看出$\mathbf{z}(t)$是$\bar{\mathbf{z}}(t)$的线性变换，因而$\bar{\mathbf{z}}(t)$的相轨迹也经该线性变换映射到$\mathbf{z}(t)$上

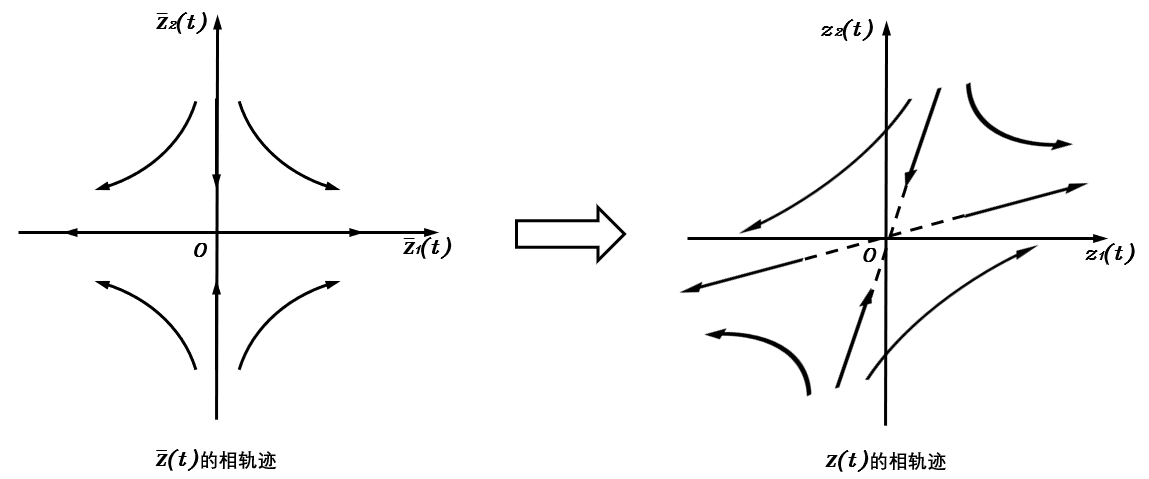
线性变换不会改变平衡点的性质，此平衡点仍然是一个鞍点。

对于特征值和特征向量存在复数的情况，线性变换将不再适用，此时需要从解入手分析。以下面这个系统为例简单介绍其分析思路

$$\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\left[\begin{array}{cc}0& 4\\ -1& 0\end{array}\right]\mathbf{z}(t)$$

其状态矩阵的特征值和特征向量为

$$\{\begin{array}{c}{\lambda }_1=2\mathrm{j}\\ {\lambda }_2=-2\mathrm{j}\end{array}\{\begin{array}{c}{\mathbf{v}}_1=\left[\begin{array}{c}2\\ \mathrm{j}\end{array}\right]\\ {\mathbf{v}}_2=\left[\begin{array}{c}2\\ -\mathrm{j}\end{array}\right]\end{array}$$

利用解耦方法可以最终求得（中途代入欧拉公式$e^{\mathrm{j}t}=\cos t+\mathrm{j}\sin t$）

$$\mathbf{z}(t)=\left[\begin{array}{c}2(C_1+C_2)\cos 2t+2(C_1-C_2)\mathrm{j}\sin 2t\\ (C_1-C_2)\mathrm{j}\cos 2t-(C_1+C_2)\sin 2t\end{array}\right]$$

整理后可以发现$z_1(t),z_2(t)$满足下列方程

$${\left(\frac{z_1(t)}{4\sqrt{C_1{C}_2}}\right)}^2+{\left(\frac{z_2(t)}{2\sqrt{C_1{C}_2}}\right)}^2=1$$

这是一个以原点为中心的椭圆方程，说明$z_1(t),z_2(t)$在相平面中沿着椭圆的轨迹运行

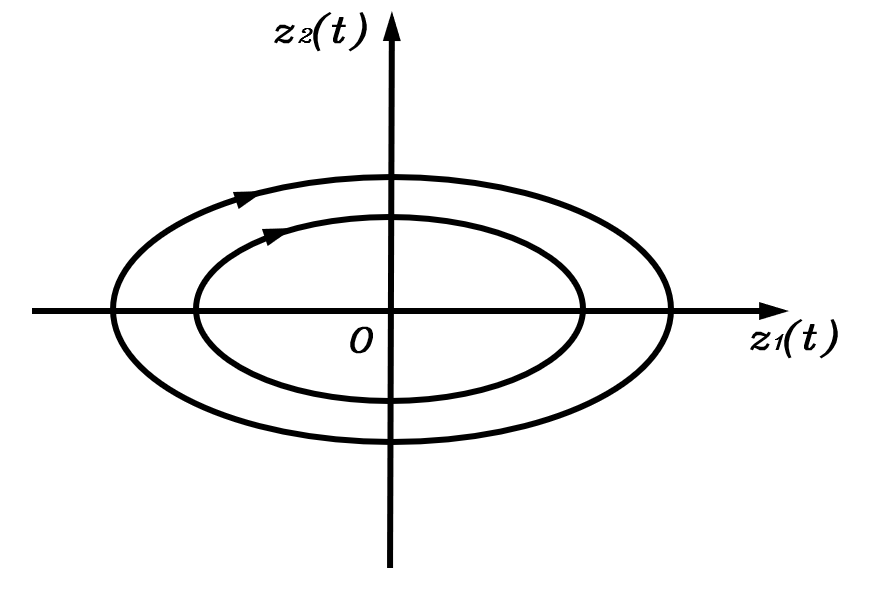
相轨迹的运动方向可以通过在坐标轴上选取一个点分析其各状态变量的导数正负来判断。其中位于椭圆中心的平衡点称为中心点，相轨迹围绕该点做椭圆运动。