【分层强化学习】#6 HIRO：离轨策略经验校正

在此前介绍的深度分层强化学习算法中，Option-Critic是同轨策略（On-Policy）算法，它将当前策略与环境交互收集的样本立即用于更新策略，即用即弃，更新准确但数据利用率低；h-DQN和FeUdal Networks是离轨策略（Off-Policy）算法，它们存储整个学习过程中产生的经验，并随时利用其中的小批量来更新策略，数据利用率高，但是会用旧策略的数据更新新策略，带来行为策略和目标策略不匹配的问题。然而h-DQN和FeUdal Networks并没有采用重要度采样方法来纠正这一偏差，因为高层策略的重要度采样极其困难：

• 高层目标的回报同时受制于高层策略和低层策略的影响；
• 低层策略的同时学习对于高层策略而言破坏了旧数据和新数据之间的相关性，这不符合重要度采样的基本假设；
• 高层策略的一次决策会覆盖多个时间步，这使得重要度采样中累乘的计算会带来巨大的方差，一个微小的概率差异可能会产生数值爆炸或消失。

HIRO

HIRO（Hierarchical Reinforcement learning with Off-policy correction，带离策略校正的分层强化学习）专注于解决低层策略持续更新为高层策略训练带来的偏差问题，其核心在于利用离策略校正机制，让高层策略能够更有效地复用低层策略的经验，为重要度采样提供了一种实用的替代方案。

策略架构与低层策略训练

HIRO采用双层策略架构，由低层策略${\mu }^{lo}$和高层策略${\mu }^{hi}$组成。在每个时间步$t$：

• 高层策略${\mu }^{hi}$观测环境状态$s_t$，并且每$c$个时间步采样目标$g_t\sim {\mu }^{hi}$，其他时间步的目标则来自一个目标转换函数$g_t=h(s_{t-1},g_{t-1},s_t)$；
• 低层策略${\mu }^{lo}$观测状态$s_t$和目标$g_t$，并采样动作$a_t\sim {\mu }^{lo}(s_t,g_t)$；
• 环境从奖励函数$R(s_t,a_t)$中采样奖励$R_t$，并转移到从状态转移函数$f(s_t,a_t)$采样的新状态$s_{t+1}$。

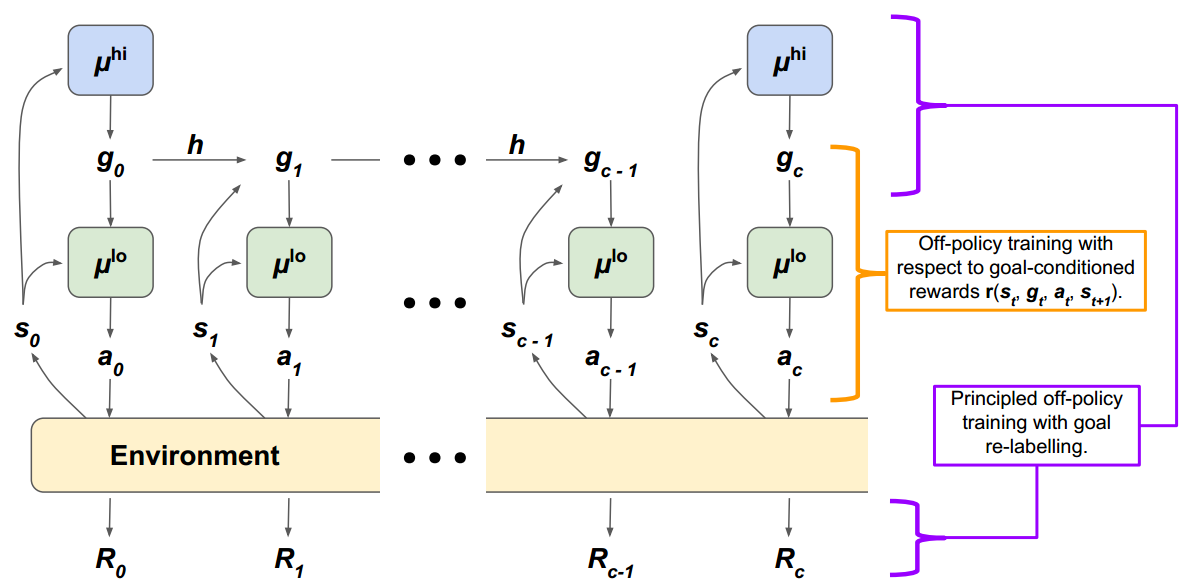
与FuN类似，HIRO的目标$g_t$被定义为期望的状态变化量。即在高层策略决策点，对于当前状态$s_t$和高层策略产生的目标$g_t$，高层控制器希望低层控制器采取动作，使$c$步之后的状态$s_{t+c}$尽可能接近$s_t+g_t$。而在此期间，为了保证目标指向的状态固定，目标转换函数的定义为

$$g_{t+1}=h(s_t,g_t,s_{t+1})=s_t+g_t-s_{t+1}$$

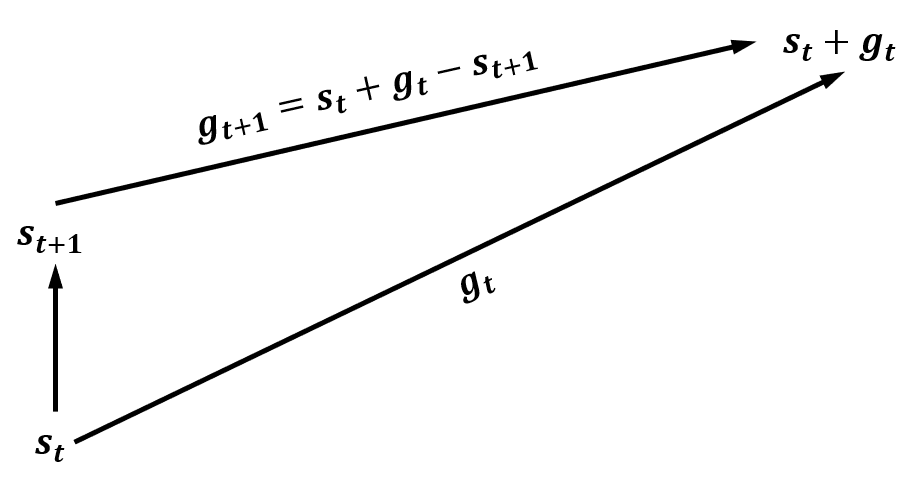
相应地，低层策略的内部奖励被设置为负的当前状态与目标状态之间的距离

$$r(s_t,g_t,a_t,s_{t+1})=-\Vert s_t+g_t-s_{t+1}{\Vert }_2$$

HIRO仅使用内部奖励，采用与DDPG或TD3相同的确定性策略训练范式训练低层策略。低层策略的Critic网络使用如下TD误差作为梯度更新参数（以DDPG为例，$Q_{\theta }^{lo}{}^{\prime }$为目标网络）

$$r(s_t,g_t,a_t,s_{t+1})+\gamma Q_{\theta }^{lo}{}^{\prime }(s_{t+1},g_{t+1},{\mu }_{\varphi }^{lo}(s_{t+1},g_{t+1}))-Q_{\theta }^{lo}(s_t,g_t,a_t)$$

Actor网络使用确定性策略梯度

$${\nabla }_{\theta }J({\mu }_{\varphi }^{lo})={\mathbb{E}}_{s\sim {\rho }^{lo}}[{\nabla }_{\theta }{\mu }_{\varphi }^{lo}(s,g){\nabla }_a{Q}^{lo}(s,g,a){|}_{a={\mu }_{\varphi }^{lo}(s,g)}]$$

离策略校正与高层策略训练

HIRO同样使用基于DDPG或TD3的方法训练高层策略，其Critic网络的TD误差为（以DDPG为例）

$$R_{t:t+c-1}+\gamma \underset{g}{\max }{Q}_{\varphi }^{hi}{}^{\prime }(s_{t+c},g)-Q_{\varphi }^{hi}(s_t,g_t)$$

但是为了解决重要度采样的问题，HIRO进一步对其所使用的经验样本进行了处理。在HIRO中，用于训练高层策略的原始经验是一个五元组$(s_{t:t+c-1},g_{t:t+c-1},a_{t:t+c-1},R_{t:t+c-1},s_{t+c})$，其中$x_{t:t+c-1}$表示从$t$到$t+c-1$的序列$x_t,\cdots ,x_{t+c-1}$。

HIRO进行异策略校正的核心思路是，为了在新低层策略的基础上训练高层策略，我们需要修正旧经验中的目标$g_t$为${\tilde{g}}_t$，使得新低层策略根据修正目标${\tilde{g}}_t$，能够复刻旧低层策略根据原始目标$g_t$产生的动作序列$a_{t:t+c-1}$。换言之，我们要将经验中的$g_t$替换为${\tilde{g}}_t$，以最大化概率${\mu }^{lo}(a_{t:t+c-1}|s_{t:t+c-1},{\tilde{g}}_{t:t+c-1})$，这一操作即为离策略校正。后续时间步的目标采用目标转换函数${\tilde{g}}_{t+1}=h(s_t,{\tilde{g}}_t,s_{t+1})$递推得出。修正后的经验变为$(s_t,{\tilde{g}}_t,R_{t:t+c-1},s_{t+c})$，无需存储原始动作序列、中间状态和中间目标。

但是HIRO采用了确定性策略作为低层策略，为此HIRO采用以${\mu }^{lo}(s,g)$为中心的高斯分布随机性策略来近似${\mu }^{lo}(s,g)$，则关于对数概率$\log {\mu }^{lo}(a_{t:t+c-1}|s_{t:t+c-1},{\tilde{g}}_{t:t+c-1})$有

$$\log {\mu }^{lo}(a_{t:t+c-1}|s_{t:t+c-1},{\tilde{g}}_{t:t+c-1})\propto -\frac{1}{2}\sum _{i=t}^{t+c-1}\Vert a_i-{\mu }^{lo}(s_i,{\tilde{g}}_i){\Vert }_2^2+\mathrm{const}$$

即最大化对数概率$\log {\mu }^{lo}(a_{t:t+c-1}|s_{t:t+c-1},{\tilde{g}}_{t:t+c-1})$等价于最小化${\sum }_{i=t}^{t+c-1}\Vert a_i-{\mu }^{lo}(s_i,{\tilde{g}}_i){\Vert }_2^2$。我们可以理解为，针对确定性策略，HIRO将动作概率最大化问题转化为了动作输出的均方误差最小化问题。

不过要精确求解这一最小化问题也很复杂，HIRO选择通过近似采样将其工程化。HIRO从10个候选目标中搜索最小化均方误差的局部解，其中有两个确定性候选目标$g_t$和$s_{t+c}-s_t$，剩余的8个随机候选目标将从以$s_{t+c}-s_t$为均值的高斯分布中采样。HIRO基于对问题的认知，将已有的$g_t$和$s_{t+c}-s_t$作为先验知识，并假设最可能的修正目标大概率位于实际发生的状态变化附近。

通过重要度采样我们可以进一步认识动作重标记的理论基础。在原始的重要度采样方法下，对于产生经验的对应低层行为策略${\mu }_{\beta }^{lo}(a_i|s_i,g_i)$和从经验中学习的对应低层目标策略${\mu }^{lo}(a_i|s_i,g_i)$，我们需要将以行为策略分布的经验通过重要度采样比$w_t$转换为以目标策略分布

$$\begin{array}{rl}L(\theta )& =\mathbb{E}[(Q_{\theta }^{hi}(s_t,g_t)-y_t{)}^2]\\ y_t& =\prod _{i=t}^{t+c-1}({\mu }^{lo}(a_i|s_i,g_i)p(s_{i+1}|s_i,a_i))\left[R_{t:t+c-1}+\gamma \underset{g}{\max }{Q}^{hi}(s_{t+c},g)\right]\\ y_t& =\prod _{i=t}^{t+c-1}({\mu }_{\beta }^{lo}(a_i|s_i,g_i)p(s_{i+1}|s_i,a_i))\left[w_t\cdot \left(R_{t:t+c-1}+\gamma \underset{g}{\max }{Q}^{hi}(s_{t+c},g)\right)\right]\\ w_t& =\prod _{i=t}^{t+c-1}\frac{{\mu }^{lo}(a_i|s_i,g_i)}{{\mu }_{\beta }^{lo}(a_i|s_i,g_i)}\end{array}$$

而行为重标记相当于修正目标策略分布中的$g_i$为${\tilde{g}}_i$，使得重要度采样比近似为$1$

$$w_t=\prod _{i=t}^{t+c-1}\frac{{\mu }^{lo}(a_i|s_i,{\tilde{g}}_i)}{{\mu }_{\beta }^{lo}(a_i|s_i,g_i)}\approx 1$$

相当于找到${\tilde{g}}_i$以最小化$w_t$与$1$的误差

$${\tilde{g}}_t=\arg \underset{g_t}{\min }\left(1-\prod _{i=t}^{t+c-1}\frac{{\mu }^{lo}(a_i|s_i,g_i)}{{\mu }_{\beta }^{lo}(a_i|s_i,g_i)}\right)$$

对右侧取对数

$${\tilde{g}}_t=\arg \underset{g_t}{\min }\left(\sum _{i=t}^{t+c-1}(\log {\mu }^{lo}(a_i|s_i,g_i)-\log {\mu }_{\beta }^{lo}(a_i|s_i,g_i))\right)$$

该优化目标与行为重标记相符。由于不能保证存在${\tilde{g}}_t$使得损失函数为零，因此该估计是有偏的，但在工程中可以接受，且换来了训练所需的稳定性和低方差。

算法流程

现在我们可以得出HIRO的算法伪代码如下：

（原论文没有给出伪代码，博主自行给出，仅供参考。DDPG和TD3相关细节省略）

1. 初始化：
   1. 高层策略${\mu }_{\varphi }^{hi}$及其Critic网络$Q_{\theta }^{hi}$；
   2. 低层策略${\mu }_{\varphi }^{lo}$及其Critic网络$Q_{\theta }^{lo}$；
   3. 目标网络${\mu }_{\varphi }^{hi}{}^{\prime }\leftarrow {\mu }_{\varphi }^{hi}$，$Q_{\theta }^{hi}{}^{\prime }\leftarrow Q_{\theta }^{hi}$，${\mu }_{\varphi }^{lo}{}^{\prime }\leftarrow {\mu }_{\varphi }^{lo}$，$Q_{\theta }^{lo}{}^{\prime }\leftarrow Q_{\theta }^{lo}$；
   4. 超参数：高层决策间隔$c$，经验回放缓冲区${\mathcal{D}}_{hi},{\mathcal{D}}_{lo}$，软更新速率$\tau$。
2. 对每一幕循环：
   1. 初始化状态$s_0$；
   2. 高层策略采样初始目标$g_0\sim {\mu }_{\varphi }^{hi}(s_0)$；
   3. 对每个时间步$t$循环：
      1. 低层策略执行动作$a_t\sim {\mu }_{\varphi }^{lo}(s_t,g_t)+\mathcal{N}(0,{\sigma }_{lo})$（高斯噪声探索）；
      2. 观测到奖励$R_t$和后继状态$s_{t+1}$；
      3. 计算内在奖励$r_t$；
      4. 计算后继目标$g_{t+1}$；
      5. 将低层经验$(s_t,g_t,a_t,r_t,s_{t+1},g_{t+1})$存入缓存区${\mathcal{D}}_{lo}$；
      6. 从${\mathcal{D}}_{lo}$采样一个批次经验，根据DDPG或TD3的更新规则更新${\mu }_{\varphi }^{lo}$和$Q_{\theta }^{lo}$；
      7. 软更新目标网络${\mu }_{\varphi }^{lo}{}^{\prime }$和$Q_{\theta }^{lo}{}^{\prime }$；
      8. 如果$t+1\%c=0$：
         1. 计算当前段总奖励$R_{t-c+1:t}$；
         2. 将高层经验$(s_{t-c+1},g_{t-c+1},a_{t-c+1:t},R_{t-c+1:t},s_t)$存入缓存区${\mathcal{D}}_{hi}$；
         3. 高层策略采样目标$g_{t+1}\sim {\mu }_{\varphi }^{hi}(s_{t+1})$。
      9. 从${\mathcal{D}}_{hi}$采样一个批次经验，修正为$(s_{t-c+1},{\tilde{g}}_{t-c+1},R_{t-c:t},s_t)$（原始经验保留，修正经验更新后丢弃）；
      10. 使用修正后的经验批次，根据DDPG或TD3的更新规则更新${\mu }_{\varphi }^{hi}$和$Q_{\theta }^{hi}$；
      11. 软更新目标网络${\mu }_{\varphi }^{hi}{}^{\prime }$和$Q_{\theta }^{hi}{}^{\prime }$。