Educational Codeforces Round 86 (Rated for Div. 2) C. Yet Another Counting Problem 数论

题目传送


题意:
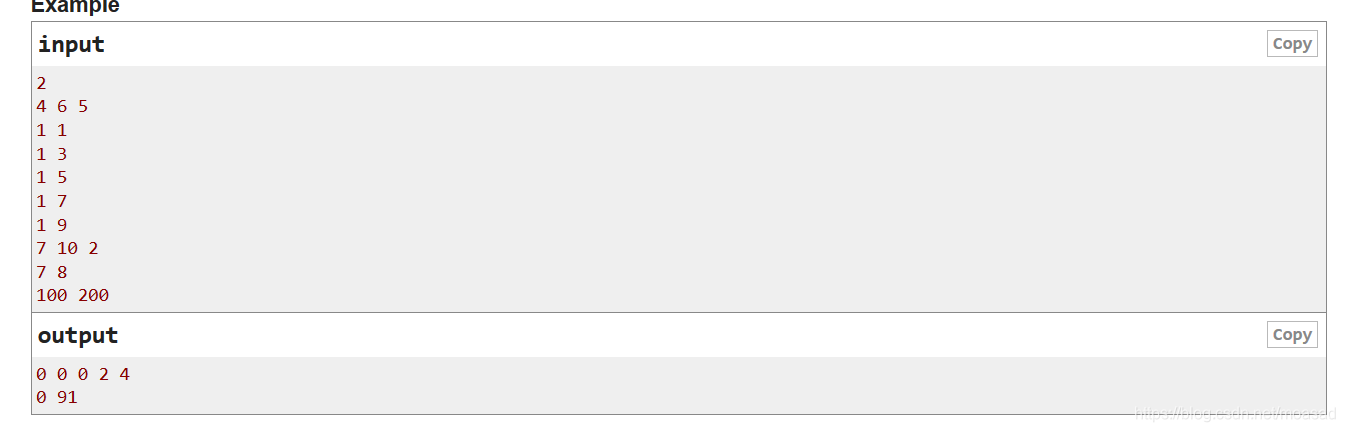
题意到是很简单，就是给你a，b。问在给定的 l 到 r 区间内，有多少个数使得 num % a % b != num % b % a。

思路:
这个，我是打表发现规律的，至于证明，打表出来后，自己想想就觉得有道理。
首先，打表出来发现，num % a % b == num % b % a的数呈周期出现，且周期为max(a,b)，每个周期的开始的第一个元素为a，b的最小公倍数的倍数，且小于max(a,b)的数也不行。
数论的题，就是思维，考数学了，自己在比赛的时候右边界出了问题，我直接把这个与0比较然后加上，但是当x小于最小公倍数的时候，就不行，没有solve函数里面的if特判，导致自己没有a掉这个题。。。。。

AC代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
ll a,b,q,Lcm;
ll solve(ll x)
{
    ll sum = x - x/Lcm*max(a,b) - min(max(a,b)-1,x);
    if(x/Lcm*Lcm+max(a,b) > x && x/Lcm != 0) sum +=  max((ll)0,x/Lcm*Lcm+max(a,b)-1-x);
    return sum;
}
int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    ll t;
    cin >> t;
    while(t--)
    {
        cin >> a >> b >> q;
        Lcm = a*b/__gcd(a,b);
        while(q--)
        {
            ll l,r;
            cin >> l >> r;
            cout << solve(r)-solve(l-1) << endl;
        }
    }
}