DP——最长公共子序列及最短编辑距离_最长公共子序列 dp-优快云博客

本文链接：https://blog.youkuaiyun.com/mo8181/article/details/125571147

本文详细介绍了如何使用动态规划解决最长公共子序列和最短编辑距离两个经典问题，并提供了完整的C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最长公共子序列

最长公共子序列问题我们用 $i$ 表示字符串 $A$ 的前 $i$ 个字符， $j$ 表示字符串 $B$ 的前 $j$ 个字符， $f [i, j]$ 表示前 $i$ 个字符和前 $j$ 个字符中的公共子序列的最大长度，对于以 $a [i], b [j]$ 结尾的子序列，一共有四种情况，分别为包含或者不包含 $a [i], b [j]$ ,那么 $f [i, j]$ 可以由 $f [] i - 1, j - 1], f [i - 1, j], f [i, j - 1], f [i - 1, j - 1] + 1$ 四种情况求最大值可得到，其中 $f [i - 1, j - 1]$ 的情况包含在了 $f [i - 1, j], f [i, j - 1]$ 两种情况中，注意子序列中含 $a [i]$ ,不含 $b [j]$ 的情况包含在了 $f [i, j - 1]$ 中，但两者并不相等。因为是求最大值，所以可以有重复的情况，只要求得所有情况的最大值即可。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= m; i ++) cin >> b[i];
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
        {
            f[i][j] = max(f[i][j - 1], f[i - 1][j]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
    }
    
    cout << f[n][m] << endl;
    return 0;
}

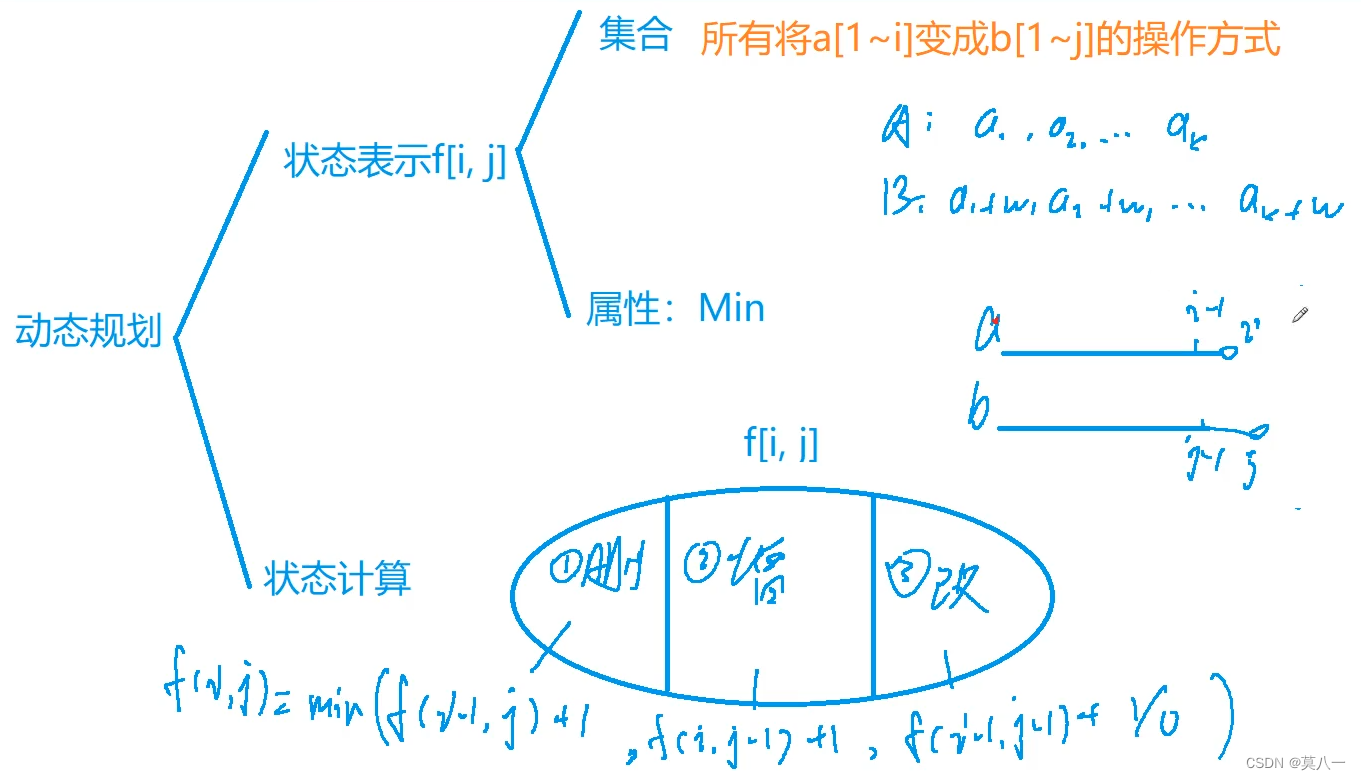
最短编辑距离

最短编辑距离类似于公共子序列问题，我们对于将 $a [1 i]$ 变成 $b [1 j]$ 一共有三种方式，删除当前 $a [i]$ 使得其相等，等价于 $f [i - 1, j] + 1$ ;增加一个数使得其相等，则增加的数一定的 $b [j]$ ，等价于求 $f [i, j - 1] + 1$ ,此时注意，增加操作是使得 $a [1 i]$ 与 $b [1 j]$ 相等；修改操作需要判断当前的 $a [i]$ 与 $b [j]$ 是不是相等，若相等则不用修改，不相等则需要修改。
在这里插入图片描述

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    cin >> m;
    for(int j = 1; j <= m; j ++) cin >> b[j];
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            f[i][j] = 1e9;
            
    for(int i = 1; i <= n; i ++) f[i][0] = i;
    for(int i = 1; i <= m; i ++) f[0][i] = i;
    
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j <= m; j ++)
        {
            f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
            if(a[i] != b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
            else f[i][j] = f[i - 1][j - 1];
        }
    }
    
    int s = f[n][m];
    
    cout << s << endl;
    return 0;
}