机器学习算法梳理—线性回归

介绍

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。^[1]

一、相关概念

1.损失函数

损失函数（Loss function）是用来估量你模型的预测值 f(x) 与真实值 Y 的差异程度，它是一个非负实值函数，通常用 L(Y,f(x)) 来表示（即变量为真实值与预测值的函数）。损失函数越小，模型的鲁棒性就越好。^[2]
一句话概括就是：损失函数计算的是一个样本的误差。

2.代价函数

代价函数和损失函数是同一个东西，是整个训练集上所有样本误差的平均。^[3]

3.目标函数

目标函数是一个与损失函数、代价函数相关的函数，但是概念更广。对于目标函数来说在有约束条件下的最小化就是损失函数（loss function）。
一句话概括就是：代价函数（损失函数） + 正则化项。

目标函数、损失函数、代价函数三者的区别见下面第9条！

4.正则化

正则化与模型的复杂度有关，一般模型越复杂，正则化值就越大。正则化的一般形式如下：

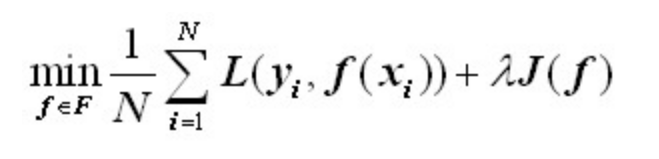
其中，第一项是经验风险，第二项是正则化项，正则化项可以取不同的形式，例如，正则化项可以是模型参数向量的范数。回归问题中，损失函数是平方损失，正则化项可以是参数向量（w）的L2范数：

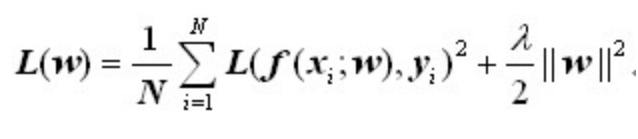
根据奥卡姆剃刀原理：在所有可能的模型中，能够更好的解释已知数据并且十分简单才是最好的模型，也就是应该选择的模型。

5.交叉验证

一般情况，当数据比较充足时，采用可以将数据集分为训练集，验证集，测试集。训练集训练出多个模型后，通过验证集选择最小预测误差的模型。
当数据不充足时，采用交叉验证方法，它的基本思想是重复利用数据进行切分，将切分后的数据集组合为训练集和测试集，在此基础上反复进行训练测试。
例如将数据集分为70%为训练集，30%为测试集，通过训练集中训练得到不同模型，然后在测试集中测试各个模型误差，选出误差最小的模型。

6.过拟合

所谓过拟合（overfitting），指的是模型在训练集上表现的很好，但是在交叉验证集合测试集上表现一般，也就是说模型对未知样本的预测表现一般。
过拟合采用了很复杂的模型。最后导致曲线波动很大，最后最可能出现的结果就是模型对于未知样本的预测效果很差。
防止过拟合方法：
（1）迭代次数截断的方法（early stopping）
（2）数据集扩增（Data augmentation）
（3）正则化（Regularization）

7.泛化能力

泛化能力就是模型对未知数据的预测能力。在实际当中，我们通常通过测试误差来评价学习方法的泛化能力。
泛化误差的定义：^[3]

大家很快就能发现，这是损失函数的期望。如果一种方法学习的模型比另外一种方法学习的模型拥有更小的泛化误差，那么这种方法就更有效。

8.模型评估

有了测试集之后，使用什么指标来度量模型的好坏程度呢？不同的任务需求，会使用不同的性能度量指标，在回归和分类任务中，性能度量的指标也完全不一样。\

（1）回归问题

回归问题的标记yi一般都是实值，不能通过是否相等进行评估。一般是通过衡量预测值f(xi)和真实值yi之间的距离。
线性回归常用的评价指标有均方误差等。

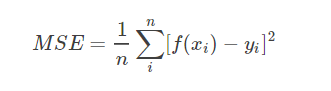
（2）分类问题

分类问题中评价指标有6种方法：^[4]

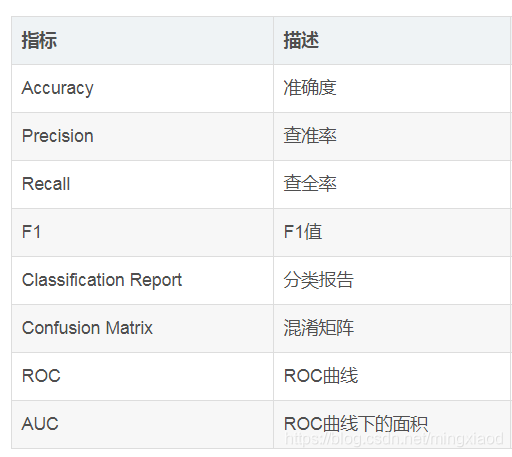
9.目标函数、损失函数、代价函数的区别：

举例说明：^[5]

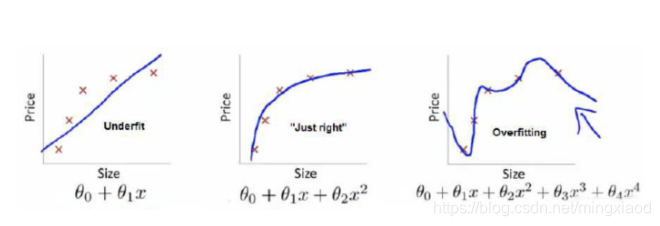
上面三个图的函数依次为 f1(x) , f2(x) , f3(x) 。我们是想用这三个函数分别来拟合Price，Price的真实值记为 Y 。
我们给定 x ，这三个函数都会输出一个 f(X) ,这个输出的 f(X) 与真实值 Y 可能是相同的，也可能是不同的，为了表示我们拟合的好坏，我们就用一个函数来度量拟合的程度，比如：

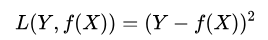
这个函数就称为损失函数(loss function)，或者叫代价函数(cost function)。损失函数越小，就代表模型拟合的越好。
那是不是我们的目标就只是让loss function越小越好呢？还不是。
这个时候还有一个概念叫风险函数(risk function)。风险函数是损失函数的期望，由于我们输入输出的（X,Y）遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集， f（x）关于训练集的平均损失称作经验风险(empirical risk)，即：

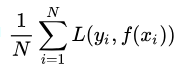
所以我们的目标就是最小化 上述函数，称为经验风险最小化。
此时再看上面三个函数曲线，很明显 f3(x) 把所有数据都考虑进去，经验风险最小！ 但是由于 f3(x) 过拟合，明显不是我们想要的结果。由于它的函数太复杂，因此需要加入函数复杂度来进行约束！此时正好有一个函数J（f），用来度量模型的复杂度，在机器学习中叫正则化(regularization)，正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值越大。常用的有 L1 , L2 范数。把这个过程叫结构风险最小化。
所以最终我们的优化函数变为：

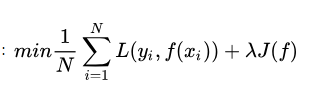
即最优化经验风险和结构风险，而这个函数就被称为目标函数。
综上：
最左面的 f1(x) 结构风险最小（模型结构最简单），但是经验风险最大（对历史数据拟合的最差）；最右面的 f3(x) 经验风险最小（对历史数据拟合的最好），但是结构风险最大（模型结构最复杂）；而 f2(x) 达到了二者的良好平衡，最适合用来预测未知数据集。

二、线性回归原理

（1）线性回归概念：

线性回归是指在假设特征满足线性关系，是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合（自变量都是一次方）。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。

（2）线性回归模型：

在样本集D中有n个样本，即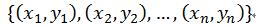。其中每个样本X有m个属性描述， X = (X1;X2;…;Xm)，其中Xi表示的是第i个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即：

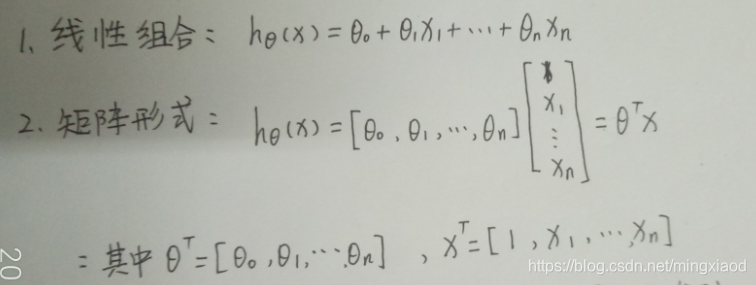
三、损失函数推导

我们把训练数据代入上面的设定模型后，可以通过模型预测一个样本最终值，但预测值与真实值之间是有误差ε：

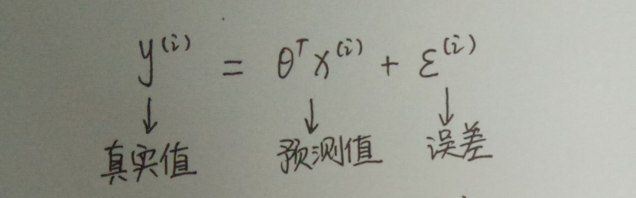
再假设训练样本的数据量很大的时候,根据中心极限定律可以得到 ε⁽ⁱ⁾ 满足 （u ,δ²）高斯分布的；由于方程有截距项 ，故使用可以 u =0; 故满足（0，δ²）的高斯分布，即：

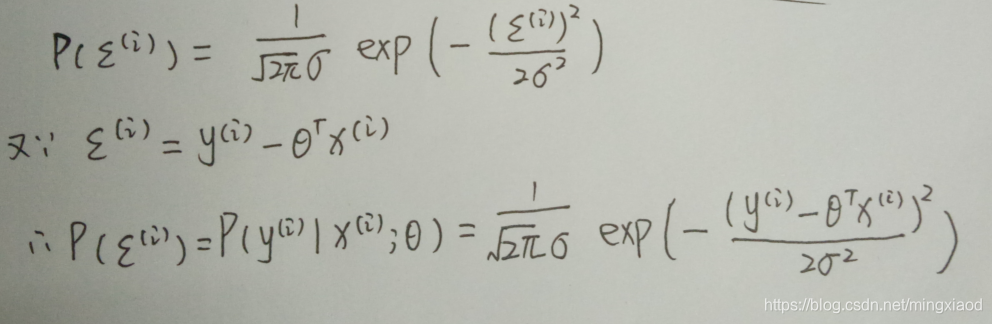
如上面可知，对于每一个样本 x ,代入到 p (y |x ;θ) 都会得到一个y 的概率；又因为设定样本是独立同分布的；对其求最大似然函数并化简：

以上就得到了回归的损失函数最小二乘法的公式。
总结：
根据大数定律和中心极限定律假定样本无穷大的时候，其真实值和预测值的误差ε 的加和服从u=0,方差=δ²的高斯分布且独立同分布，然后把ε =y-θx 代入公式，就可以化简得到线性回归的损失函数。

四、损失函数求解方法

对损失函数进行优化也就是求出θ，使的损失函数最小化。

（1）矩阵法（需要满足可逆条件）

以上就是按矩阵方法优化损失函数，但上面方法有一定的局限性，就是要可逆。

（1）梯度下降法

梯度下降法总体流程就如下图所示，就是求出每个变量θ的梯度；然后顺着梯度方向按一定的步长a,进行变量更新，最后将会收敛到局部最优点，使得优化函数局部最优。

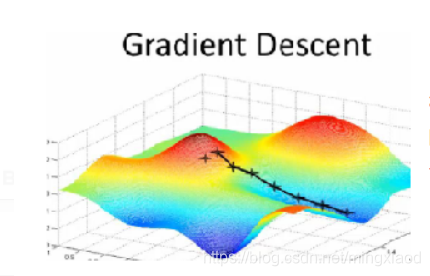
求出每个变量θ的梯度公式推导如下：

五、逻辑回归

逻辑回归与线性回归类似，但它不属于回归分析家族（主要为二分类），而属于分类家族，差异主要在于变量不同，逻辑回归是无监督学习的一个重要算法，对某些数据与事物的归属（分到哪个类别）及可能性（分到某一类别的概率）进行评估。
线性回归的预测值是实值，而当考虑二分类问题时，需要输出{0,1}，因此我们需要一个函数把线性回归的预测值转化为{0,1}值，这个就是很神奇的sigmoid函数。

sigmoid函数图像：

此时，回归模型变为：

在线性回归里，我们定义的代价函数是所有模型的误差平方和。理论上，我们可以在逻辑回归里沿用，但是，当我们把逻辑回归方程带入得出的代价函数如图：

它有多个低点，这样我们难以找到最优解，所以我们重新定义了逻辑回归的代价函数：


合并上面两个式子，得：

当我们得到了代价函数，我们就可以进行梯度下降的算法来求得我们想要的theta值。
损失函数为：

这个就是逻辑回归的梯度下降算法，形式上线性回归的一样，但是两个之间的h(x)是不同的，所以这是两个完全不同的东西。

六、sklearn参数详解

使用sklearn时候，如下两行代码即可导入线性模块：

from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(x_train, y_train)

linear_model中的函数方法
1.fit(X,Y,sample_weight=None)
用于拟合函数，X是训练集特征值，Y为训练集真实值，sample_weight是每条测试数据的权重,三个参数类型都是矩阵型
2.predict(X)
用于预测函数，对测试集的特征值进行预测
3.score(X,Y,sample_weight=None)
评分函数，将返回一个小于1的数值。X是测试集得特征值，Y是测试集得真实值
4.LinearRegreession将方程分为两个部分存放，coef_存放回归系数，intercept_存放截距，查看可以获得该回归方程。

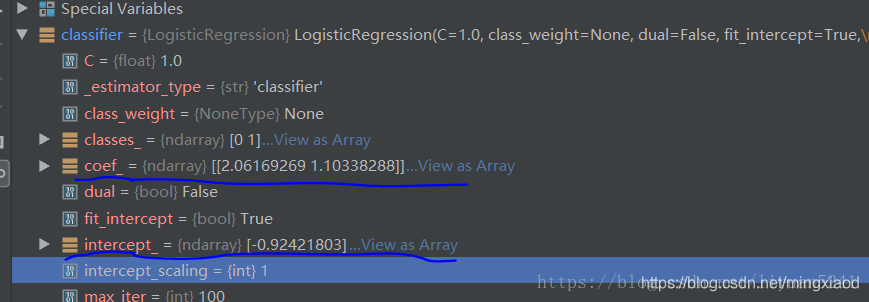
上图中的coef_变量对应模型参数ω，intercept 对应参数b 。

参考文献：

[1] 线性回归_百度百科：https://baike.baidu.com/item/线性回归/8190345?fr=aladdin
[2] 机器学习中的损失函数:https://blog.youkuaiyun.com/u010976453/article/details/78488279
[3] 机器学习–泛化能力:https://blog.youkuaiyun.com/fisherming/article/details/79499168
[4] 分类模型评估:https://blog.youkuaiyun.com/howhigh/article/details/73928627
[5] 机器学习中的目标函数、损失函数、代价函数有什么区别:https://www.zhihu.com/question/52398145