Double DQN

• 论文链接：https://arxiv.org/pdf/1509.06461.pdf
• 论文题目：Deep Reinforcement Learning with Double Q-learning

Double DQN

Abstract

Q-learning算法在特定情况下会存在过估计action values的情况。这种情况在实际应用中很普遍，而且会影响算法效果。之前并不知道原因以及能不能避免这种情况。本文我们会回答这两个问题。首先我们会在Atari领域中展示近期DQN算法出现的过估计问题，然后阐释Double Q-learning算法的思想。

Introduction

强化学习的目的是针对序列决策问题通过优化累积未来回报，来学会一个好的策略。Q-learning是其中一种流行的强化学习算法，但是已知有时候会学习到不现实的高动作价值，这是因为在估计动作价值的时候包含了一步最大值操作，这会使得agent倾向于过估计。
在之前的研究中，过估计的原因是不足够灵活的函数逼近以及噪声。本文，我们统一下这些观点，然后证明过估计会发生在动作价值不准确的时候，与函数逼近误差无关。当然，学习过程中不准确的价值预测是很常见的，这就说明过估计的发生可能比我们认为的还要普遍。
过估计的发生是否会对实际中的算法性能产生不良影响是一个开放问题。过分乐观的价值估计其实本质上并不是一个问题。如果所有的values都均匀的高于相对的参考actions，那么对于policy来说并不会有影响。甚至，有些时候乐观估计是有好处的：在面对不确定的时候，乐观主义是一种知名的探索方法。然而问题就是过估计是不均匀的，而且并不集中在我们想要更多去学习的states里。因此，它们会对policy性能产生坏影响。Thrun和Schwartz给出了具体的例子来证明这会导致最后渐进的收敛于次优。
我们证明Double Q-learning算法的思想可以泛化到任意的函数逼近的方法中，包括深度神经网络。我们使用该算法构建了一种新的算法，叫做Double DQN。该算法不仅得到更准确的价值预测，还在多个游戏中取得了更高的分数。

Background

这部分以及DQN部分我就不重复了，Dueling Network有类似的部分，就列一下会用到的方程
Q-learning的Q-target
$$Y_t^Q\equiv R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a;{\theta }_t)\text{\hspace{1em}(2)}$$
DQN的Q-target
$$Y_t^{DQN}\equiv R_{t+1}+\gamma \underset{a}{\max }Q(S_{t+1},a;{\theta }_t^{-})\text{\hspace{1em}(3)}$$

Double Q-learning

在标准Q-learning和DQN，也就是公式（2）和（3）中，使用了相同的value来选择和评估一个action。这就会使得大概率选择过估计的value，进而导致value的过乐观估计。为了防止这个问题，我们将评估和选择解耦合。这就是Double Q-learning（van Hasselt 2010）背后的核心思想。
在原始的Double Q-learning算法中，一共要学习两个价值函数（$\theta$和${\theta }^{\prime }$），每次学习都是将样本随机的用来更新其中一个价值函数。每一次更新，其中一套参数用来决定贪心策略（选择动作），另一个来确定value（评估动作）。为了作一个清晰的对比，我们可以先将Q-learning的选择和评估分解开，重新书写公式（2）：
$$Y_t^Q=R_{t+1}+\gamma Q(S_{t+1},\arg \underset{a}{\max }Q(S_{t+1},a;{\theta }_t);{\theta }_t)$$
对比Double Q-learning的target是：
$$Y_t^{DoubleQ}=R_{t+1}+\gamma Q(S_{t+1},\arg \underset{a}{\max }Q(S_{t+1},a;{\theta }_t);{\theta }_t^{\prime })\text{\hspace{1em}(4)}$$
注意到动作的选择仍然是使用在线权重${\theta }_t$。这意味着，就像在Q-learning里，我们仍然是根据当前value（${\theta }_t$）来估计贪心策略的value。然而，使用第二套参数（${\theta }_t^{\prime }$）来评价policy的value。通过变换${\theta }_t$和${\theta }_t^{\prime }$的角色，第二套参数也可以被更新。

Overoptimism due to estimation errors

Q-learning的过估计首先被Thrun和Schwartz发现的，他们发现如果一个action values含有均匀分布在区间$[-ϵ,ϵ]$内的随机误差，那么每个target就会被过估计$\gamma ϵ\frac{m-1}{m+1}$，这里$m$代表动作的数量。此外，他们还给出了一个具体的例子，这个例子里过估计会导致算法渐进地收敛到次优策略。后续 van Hasselt认为env里的噪声也会导致过估计，甚至在运用表格的时候，然后提出Double Q-learning是一个解决办法。
本节，我们会更加一般化地来说明任何的估计误差都会导致一个向上的偏置，不论这个误差是因为环境噪声，函数逼近，非平稳性还是什么源头。这非常重要，因为实际中任意方法在学习过程中都会引起一些不准确，因为最初我们对真值是一无所知的。
Thrun和Schwartz给出了在具体步骤中的过估计的上限，同时也可能可以推导出下限。
Theorem 1. 考虑一个state s，在这个state上，所有的真最优动作价值都等于某个$V_{\ast }(s)$，$Q_{\ast }(s,a)=V_{\ast }(s)$。定义Q_t是一个任意的价值估计，该估计整体上来说是无偏的，也就是${\sum }_a(Q_t(s,a)-V_{\ast }(s))=0$，但是它们并不都等于最优，也就是$\frac{1}{m}{\sum }_a(Q_t(s,a)-V_{\ast }(s){)}^2=C$，这里$C>0$，且$m\ge 2$是s里的actions的数量。在这样的条件下，${\max }_a{Q}_t(s,a)\ge V_{\ast }(s)+\sqrt{\frac{C}{m-1}}$。这个下限是严格的。在同样的条件下，Double Q-learning估计的绝对误差的下限是0。（证明见附录）
注意到我们并不需要假设不同actions的估计误差是独立的。这个定理说明了，即使价值估计的均值是正确的，但是任何的估计误差都会驱使估计往上远离真最优价值。
定理1中的下限会随着动作数量的增加而减小。这是在很人为地在考虑下限的时候，这需要获得非常具体的值才行。但是更典型的是，如图1，过估计会随着actions数量的增加而增加。Q-learning的过估计确实会随着动作数量而增加，而Double Q-Learning是无偏的。另一个例子，也是定理2：
Theorem 2. 如果所有的actions $Q_{\ast }(s,a)=V_{\ast }(s)$，并且估计误差$Q_t(s,a)-V_{\ast }(s)$是均匀随机分布于$[-1,1]$，那么过估计值为$\frac{m-1}{m+1}$（证明见附录）
（对于这里我自己的理解是，从公式的角度来说确实是随着动作数量越大下限是越低的，但是定理1中的这个C是人为设定的，在实际中，其实它应该不是一个定值，所以在实际应用中，动作数量越大，error是越大的。）

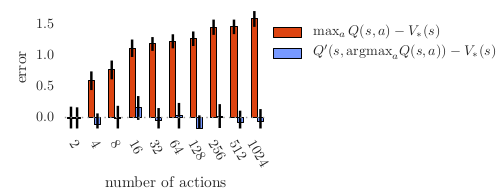
图1：橘色的柱状图显示的是single Q-learning更新时候的偏差，$Q(s,a)=V_{\ast }(s)+{ϵ}_a$，然后误差 { ϵ a } a = 1 m \{\epsilon_a\}^m_{a=1} {ϵa​}a=1m​是独立标准正态随机变量。蓝色柱状图代表$Q^{\prime }$，是独立同分布的。所有的bars都是100次重复的平均值。

我们现在来看函数逼近，考虑一个在每个state有10个离散动作的实数连续状态空间。为了简化，该例中的真最优动作价值仅取决于state，也就是每个state的所有actions都具有同样的真值。图2左列的图显示了真值（紫线），左上是$Q_{\ast }(s,a)=\sin (s)$，左中和左下是$Q_{\ast }(s,a)=2\exp (-s^2)$。左边的图显示了一个单一动作函数逼近（绿线），水平轴表示state，还显示了动作函数估计基于的采样点（绿点）。样本估计函数是一个d阶多项式，它是来拟合位于采样点的真值，上中行$d=6$，下行$d=9$。采样值完美的匹配了真值函数：没有噪声并且我们假设在采样点上我们有动作价值的gt。在上面两行我们发现函数拟合甚至无法保证采样点上的准确，这是因为函数近似不足够灵活（模型容量不够）。下行函数就足够灵活来拟合采样点，但是降低了未采样的state的准确率。注意到左图的左侧采样点与右侧有很大的间隙，这就会导致很大的估计误差。这是很典型的学习背景，在每个时间点，我们只有很有限的数据。
图2中间列展示了所有10个动作的动作价值函数估计（绿线），我们将每个state的最大值用黑虚线标记出来。尽管对于所有actions的真值函数都是一样的，函数拟合却不同，因为我们提供了不同的样本states集合。最大值通常是要高于gt的，左图紫色线。这在右图里也得到了印证，它展示了黑色曲线与紫色曲线的差异。橙色线几乎都是正值，也就展示了一个向上去的bias。右图同时也使用蓝线展示了Double Q-learning的估计，平均起来是非常接近于0的。这就说明了Double Q-learning确实能够成功的降低Q-learning的过估计。
图2的不同行展示了相同实验的不同变体。上和中的不同是真值函数，展示了过估计并不是因为特定的真值函数。中和下的区别是函数拟合的灵活性。左中图，因为函数不够灵活，估计在采样点上甚至都不对。左下图，函数更灵活但是对于没见过的state会造成更高的估计误差，进而造成过估计。灵活的参数函数逼近器经常会应用在RL中。
下行的图像展示了足够灵活的函数拟合能够cover所有的采样点也会导致很高的过估计。这就意味着过估计是普遍发生的。
那么价值估计会进一步恶化如果我们对已经过估计的值进行bootstrap off（再抽样，个人理解就是experience replay）。这是因为这会将过估计通过我们的估计进行传播。尽管均匀的过估计不会影响我们的最终策略，但是实际中的过估计误差是根据states以及actions的不同而不同的。结合bootstrap的过估计是有害的，它会将错误的相对信息传播，直接影响到学习策略的质量。
过估计不应该和不确定性优先（给states或者actions一个不确定的值作为探索红利）混淆。相反，这里讨论的过估计仅仅发生在更新之后，过估计是明显确定的优先。

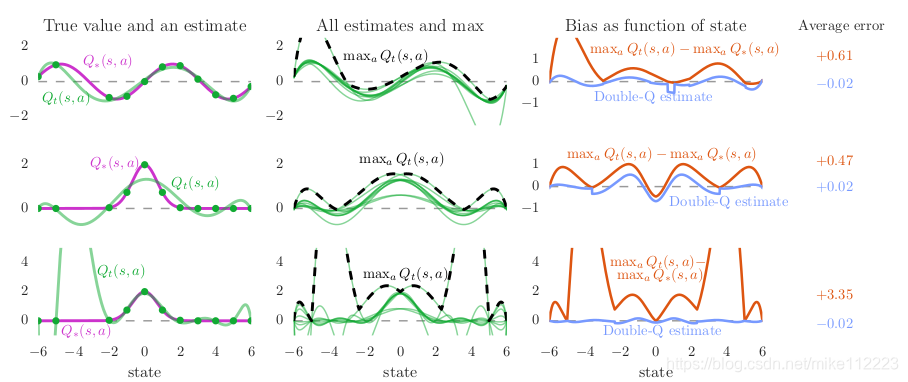
图2. 训练过程中的过估计。在每个state（x轴），有10个动作。左边那列展示了真值$V_{\ast }(s)$（紫色线）。所有的真值被定义为$Q_{\ast }(s,a)=V_{\ast }(s)$。绿色线展示的是对于一个action以state为参数的估计值$Q(s,a)$，在个别采样点上拟合了真值（绿点）。中间列的图展示的是所有的预测值（绿色），以及这些值的最大值（黑虚线）。最大值几乎比任何位置的真值都是高（左图紫色）。右列图中橘色显示的是差异。蓝线是对第二套样本用Double Q-learning对每个state做的预测。蓝线更接近与0，这就以为着小的bias。三行分别对应不同的真值函数（左图，紫）或者拟合函数的能力（左图，绿）

Double DQN

Double Q-learning的思想是通过将目标函数的最大值操作分解为动作选择和动作评估。尽管不是完全的解耦合，DQN框架中的目标网络提供了一个天然的对于第二个价值函数的候选，这就不需要我们再引入一个额外的网络了。因此，我们建议使用在线网络来评估贪心策略，然后使用目标网络来估计value。同时考虑Double Q-learning和DQN，我们得到算法Double DQN。它的更新和DQN一样，只不过替换目标$Y_t^{DQN}$：
$$Y_t^{DoubleDQN}\equiv R_{t+1}+\gamma Q(S_{t+1},\arg \underset{a}{\max }Q(S_{t+1},a;{\theta }_t),{\theta }_t^{-}).$$
相比于Double Q-learning的公式（4），第二个网络${\theta }_t^{-}$被target网络代替用来评估当前贪心策略。target网络跟DQN里一样，周期性地复制在线网络的参数。
该版本的Double DQN应该是改动最小的。

Appendix

定理1证明：

对于每个action $a$ 定义errors ${ϵ}_a=Q_t(s,a)-V_{\ast }(s)$。假设存在一个集合 { ϵ a } \{\epsilon_a\} {ϵa​}满足${\max }_a{ϵ}_a<\sqrt{\frac{C}{m-1}}$。定义 { ϵ i + } \{\epsilon^+_i\} {ϵi+​}为大小为$n$的正的$ϵ$集合， { ϵ j − } \{\epsilon^-_j\} {ϵj−​}为严格的负的$ϵ$集合，大小是$m-n$（ { ϵ } = { ϵ i + } ∪ { ϵ j − } \{\epsilon\}=\{\epsilon^+_i\} \cup \{\epsilon^-_j\} {ϵ}={ϵi+​}∪{ϵj−​}）。如果$n=m$，那么${\sum }_a{ϵ}_a=0⟹{ϵ}_a=0\forall a$，这与${\sum }_a{ϵ}_a^2=mC$矛盾。因此必然有$n\le m-1$。然后，${\sum }_{i=1}^n{ϵ}_i^{+}\le n{\max }_i{ϵ}_i^{+}<n\sqrt{\frac{C}{m-1}}$，因此（使用限制条件${\sum }_a{ϵ}_a=0$）我们同样有${\sum }_{j=1}^{m-n}|{ϵ}_j^{-}|<n\sqrt{\frac{C}{m-1}}$。这意味着${\max }_j|{ϵ}_j^{-}|<n\sqrt{\frac{C}{m-1}}$。通过Hölder’s inequality：
$$\begin{array}{rl}\sum _{j=1}^{m-n}({ϵ}_j^{-}{)}^2& \le \sum _{j=1}^{m-n}|{ϵ}_j^{-}|\cdot \underset{j}{\max }|{ϵ}_j^{-}|\\ & <n\sqrt{\frac{C}{m-1}}n\sqrt{\frac{C}{m-1}}.\end{array}$$
我们现在可以结合这些关系来计算一个所有${ϵ}_a$的平方和的上限：
$$\begin{array}{rl}\sum _{a=1}^m({ϵ}_a{)}^2& =\sum _{i=1}^n({ϵ}_i^{+}{)}^2+\sum _{j=1}^{m-n}({ϵ}_j^{-}{)}^2\\ & <n\frac{C}{m-1}+n\sqrt{\frac{C}{m-1}}n\sqrt{\frac{C}{m-1}}\\ & =C\frac{n(n+1)}{m-1}\\ & \le mC.\end{array}$$
这与我们的假设矛盾，因此通过反证法，我们有${\max }_a{ϵ}_a\ge \sqrt{\frac{C}{m-1}}$，对于所有背景的$ϵ$都满足这个限制。我们可以通过一个设定来检查这个下限的严格性，${ϵ}_a=\sqrt{\frac{C}{m-1}},a=1,...,m-1$，${ϵ}_m=-\sqrt{(m-1)C}$，同时也满足了${\sum }_a{ϵ}_a^2=mC,{\sum }_a{ϵ}_a=0$。
对于Double Q-learning来说，绝对误差的严格下限是0，$|Q_t^{\prime }(s,\arg {\max }_a{Q}_t(s,a))-V_{\ast }(s)|\ge 0$。这是因为我们可以有：
$$Q_t(s,a_1)=V_{\ast }(s)+\sqrt{C\frac{m-1}{m}},$$
还有
$$Q_t(s,a_i)=V_{\ast }(s)-\sqrt{C\frac{1}{m(m-1)}},\text{for }i>1.$$
定理所有的条件都符合。更进一步，如果我们有$Q_t^{\prime }(s,a_1)=V_{\ast }(s)$，那么误差就为0。剩下的$Q_t^{\prime }(s,a_i),i>1$就随意了。
（对于定理1，最后部分个人觉得有点问题，最后两个式子并没有满足定理1的所有条件，${\sum }_a{ϵ}_a=0$满足，但是${\sum }_a{ϵ}_a^2=mC$并不满足，最后的讲解稍微笼统了一点，个人觉得，其实就是将动作评估和选择解耦合，这样各自优化就没有限制，就没有下限了）

定理2证明：

定义${ϵ}_a=Q_t(s,a)-Q_{\ast }(s,a)$；这是一个位于$[-1,1]$的均匀随机变量。对于某个$x$，${\max }_a{Q}_t(s,a)\le x$的概率等于对于所有的$a$同时满足${ϵ}_a\le x$的概率。因为估计误差是独立的，我们可以推导：
$$\begin{array}{rl}P(\underset{a}{\max }{ϵ}_a\le x)& =P(X_1\le x\wedge X_2\le x\wedge ...\wedge X_m\le x)\\ & =\prod _{a=1}^{m}P({ϵ}_a\le x).\end{array}$$
函数$P({ϵ}_a\le x)$是${ϵ}_a$的累积分布函数（CDF），定义为：
$$P({ϵ}_a\le x)=\{\begin{array}{ll}0& \text{if }x\le -1\\ \frac{1+x}{2}& \text{if }x\in (-1,1)\\ 1& \text{if }x\ge 1\end{array}$$
我们有：
$$\begin{array}{rl}P(\underset{a}{\max }{ϵ}_a\le x)& =\prod _{a=1}^{m}P({ϵ}_a\le x)\\ & =\{\begin{array}{ll}0& \text{if }x\le -1\\ (\frac{1+x}{2}{)}^m& \text{if }x\in (-1,1)\\ 1& \text{if }x\ge 1\end{array}\end{array}$$
这就是随机变量${\max }_a{ϵ}_a$的CDF。它的期望可以写成积分形式：
$$\mathbb{E}[\underset{a}{\max }{ϵ}_a]={\int }_{-1}^{1}x{f}_{\max }(x)\text{d}x,$$
这里$f_{\max }$是这个变量的概率密度函数，定义为CDF的倒数：$f_{\max }(x)=\frac{\text{d}}{\text{d}x}P({\max }_a{ϵ}_a\le x)$，所以对于$x\in [-1,1]$我们有$f_{\max }(x)=\frac{m}{2}(\frac{1+x}{2}{)}^{m-1}$。
那么期望就是：
$$\begin{array}{rl}\mathbb{E}[\underset{a}{\max }{ϵ}_a]& ={\int }_{-1}^{1}x{f}_{\max }(x)\text{d}x\\ & =\left[\right(\frac{x+1}{2}{)}^m\frac{mx-1}{m+1}{]}_{-1}^1\\ & =\frac{m-1}{m+1}\end{array}$$