《Python数据分析基础教程：NumPy学习指南（第2版）》笔记7：第三章 常用函数3——最大值数组、卷积、指数、填充

本章将介绍NumPy的常用函数。具体来说，我们将以分析历史股价为例，介绍怎样从文件中载入数据，以及怎样使用NumPy的基本数学和统计分析函数。这里还将学习读写文件的方法，并尝试函数式编程和NumPy线性代数运算。

第三章 常用函数

3.17 真实波动幅度均值（ATR）

ATR（Average True Range，真实波动幅度均值）是一个用来衡量股价波动性的技术指标。ATR的计算并不是重点，只是作为演示几个NumPy函数的例子，包括maximum函数。

3.18 动手实践：计算真实波动幅度均值

按照如下步骤计算真实波动幅度均值。

• (1) ATR是基于N个交易日的最高价和最低价进行计算的，通常取最近20个交易日。

N = int(sys.argv[1])
h = h[-N:]
l = l[-N:]

• (2) 我们还需要知道前一个交易日的收盘价。

previousclose = c[-N -1: -1]

对于每一个交易日，计算以下各项。
- h – l当日股价范围，即当日最高价和最低价之差。
- h – previousclose 当日最高价和前一个交易日收盘价之差。
- previousclose – l 前一个交易日收盘价和当日最低价之差。

• (3) max函数返回数组中的最大值。基于上面计算的3个数值，我们来计算所谓的真实波动幅度，也就是这三者的最大值。现在我们想在一组数组之间按照元素挑选最大值——也就是在所有的数组中第一个元素的最大值、第二个元素的最大值等。为此，需要用NumPy中的maximum函数，而不是max函数。

truerange = np.maximum(h - l, h - previousclose, previousclose - l) 

• (4) 创建一个长度为N的数组atr，并初始化数组元素为0。

atr = np.zeros(N)

• (5) 这个数组的首个元素就是truerange数组元素的平均值。
  atr[0] = np.mean(truerange)

用如下公式计算其他元素的值：

这里，PATR表示前一个交易日的ATR值， TR即当日的真实波动幅度。

for i in range(1, N):
    atr[i] = (N - 1) * atr[i - 1] + truerange[i]
    atr[i] /= N

小结

我们生成了3个数组，分别表示3种范围——当日股价范围，当日最高价和前一个交易日收盘价之差，以及前一个交易日收盘价和当日最低价之差。这告诉我们股价波动的范围，也就是波动性的大小。 ATR的算法要求我们找出三者的最大值。而之前使用的max函数只能给出一个数组内的最大元素值，并非这里所需要的。我们要在一组数组之间挑选每一个元素位置上的最大值，也就是在所有的数组中第一个元素的最大值、第二个元素的最大值等。在这一节的“动手实践”教程中，我们了解到maximum函数可以做到这一点。最终，我们根据每一天的真实波动幅度值计算出一个移动平均值。完整代码如下：

import numpy as np
import sys

h, l, c = np.loadtxt('data.csv', delimiter=',', usecols=(4, 5, 6), unpack=True)

# N = int(sys.argv[1])
N = 20
h = h[-N:]
l = l[-N:]

print( "len(h)", len(h), "len(l)", len(l))
print( "Close", c)
previousclose = c[-N -1: -1]

print( "len(previousclose)", len(previousclose))
print( "Previous close", previousclose)
truerange = np.maximum(h - l, h - previousclose, previousclose - l) 

print( "True range", truerange)

atr = np.zeros(N)

atr[0] = np.mean(truerange)

for i in range(1, N):
    atr[i] = (N - 1) * atr[i - 1] + truerange[i]
    atr[i] /= N

print( "ATR", atr)

3.19 简单移动平均线

简单移动平均线（simple moving average）通常用于分析时间序列上的数据。为了计算它，我们需要定义一个N个周期的移动窗口，在我们的例子中即N个交易日。我们按照时间序列滑动这个窗口，并计算窗口内数据的均值。

3.20 动手实践：计算简单移动平均线

移动平均线只需要少量的循环和均值函数即可计算得出，但使用NumPy还有更优的选择——convolve函数。简单移动平均线只不过是计算与等权重的指示函数的卷积，当然，也可以是不等权重的。

卷积是分析数学中一种重要的运算，定义为一个函数与经过翻转和平移的另一个函数的乘积的积分。

按照如下步骤计算简单移动平均线。

• (1) 使用ones函数创建一个长度为N的元素均初始化为1的数组，然后对整个数组除以N，即可得到权重。如下所示：

import numpy as np
import matplotlib.pyplot as plt

N = 5
weights = np.ones(N) / N
print("Weights", weights)

在N = 5时，输出结果如下：

Weights [ 0.2 0.2 0.2 0.2 0.2]

• (2) 使用这些权重值，调用convolve函数：

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]

• (3) 我们从convolve函数返回的数组中，取出中间的长度为N的部分（即两者做卷积运算时完全重叠的区域）。下面的代码将创建
  一个存储时间值的数组，并使用Matplotlib进行绘图。

t = np.arange(N - 1, len(c))
plt.plot(t, c[N-1:], lw=1.0)
plt.plot(t, sma, lw=2.0)
plt.show()

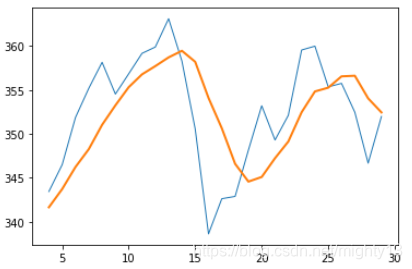
相对较平滑的粗线描绘的是5日移动平均线，而锯齿状的细线描绘的是每天的收盘价。

小结

我们计算出了收盘价数据的简单移动平均线。是的，你掌握了很重要的知识，那就是简单移动平均线可以用信号处理技术求解——与1/N的权重进行卷积运算，N为移动平均窗口的大小。我们还学习了ones函数的用法，即可以创建元素均为1的数组，以及convolve函数，计算一组数据与指定权重的卷积。

示例完整代码如下：

import numpy as np
import matplotlib.pyplot as plt

N = 5

weights = np.ones(N) / N
print("Weights", weights)

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))

plt.plot(t, c[N-1:], lw=1.0)
plt.plot(t, sma, lw=2.0)

plt.show()

3.21 指数移动平均线

除了简单移动平均线，指数移动平均线（exponential moving average）也是一种流行的技术指标。指数移动平均线使用的权重是指数衰减的。对历史上的数据点赋予的权重以指数速度减小，但永远不会到达0。我们将在计算权重的过程中学习exp和linspace函数。

3.22 动手实践：计算指数移动平均线

给定一个数组，exp函数可以计算出每个数组元素的指数。例如，看下面的代码：

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(5)
print( "Exp", np.exp(x))

输出结果如下：

Exp [ 1. 2.71828183 7.3890561 20.08553692 54.59815003]

linspace函数需要一个起始值和一个终止值参数，以及可选的元素个数的参数，它将返回一个元素值在指定的范围内均匀分布的数组。如下所示：

print( "Linspace", np.linspace(-1, 0, 5))

输出结果如下：

Linspace [-1. -0.75 -0.5 -0.25 0. ]

下面我们来对示例数据计算指数移动平均线。

• (1) 还是回到权重的计算——这次使用exp和linspace函数。

N = 5
weights = np.exp(np.linspace(-1. , 0. , N))

• (2) 对权重值做归一化处理。我们将用到ndarray对象的sum方法。

weights /= weights.sum()
print("Weights", weights)

在N = 5时，我们得到的权重值如下：

Weights [ 0.11405072 0.14644403 0.18803785 0.24144538 0.31002201]

• (3) 接下来就很容易了，我们只需要使用在简单移动平均线一节中学习到的convolve函数即可。同样，我们还是将结果绘制出来。

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
ema = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
plt.plot(t, c[N-1:], lw=1.0)
plt.plot(t, ema, lw=2.0)
plt.show()

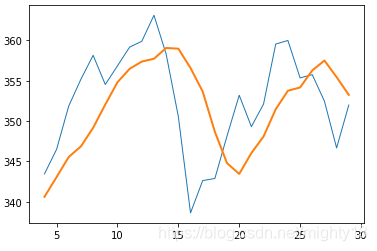
我们再次得到了曼妙的折线图。与之前一样，相对比较平滑的粗线描绘的是指数移动平均线，而锯齿状的细线描绘的是每天的收盘价。

小结

我们对收盘价数据计算了指数移动平均线。首先，我们使用exp和linspace函数计算出指数衰减的权重值。linspace函数返回的是一个元素值均匀分布的数组，随后我们计算出它们的指数。为了将这些权重值归一化，我们调用了ndarray对象的sum方法。最后，我们再次应用了在前面简单移动平均线一节中学习到的convolve函数，最终计算出指数移动平均线。

示例完整代码如下：

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(5)
print( "Exp", np.exp(x))
print( "Linspace", np.linspace(-1, 0, 5))

weights = np.exp(np.linspace(-1., 0., N))
weights /= weights.sum()
print( "Weights", weights)

N = 5

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
ema = np.convolve(weights, c)[N-1:-N+1]
t = np.arange(N - 1, len(c))
plt.plot(t, c[N-1:], lw=1.0)
plt.plot(t, ema, lw=2.0)
plt.show()

3.23 布林带

布林带（Bollinger band）又是一种技术指标。是的，股票市场的确有成千上万种技术指标。布林带是以发明者约翰·布林格（John Bollinger）的名字命名的，用以刻画价格波动的区间。布林带的基本型态是由三条轨道线组成的带状通道（中轨和上、下轨各一条）。

• 中轨：简单移动平均线。
• 上轨：比简单移动平均线高两倍标准差的距离。这里的标准差是指计算简单移动平均线所用数据的标准差。
• 下轨：比简单移动平均线低两倍标准差的距离。

3.24 动手实践：绘制布林带

我们已经掌握了计算简单移动平均线的方法。如有需要，请复习3.20节 动手实践：计算简单移动平均线”的内容。接下来的例子将介绍NumPy中的fill函数。fill函数可以将数组元素的值全部设置为一个指定的标量值，它的执行速度比使用array.flat = scalar或者用循环遍历数组赋值的方法更快。按照如下步骤绘制布林带。

• (0) 构建sma

import numpy as np
import matplotlib.pyplot as plt

N = 5

weights = np.ones(N) / N
print("Weights", weights)

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]

• (1) 我们已经有一个名为sma的数组，包含了简单移动平均线的数据。因此，我们首先要遍历和这些值有关的数据子集。数据子集构建完成后，计算其标准差。注意，从某种意义上来说，我们必须去计算每一个数据点与相应平均值之间的差值。如果不使用NumPy，我们只能遍历所有的数据点并逐一减去相应的平均值。幸运的是， NumPy中的fill函数可以构建元素值完全相同的数组。这可以让我们省去一层循环，当然也就省去了这个循环内作差的步骤。

deviation = []
C = len(c)

for i in range(N - 1, C):
    if i + N < C:
        dev = c[i: i + N]
    else:
        dev = c[-N:]
   
    averages = np.zeros(N)
    averages.fill(sma[i - N - 1])
    dev = dev - averages 
    dev = dev ** 2
    dev = np.sqrt(np.mean(dev))
    deviation.append(dev)

deviation = 2 * np.array(deviation)
print(len(deviation), len(sma))
upperBB = sma + deviation
lowerBB = sma - deviation

c_slice = c[N-1:]
between_bands = np.where((c_slice < upperBB) & (c_slice > lowerBB))

print(lowerBB[between_bands])
print(c[between_bands])
print(upperBB[between_bands])
between_bands = len(np.ravel(between_bands))
print("Ratio between bands", float(between_bands)/len(c_slice))

• (2) 使用如下代码绘制布林带。

t = np.arange(N - 1, C)
plt.plot(t, c_slice, lw=1.0)
plt.plot(t, sma, lw=2.0)
plt.plot(t, upperBB, lw=3.0)
plt.plot(t, lowerBB, lw=4.0)
plt.show()

下图是用我们的示例数据绘制出来的布林带。中间锯齿状的细线描绘的是每天的收盘价，而稍微粗一点也平滑一点的穿过它的曲线即为简单移动平均线。

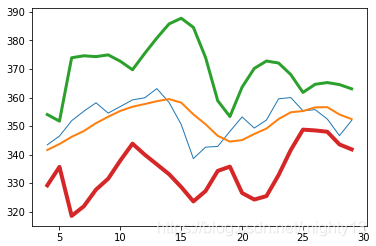
小结

我们在示例数据上计算得到了布林带。更重要的是，我们还了解了NumPy中fill函数的用法。该函数可以用一个指定的标量值填充数组，而这个标量值也是fill函数唯一的参数。

示例完整代码如下：

import numpy as np
import matplotlib.pyplot as plt

N = 5

weights = np.ones(N) / N
print("Weights", weights)

c = np.loadtxt('data.csv', delimiter=',', usecols=(6,), unpack=True)
sma = np.convolve(weights, c)[N-1:-N+1]
deviation = []
C = len(c)

for i in range(N - 1, C):
    if i + N < C:
        dev = c[i: i + N]
    else:
        dev = c[-N:]
   
    averages = np.zeros(N)
    averages.fill(sma[i - N - 1])
    dev = dev - averages 
    dev = dev ** 2
    dev = np.sqrt(np.mean(dev))
    deviation.append(dev)

deviation = 2 * np.array(deviation)
print(len(deviation), len(sma))
upperBB = sma + deviation
lowerBB = sma - deviation

c_slice = c[N-1:]
between_bands = np.where((c_slice < upperBB) & (c_slice > lowerBB))

print(lowerBB[between_bands])
print(c[between_bands])
print(upperBB[between_bands])
between_bands = len(np.ravel(between_bands))
print("Ratio between bands", float(between_bands)/len(c_slice))
t = np.arange(N - 1, C)

plt.plot(t, c_slice, lw=1.0)
plt.plot(t, sma, lw=2.0)
plt.plot(t, upperBB, lw=3.0)
plt.plot(t, lowerBB, lw=4.0)

plt.show()