[个人学习博客]时间序列分析的统计检验

时间序列分析主要包括三个检验：白噪声检验，平稳性检验和时间序列数据的自相关系数和偏自相关系数的分析

# 一些导入的准备工作

"""
主要参考书籍:孙玉林,余本国.2021年9月.Python机器学习算法与实战.电子工业出版社
"""
# 导入科学运算和绘图的包
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
# 输出高清图像
%config InlineBackend.figure_format="retina"
%matplotlib inline
sns.set(font="Kaiti",style="ticks",font_scale=1.4) # 规范sns输出的图片格式
# 解决显示中文的问题
plt.rcParams['axes.unicode_minus'] = False 
plt.rcParams["font.sans-serif"] = ["SimHei"]

# 生成实验数据

# 生成随机数据,用于实验(X1为非随机化数据,X2为随机化数据)
# 设置随机数种子以确保结果的可复现性  
np.random.seed(42)    
# 设置时间序列的长度  
length = 100  
# 生成时间序列索引  
dates = pd.date_range(start='2023-01-01', periods=length, freq='D')  
# 生成带有线性趋势的X1序列数据  
slope = 0.1  # 线性趋势的斜率  
intercept = 10  # 线性趋势的截距  
X1_trend = slope * np.arange(length) + intercept  
X1 = X1_trend + np.random.randn(length)  # 在趋势基础上添加随机噪声  
  
# 生成完全随机的X2序列数据  
X2 = np.random.randn(length) + 14
  
# 将数据组合成DataFrame  
df = pd.DataFrame({'date': dates, 'X1': X1, 'X2': X2})  
df['date'] = pd.to_datetime(df['date'])  
df = df.set_index('date')  

# 数据可视化

df.head()
# 可视化时间序列数据
df.plot(kind="line",figsize=(10,6))
plt.grid() # 添加网格线
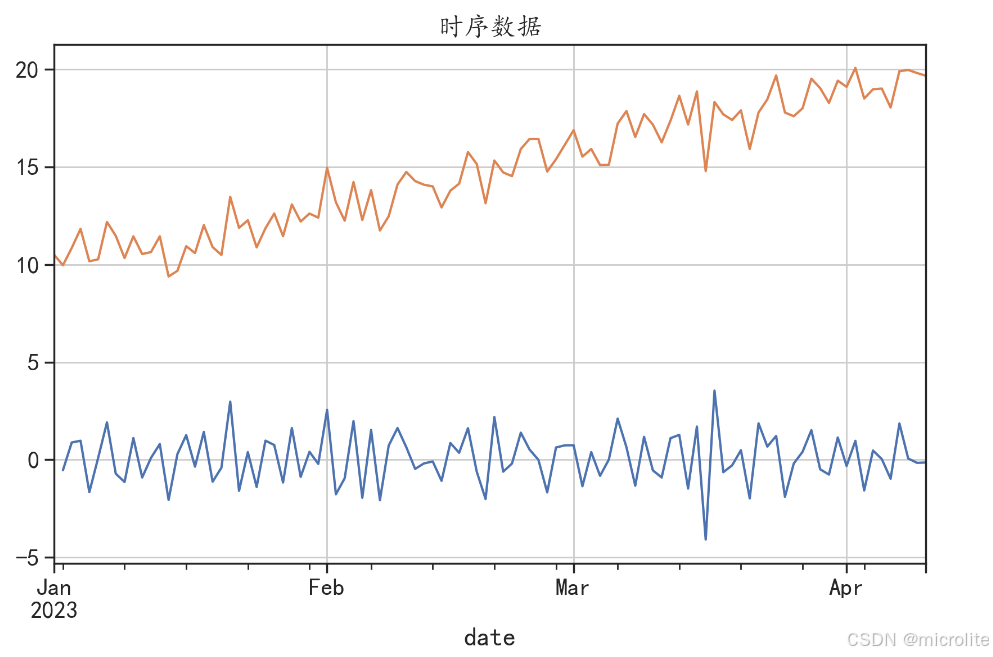
plt.title("时序数据")
plt.show()

# 白噪声检验

如果一个序列是白噪声(独立同分布的随机数据),那么进行时间序列分析是无意义的。因此需要进行白噪声检验

常用的检验方法为LB检验（Ljung-Box检验）

H0：延迟期数小于或等于m期的序列之间相互独立（序列为白噪声）

H1：延迟期数小于或等于m期的序列之间存在相关性（序列不为白噪声）

利用sm.stats.diagnostic.acorr_ljungbox()进行白噪声检验

## LB检验
import statsmodels.api as sm
lags = [4,8,16,32] #m
LB = sm.stats.diagnostic.acorr_ljungbox(df["X1"],lags=lags,return_df=True)
print("序列X1的检验结果:\n",LB)
LB = sm.stats.diagnostic.acorr_ljungbox(df["X2"],lags=lags,return_df=True)
print("序列X2的检验结果:\n",LB)

检验结果如下：

根据LB检验的结果，在延迟阶数[4,8,16,32]的情况下,X1序列P值均小于0.05,拒绝H0,接受H1,差异有统计学意义，认为该数据不是随机的。同理，认为X2是随机的。

# 平稳性检验

判断平稳性对于选择预测的数学模型十分关键,如果平稳则可以直接使用ARMA(自回归移动平均模型),如果不平稳则要尝试建立ARIMA(差分移动自回归平均模型) # 之后会写一篇博客详细讲这两个方法

判断平稳的方法常用的有三种,包括时序图主观判断、ADF检验和KPSS检验:

### 平稳性检验
## 方法1:根据时序图和自相关图显示的特征做判断
df.plot(kind='line',figsize=(10,6))
plt.grid()
plt.title("时序数据")
plt.show()
## 方法2:构造检验统计量进行假设检验
# 常用方法为ADF检验,检验时间序列中单位根的存在性(H0:序列是非平稳的(序列有单位根))
from statsmodels.tsa.stattools import *  # 导入检验统计方法
dftest = adfuller(df["X2"],autolag="BIC")
dfoutput = pd.Series(dftest[0:4],index=["adf","p-value","usedlag","Number of Observations Used"])
print("X2单位根检验结果:\n",dfoutput)
dftest = adfuller(df["X1"],autolag='BIC')
dfoutput = pd.Series(dftest[0:4],index=["adf","p-value","usedlag","Number of Observations Used"])
print("X1单位根检验结果:\n",dfoutput)
## 对X1一阶差分后的序列进行检验
X1diff = df["X1"].diff().dropna() # 一阶差分
dftest = adfuller(X1diff,autolag = 'BIC')
dfoutput = pd.Series(dftest[0:4],index=["adf","p-value","usedlag","Number of Observations Used"])
print("X1一阶差分单位根检验结果:\n",dfoutput)

第一种方法就是看上面已经做出来的时序图,主观性很强,所以一般选用ADF检验,运行结果如下:

根据P值判断,X2小于0.05,说明X2为平稳时间序列

X1的P值为0.94,远大于0.05,认为X1为不平稳序列,进一步进行差分,使其平稳

差分后,X1一阶差分的P值小于0.05,认为X1一阶差分为平稳序列

 X1差分前后的时序图如下:

X1diff.plot(kind='line',figsize=(10,6))
df["X1"].plot(kind='line',figsize=(10,6))
plt.grid()
plt.title("时序数据")
plt.show()

## 方法三：KPSS检验
# H0：检测的序列是平稳的
# 对序列X2使用KPSS检验平稳性
dfkpss = kpss(df["X2"])
dfoutput = pd.Series(dfkpss[0:3],index=["kpss_stat","p-value","usedlag"])
print("X2 KPSS检验结果：\n",dfoutput)
# 对序列X1使用KPSS检验平稳性
dfkpss = kpss(df["X1"])
dfoutput = pd.Series(dfkpss[0:3],index=["kpss_stat","p-value","usedlag"])
print("X1 KPSS检验结果：\n",dfoutput)
# 对一阶差分X1使用KPSS检验平稳性
dfkpss = kpss(X1diff)
dfoutput = pd.Series(dfkpss[0:3],index=["kpss_stat","p-value",'usedlag'])
print("X1一阶差分KPSS检验结果:\n",dfoutput)

输出结果如下：

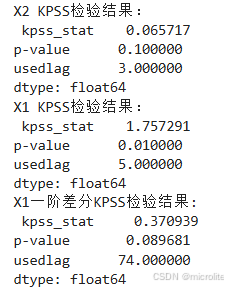
X2的P值大于0.05，认为其是平稳的；X1的P值小于0.05，认为其是不平稳的；一阶差分X1的P值大于0.05，认为其实平稳的

报错解释：因为KPSS检验计算得到的P值范围是0.1~0.01，所以X1的实际P值小于0.01，X2的实际P值大于0.1，只是无法显示。

针对时间序列ARIMA(p,d,q)模型，参数d可以通过差分次数来确定:

## 针对时间序列ARIMA(p,d,q)模型
# 检验ARIMA模型的参数d
from statsmodels.tsa.api import SimpleExpSmoothing, Holt, ExponentialSmoothing, AR, ARIMA
import pmdarima as pm
X1d=pm.arima.ndiffs(df["X1"],alpha = 0.05,test="kpss",max_d=3)
print("使用KPSS检验对序列X1的参数d取值进行预测,d=",X1d)

X1diffd = pm.arima.ndiffs(X1diff,alpha = 0.05,test = "kpss",max_d=3)
print("使用KPSS检验对序列X1一阶差分后的参数d取值进行预测,d=",X1diffd)

X2d=pm.arima.ndiffs(df["X2"],alpha=0.05,test="kpss",max_d=3)
print("使用KPSS检验对序列X2的参数d取值进行预测,d=",X2d)