为什么要有激活函数?
因为假设没有激活函数,神经网络会退化成单层的矩阵运算,激活函数确保它有复杂的表达能力.
为什么要增加层数?
中间层神经网络会自主学习到重要的信息,表达能力增强.
最小化误差:
梯度下降(a 学习率):
梯度下降法会陷入局部最优解,但由于神经网络参数量较大,故不容易出现这种情况
学习率较小会走得慢,学习率太大会震荡不达到最优解.
反向传播
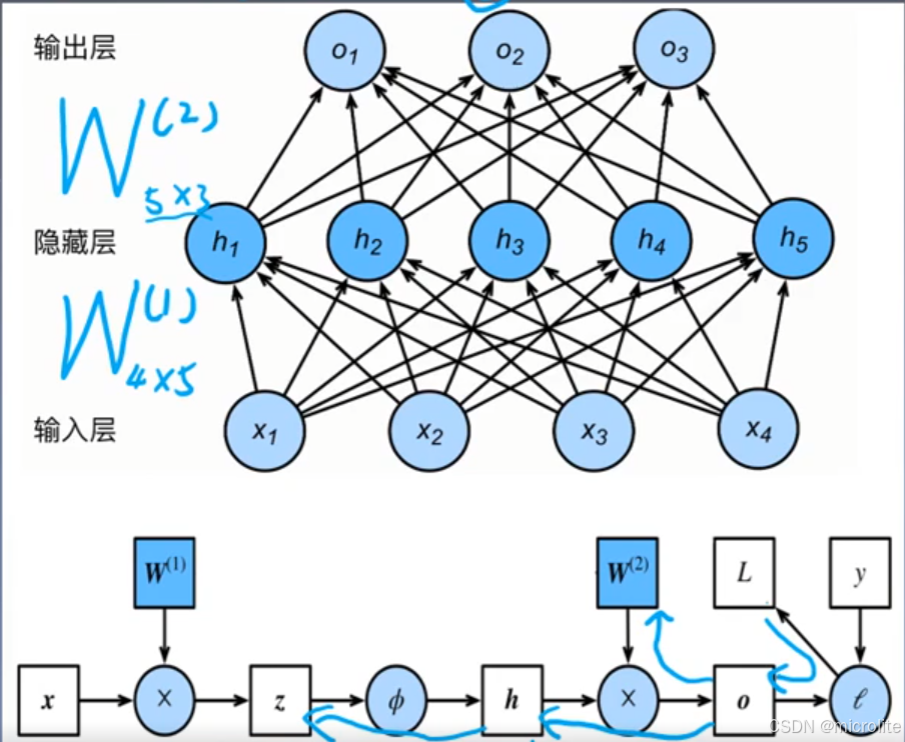
每一个偏导数都用到了上一级的偏导数
有几条通路就有几项进行相加
为什么要有激活函数?
因为假设没有激活函数,神经网络会退化成单层的矩阵运算,激活函数确保它有复杂的表达能力.
为什么要增加层数?
中间层神经网络会自主学习到重要的信息,表达能力增强.
最小化误差:
梯度下降(a 学习率):
梯度下降法会陷入局部最优解,但由于神经网络参数量较大,故不容易出现这种情况
学习率较小会走得慢,学习率太大会震荡不达到最优解.
反向传播

每一个偏导数都用到了上一级的偏导数
有几条通路就有几项进行相加
 2615
2615
 3072
3072
 588
588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


