期权专题8：隐含波动率（BSM二分法）

目录

1. 定义及方法

1.1 隐含波动率

1.2 BSM二分法

2. 代码实现

2.1. 数据获取

2.2 计算数值

2.3 批量测算及作图

 2.4 完整代码

  3. 总结

---

免责声明：本文由作者参考相关资料，并结合自身实践和思考独立完成，对全文内容的准确性、完整性或可靠性不作任何保证。同时，文中提及的数据仅作为举例使用，不构成推荐；文中所有观点均不构成任何投资建议。请读者仔细阅读本声明，若读者阅读此文章，默认知晓此声明。

1. 定义及方法

1.1 隐含波动率

      隐含波动率（简称隐波）是将期权实际的市价带入BSM模型，反推出来的数值。隐波反映了整个市场参与者对于对于未来不确定性或风险水平的预期。如果隐波的数值较前期上涨，说明大家预期未来市场波动将会增大，反之则减小。

1.2 BSM二分法

     基于BSM模型计算隐波的方法有多种（各种方式测算出的结果差异均不大，不再逐一介绍），本文主要选择二分法。选择二分法的原因主要有两点：1.思路简单，理解起来比较容易；2.速度较快，同时精准度也较高。

     BSM计算期权价格时采用的波动率是常数，隐波的求解其实就是在已知期权价格的情况下反解波动率的值。由于BSM的公式比较复杂，所以使用解析法难度比较高，因此选择模拟法的思路来求解。模拟法的思路是：在BSM模型中传入不同的波动率数值，当计算得出的期权价格等于实际市价的时候，对应的波动率即是该期权当前的隐含波动率。

     由于模拟法本身需要大量的数据进行循环，因此在模拟法的基础上叠加‘夹逼定理’的思路，即采用二分法来降低模拟循环的次数，提高运算的效率。下面，使用一个流程图来展示BSM二分法的思路和步骤：

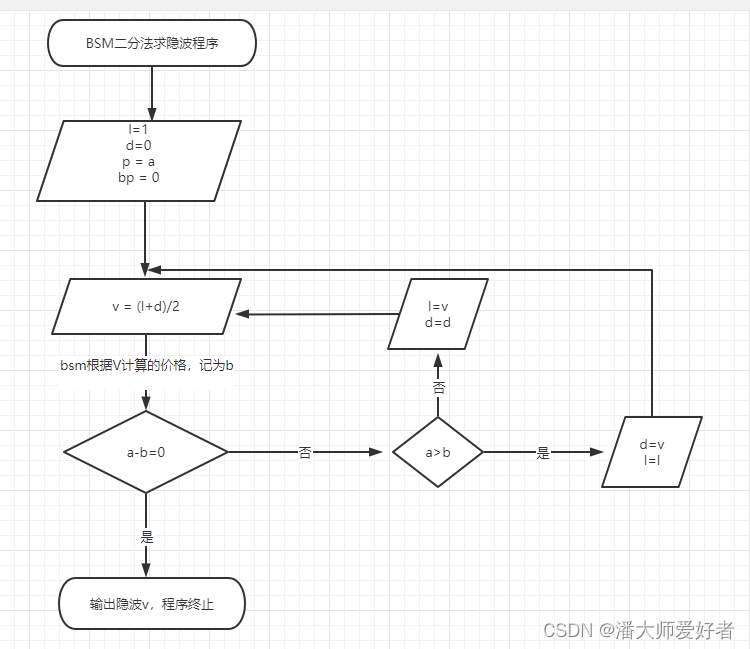
    上图中,l表示波动率上限，初始值为1；d表示波动率，下限初始值为0。p表示期权真实市价，值为a,bp表示BSM模型计算出的期权价格，初始值为0。v表示传入的波动率值。其他的BSM模型所需参数根据期权要素设置为定参，此处不再传入。

    根据流程，初始传入的V值为0.5（上限1和下限0的均值），根据V值BSM模型计算出的价格bp值为b。如果a和b的值相等，则说明V为期权对应的隐含波动率，程序结束

    如果啊a,b不相等，则需要继续寻找波动率的合适值。若a>b,说明BSM测算出来的值偏低，即设置的波动率偏低，真实的波动率应该大于0.5，将波动率下限d设置为0.5，上限任然不变，此时对应的新的波动率为0.75，传入原流程继续循环。 同样地，若a<b,说明BSM测算出来的值偏高，即设置的波动率偏高，真实的波动率应该小于0.5，将波动率上限l设置为0.5，下限保持不变，此时对应的新的波动率为0.25，传入原流程继续循环。

   需要注意的是，实际过程中程序测算的b值可能是无限小数，因此在值的大小比较上，应该将a=b的条件切换为|a-b|<c,即二者差的绝对值小于一个误差值c,c值可以取0.0001，c值决定了误差的精度，其取值因所需而异。

2. 代码实现

2.1. 数据获取

    由于需要使用到BSM模型，因此先放一下前期写的BSM模型的代码（对此处不太熟悉的读者可以查看前期的文章期权专题6），代码如下：

import akshare as ak
import numpy as np
from scipy.stats import norm
import pandas as pd


def get_constant_value(in_value, fix_value):
    # 当参数数值未传入时，取默认值
    if in_value == None:
        out_value = fix_value
    else:
        out_value = in_value
    return out_value

def BSM_option_price(d_type, S = None, K = None, vol = None, T = None, r = None ):
    '''
    BSM-期权定价模型
    ----------
    d_type:str,期权类型，call/put
    S:float,标的资产价格，默认值为100
    K:float,行权价格，默认值为120
    vol:float,年化波动率，默认值为0.2
    T:float,剩余期限（折算成年），默认值为0.5
    r:float,连续复利无风险利率，默认值为0.03
    -------
    '''
    S1 = get_constant_value(S, 100)
    K1 = get_constant_value(K, 120)
    vol1 = get_constant_value(vol, 0.2)
    T1 = get_constant_value(T, 0.5)
    r1 = get_constant_value(r, 0.03)

    value = v