文章介绍了H_M模型在基金净值归因中的作用，用于评估基金的选股和择时收益。通过线性回归分析，展示了模型如何计算选股能力（阿尔法）和择时能力（贝塔1和贝塔2）。实际案例以一只500增强基金为例，展示了数据获取、模型构建及结果分析过程，指出该基金在2022年的选股能力正向、择时能力负向。文章强调模型的局限性和适用范围，并提醒读者结果仅供参考，不构成投资建议。
目录
免责声明：本文由作者参考相关资料，并结合自身实践和思考独立完成，对全文内容的准确性、完整性或可靠性不作任何保证。同时，文中提及的基金仅作为举例使用，不构成推荐；文中所有观点均不构成任何投资建议。请读者仔细阅读本声明，若读者阅读此文章，默认知晓此声明。
1. 模型介绍
1.1 模型公式
H_M模型是在CAPM模型，T_M模型的基础上，进行迭代的基金净值归因类模型，主要用于评价基金的选股收益和择时收益。T_M模型在CAPM的基础上增加了市场风险溢价的二次项，以二次项的回归系数（贝塔2）来判断投资经理的择时能力。H_M模型在T_M模型的基础上增加了二次项的虚拟变量，以引入虚拟变量后的二次项的回归系数（贝塔2）来判断投资经理的择时能力。而后续的C_L模型采取了双虚拟变量的回归方程，其本质上和H_M是等价的。H_M模型相比T_M模型有进一步的优化，在理解层面和表达式层面相对C_L模型简洁。因此，本文选择其作为介绍对象。
H_M模型表达式（二元线性回归方程）如下：
1.2 模型使用
截距项的阿尔法的值表示的是选股能力，这一点和CAPM模型一样。因此阿尔法的值越大，说明投资组合的选股能力越强；反之则越弱。
对于回归系数贝塔1和贝塔2，可以理解为：当市场下跌时，投资组合对应的贝塔值为贝塔1,；当市场上涨时，投资组合上调贝塔值，此时对应的贝塔值为贝塔1和贝塔2的和。因此，如果贝塔2的值大于零，说明投资组合在市场上涨的情况下加仓，是主动择时且表现，且值越大，择时能力体现的越强；反之若贝塔2的值小于零，说明择时能力较差。
值得注意的是，如果单看某一时间点的阿尔法值和贝塔2值，得出的结论相对是不准确的。因此需要观测二者的时序累计走势，提高评价的准确性。
2. 实际案例
2.1 获取数据
本文以一只500增强基金005965（后续简称a基金）作为案例，时间节点选择2022年整年。首先使用akshare开源api，获取中证500指数和a基金在2022年的日度收益率（百分比收益率）数据，假设无风险利率为年化1%，整体的代码如下：
import akshare as ak
import pandas as pd
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
def get_data(index_code, fund_code, start_day, end_day):
'''
获取回归所需的变量
----------
index_code:str,指数代码，格式如'sh000905'
fund_code:str,基金代码，格式如‘000001’
start_day:str，开始日期，格式如'2022-12-01'
end_day:str，结束日期，格式如'2022-12-01'
Returns: DataFrame
-------
'''
# 获取净值数据，合并表格
index_df = ak.stock_zh_index_daily_em(symbol=index_code).sort_values(by=['date'], ascending=True)
fund_df = ak.fund_open_fund_info_em(fund=fund_code, indicator="累计净值走势")
fund_df['date'] = fund_df['净值日期'].apply(lambda x: pd.to_datetime(x).strftime("%Y-%m-%d"))
new_index = index_df.loc[(index_df['date'] >= start_day) & (index_df['date'] <= end_day)]
new_fund = fund_df.loc[(fund_df['date'] >= start_day) & (fund_df['date'] <= end_day)]
me_df = pd.merge(new_index, new_fund, on='date', how='inner')
# 计算收益率（第一行收益率为0，处理后需过滤）,合成新的表格
r_f = 0.01 / 365 # 无风险利率折算到每天
me_df['index_re'] = me_df['close'].pct_change().fillna(0)
me_df['fund_re'] = me_df['累计净值'].pct_change().fillna(0)
new_me = me_df.iloc[1::]
out_df = pd.DataFrame({'date': new_me['date'], 'rm': new_me['index_re'],
'rp': new_me['fund_re']})
# 合成线性回归所需表格
out_df['(rm-rf)'] = out_df['rm'] - r_f
out_df['(rp-rf)'] = out_df['rp'] - r_f
out_df['(rm-rf)**2'] = out_df['(rm-rf)'].apply(lambda x: x ** 2 if x >= 0 else 0)
return out_df
if __name__ == '__main__':
index_code = 'sh000905'
fund_code = '005965'
start_day = '2021-12-31'
end_day = '2022-12-30'
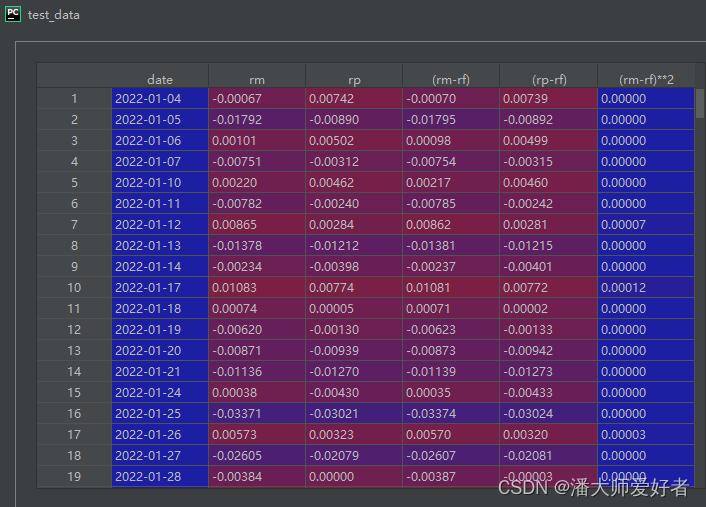
test_data = get_data(index_code, fund_code, start_day, end_day)得到的结果如图：
2.2 线性回归
在out_df的基础上，建立全量数据（日期从初始到终止）的回归方程，并得到对应的结果，代码如下：
def get_result(date, data_x, data_y):
'''
获取线性回归的结果
----------
终止日:str，开始日期，格式如'2022-12-01'
data_x:ndarray, 自变量矩阵
data_y:ndarray, 因变量矩阵
Returns: DataFrame
-------
'''
model = LinearRegression()
new_model = model.fit(data_x, data_y)
beta1 = new_model.coef_[0]
beta2 = new_model.coef_[1]
alpha = new_model.intercept_
R = model.score(data_x, data_y)
out_df = pd.DataFrame({'日期': [date], 'beta1': [round(beta1, 4)], 'beta2': [round(beta2, 4)],'alpha': [round(alpha, 4)], 'R^2': [round(R, 4)]})
return out_df
if __name__ == '__main__':
index_code = 'sh000905'
fund_code = '005965'
start_day = '2021-12-31'
end_day = '2022-12-30'
test_data = get_data(index_code, fund_code, start_day, end_day)
data_x = np.array(test_data.loc[:, ['(rm-rf)', '(rm-rf)**2']])
data_y = np.array(test_data['(rp-rf)'])
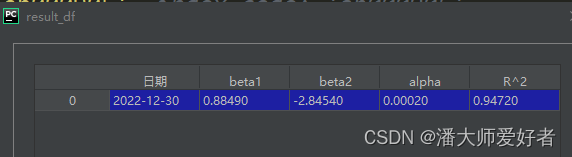
result_df = get_result(end_day, data_x, data_y)得到的结果如下图：
2.3 获取时序结果
前文例举了单个时间段的模型结果，由于单个时间段的结果存在不确定性，因此我们需要考虑多个时间段的时序结果。接下来，固定起始日，更换截止日，采用循环测算相应的时序结果，考虑到数据样本量对模型效果的影响，本文选择以4月初作为截止日的起点。代码如下：
if __name__ == '__main__':
index_code = 'sh000905'
fund_code = '005965'
start_day = '2021-12-31'
end_day = '2022-12-30'
test_data = get_data(index_code, fund_code, start_day, end_day)
last_df = pd.DataFrame()
for num in range(66,len(test_data)+1):
new_data = test_data.iloc[:num:]
one_date = new_data['date'].max()
data_x = np.array(new_data.loc[:, ['(rm-rf)', '(rm-rf)**2']])
data_y = np.array(new_data['(rp-rf)'])
one_result_df = get_result(one_date, data_x, data_y)
last_df = last_df.append(one_result_df)得到的结果如下：
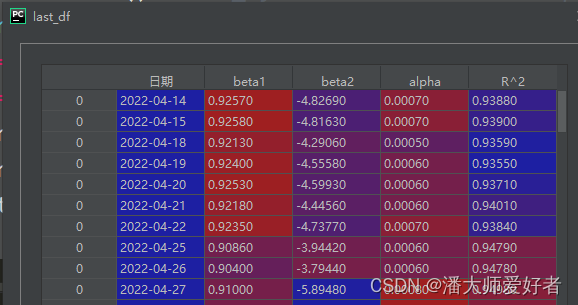
R^2表示的是可决系数，从图中可以看出可决系数基本在95%左右，说明模型的拟合效果不错。接下来，对得到的数据进行可视化操作。代码如下：
if __name__ == '__main__':
index_code = 'sh000905'
fund_code = '005965'
start_day = '2021-12-31'
end_day = '2022-12-30'
test_data = get_data(index_code, fund_code, start_day, end_day)
last_df = pd.DataFrame()
for num in range(66, len(test_data) + 1):
new_data = test_data.iloc[:num:]
one_date = new_data['date'].max()
data_x = np.array(new_data.loc[:, ['(rm-rf)', '(rm-rf)**2']])
data_y = np.array(new_data['(rp-rf)'])
one_result_df = get_result(one_date, data_x, data_y)
last_df = last_df.append(one_result_df)
# 作图
last_df['日期'] = pd.to_datetime(last_df['日期'])
zt = plt.figure()
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
name = last_df.columns.tolist()
for num in range(1, len(name)):
p = zt.add_subplot(2, 2, num)
new_name = name[num]
p.plot(last_df['日期'], last_df[new_name], label=new_name + '走势', color='orange')
plt.legend(loc='best')
plt.show()得到的结果如下图：
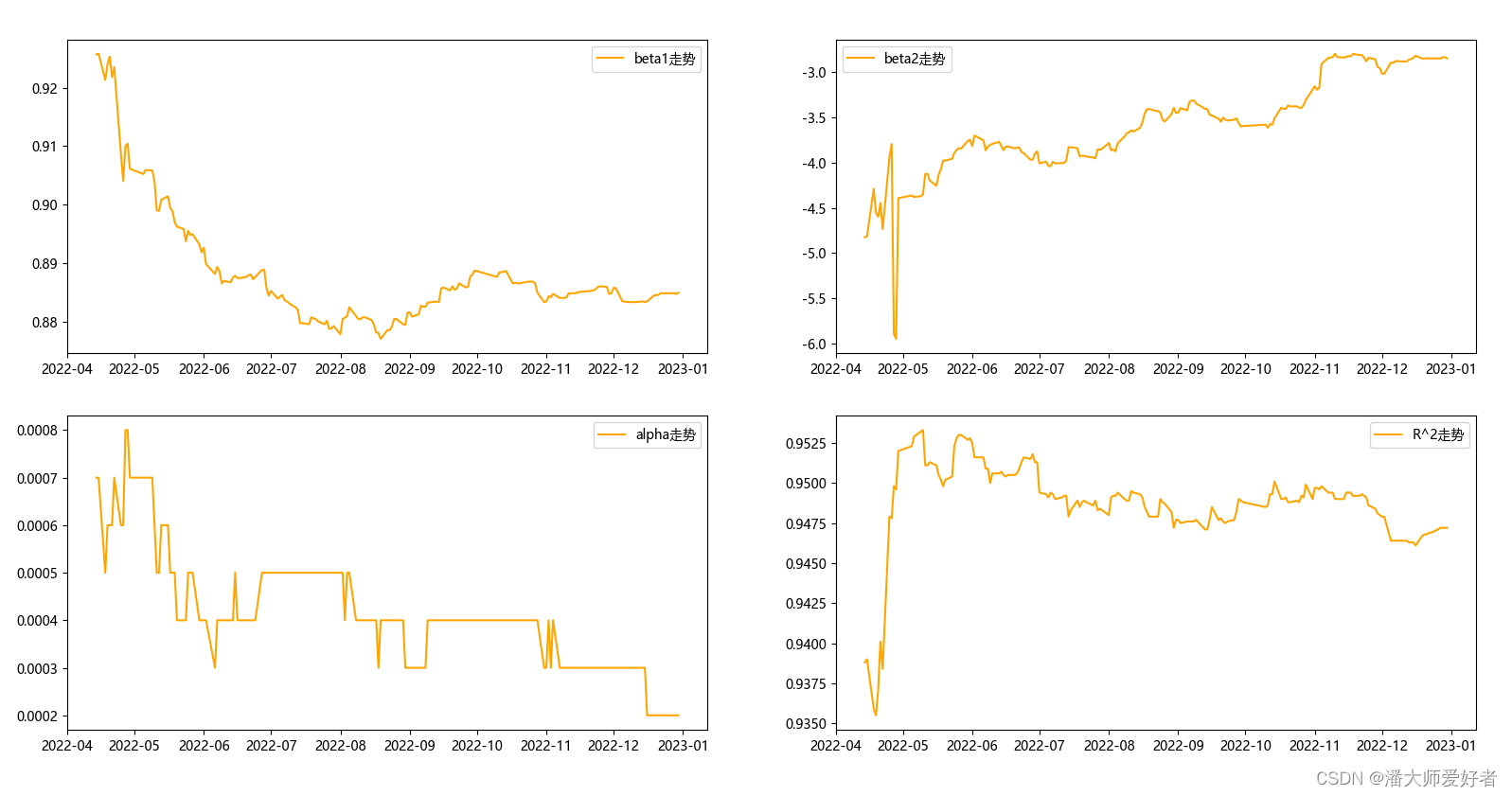
从beta1的走势可以看出，a基金自2022年初到8月份贝塔值一直在下降，9月份后贝塔值开始上升，后续保持几乎保持稳定。从beta2的走势可以看出，a基金的择时能力一直为负，只是陆续有所提升，最终贝塔2的值维持在-3附近。从alpha的走势可以看出，a基金的选股能力一直在下降，但最终保持着正向的选股能力。从R^2的走势可以看出，当数据样本量达到一定量后，R^2趋向于稳定在一个较小的区间内，从值可以看出，模型整体的回归效果较好，具备较好的解释性。
总结下来：2022全年，a基金具备正向的选股能力，负向的择时能力
*上述对基金的分析仅为举例的个人观点，不作为任何投资建议以及基金诊断结论，读者请注意。
2.4 完整代码
import akshare as ak
import pandas as pd
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
def get_data(index_code, fund_code, start_day, end_day):
'''
获取回归所需的变量
----------
index_code:str,指数代码，格式如'sh000905'
fund_code:str,基金代码，格式如‘000001’
start_day:str，开始日期，格式如'2022-12-01'
end_day:str，结束日期，格式如'2022-12-01'
Returns: DataFrame
-------
'''
# 获取净值数据，合并表格
index_df = ak.stock_zh_index_daily_em(symbol=index_code).sort_values(by=['date'], ascending=True)
fund_df = ak.fund_open_fund_info_em(fund=fund_code, indicator="累计净值走势")
fund_df['date'] = fund_df['净值日期'].apply(lambda x: pd.to_datetime(x).strftime("%Y-%m-%d"))
new_index = index_df.loc[(index_df['date'] >= start_day) & (index_df['date'] <= end_day)]
new_fund = fund_df.loc[(fund_df['date'] >= start_day) & (fund_df['date'] <= end_day)]
me_df = pd.merge(new_index, new_fund, on='date', how='inner')
# 计算收益率（第一行收益率为0，处理后需过滤）,合成新的表格
r_f = 0.01 / 365 # 无风险利率折算到每天
me_df['index_re'] = me_df['close'].pct_change().fillna(0)
me_df['fund_re'] = me_df['累计净值'].pct_change().fillna(0)
new_me = me_df.iloc[1::]
out_df = pd.DataFrame({'date': new_me['date'], 'rm': new_me['index_re'],
'rp': new_me['fund_re']})
# 合成线性回归所需表格
out_df['(rm-rf)'] = out_df['rm'] - r_f
out_df['(rp-rf)'] = out_df['rp'] - r_f
out_df['(rm-rf)**2'] = out_df['(rm-rf)'].apply(lambda x: x ** 2 if x >= 0 else 0)
return out_df
def get_result(date, data_x, data_y):
'''
获取线性回归的结果
----------
终止日:str，开始日期，格式如'2022-12-01'
data_x:ndarray, 自变量矩阵
data_y:ndarray, 因变量矩阵
Returns: DataFrame
-------
'''
model = LinearRegression()
new_model = model.fit(data_x, data_y)
beta1 = new_model.coef_[0]
beta2 = new_model.coef_[1]
alpha = new_model.intercept_
R = model.score(data_x, data_y)
out_df = pd.DataFrame(
{'日期': [date], 'beta1': [round(beta1, 4)], 'beta2': [round(beta2, 4)], 'alpha': [round(alpha, 4)],
'R^2': [round(R, 4)]})
return out_df
if __name__ == '__main__':
index_code = 'sh000905'
fund_code = '005965'
start_day = '2021-12-31'
end_day = '2022-12-30'
test_data = get_data(index_code, fund_code, start_day, end_day)
last_df = pd.DataFrame()
for num in range(66, len(test_data) + 1):
new_data = test_data.iloc[:num:]
one_date = new_data['date'].max()
data_x = np.array(new_data.loc[:, ['(rm-rf)', '(rm-rf)**2']])
data_y = np.array(new_data['(rp-rf)'])
one_result_df = get_result(one_date, data_x, data_y)
last_df = last_df.append(one_result_df)
# 作图
last_df['日期'] = pd.to_datetime(last_df['日期'])
zt = plt.figure()
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
name = last_df.columns.tolist()
for num in range(1, len(name)):
p = zt.add_subplot(2, 2, num)
new_name = name[num]
p.plot(last_df['日期'], last_df[new_name], label=new_name + '走势', color='orange')
plt.legend(loc='best')
plt.show()3. 模型评价
3.1 模型优点
1. 模型具有较强的逻辑性，同时具备较强的理论支撑。
2. 数据容易获取，且完整度较高，处理方式也比较常见。
3. 定量化的分析，结果的可靠性较强。
3.2 模型缺点
1. 结论受统计时间区间影响，不同区间结论可能存在差异（若使用结论的时序数据或者采取同期比较可有效优化）。
2. 仅适合具有比较基准的基金，使用范围有限（相对来说较为适合指数类以及指数增强类基金）。
3. 若基金偏离基准较大，模型存在较大概率的失效风险。
4. 模型考虑的影响因素较少，对于择时能力的界定较为粗糙。
免责声明：本文由作者参考相关资料，并结合自身实践和思考独立完成，对全文内容的准确性、完整性或可靠性不作任何保证。同时，文中提及的基金仅作为举例使用，不构成推荐；文中所有观点均不构成任何投资建议。请读者仔细阅读本声明，若读者阅读此文章，默认知晓此声明。
扫一扫
8032
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
