On the way to school, Karen became fixated on the puzzle game on her phone!

The game is played as follows. In each level, you have a grid with n rows and m columns. Each cell originally contains the number 0.
One move consists of choosing one row or column, and adding 1 to all of the cells in that row or column.
To win the level, after all the moves, the number in the cell at the i-th row and j-th column should be equal to gi, j.
Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!
The first line of input contains two integers, n and m (1 ≤ n, m ≤ 100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains gi, j (0 ≤ gi, j ≤ 500).
If there is an error and it is actually not possible to beat the level, output a single integer -1.
Otherwise, on the first line, output a single integer k, the minimum number of moves necessary to beat the level.
The next k lines should each contain one of the following, describing the moves in the order they must be done:
- row x, (1 ≤ x ≤ n) describing a move of the form "choose the x-th row".
- col x, (1 ≤ x ≤ m) describing a move of the form "choose the x-th column".
If there are multiple optimal solutions, output any one of them.
3 5 2 2 2 3 2 0 0 0 1 0 1 1 1 2 1
4 row 1 row 1 col 4 row 3
3 3 0 0 0 0 1 0 0 0 0
-1
3 3 1 1 1 1 1 1 1 1 1
3 row 1 row 2 row 3
In the first test case, Karen has a grid with 3 rows and 5 columns. She can perform the following 4 moves to beat the level:
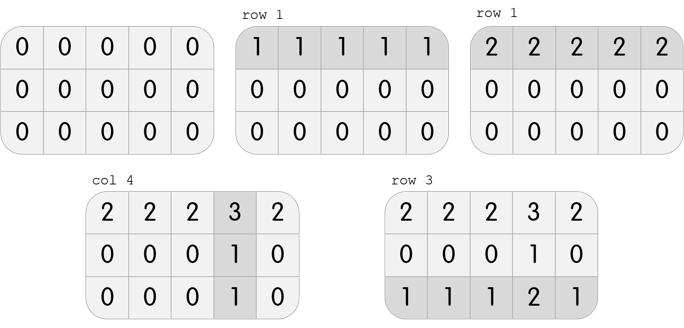
In the second test case, Karen has a grid with 3 rows and 3 columns. It is clear that it is impossible to beat the level; performing any move will create three 1s on the grid, but it is required to only have one 1 in the center.
In the third test case, Karen has a grid with 3 rows and 3 columns. She can perform the following 3 moves to beat the level:
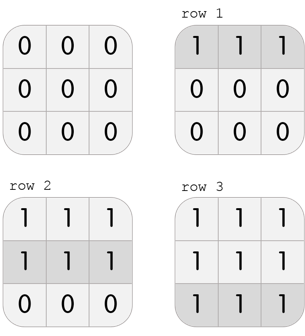
Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.
题目大意:
每次操作可以选择一行或者一列进行整体+1的操作,问最少步数,使得一开始的全0矩阵变成输入进来的N*M的矩阵。
思路:
直接模拟,先行后列的去做,每行取最小值,以及每列取最小值,那么就是这一行和这一列的操作数量。
对应模拟出来就行了。
因为是要最小步数,所以有可能要先列后行的去做,那么我们两种情况都做以下然后比较操作数量即可。
Ac代码(代码稍微有点挫):
#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
int c[150][150];
int d[150][150];
int ans[100000][3];
int ans2[100000][3];
int a[150][150];
int b[150][150];
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m))
{
int output=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
c[i][j]=a[i][j];
}
}
int cnt=0;
for(int i=1;i<=n;i++)
{
int minn=0x3f3f3f3f;
for(int j=1;j<=m;j++)
{
minn=min(minn,a[i][j]);
}
if(minn==0)continue;
output+=minn;
ans[cnt][0]=0;
ans[cnt][1]=i;
ans[cnt++][2]=minn;
for(int j=1;j<=m;j++)
{
b[i][j]+=minn;
a[i][j]-=minn;
}
}
for(int j=1;j<=m;j++)
{
int minn=0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
minn=min(minn,a[i][j]);
}
if(minn==0)continue;
output+=minn;
ans[cnt][0]=1;
ans[cnt][1]=j;
ans[cnt++][2]=minn;
for(int i=1;i<=n;i++)
{
b[i][j]+=minn;
a[i][j]-=minn;
}
}
int flag=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]!=0)flag=1;
}
}
if(flag==0)
{
int output2=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
a[i][j]=c[i][j];
b[i][j]=0;
}
}
int cnt2=0;
for(int j=1;j<=m;j++)
{
int minn=0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
minn=min(minn,a[i][j]);
}
if(minn==0)continue;
output2+=minn;
ans2[cnt2][0]=1;
ans2[cnt2][1]=j;
ans2[cnt2++][2]=minn;
for(int i=1;i<=n;i++)
{
b[i][j]+=minn;
a[i][j]-=minn;
}
}
for(int i=1;i<=n;i++)
{
int minn=0x3f3f3f3f;
for(int j=1;j<=m;j++)
{
minn=min(minn,a[i][j]);
}
if(minn==0)continue;
output2+=minn;
ans2[cnt2][0]=0;
ans2[cnt2][1]=i;
ans2[cnt2++][2]=minn;
for(int j=1;j<=m;j++)
{
b[i][j]+=minn;
a[i][j]-=minn;
}
}
if(output<=output2)
{
printf("%d\n",output);
for(int i=0;i<cnt;i++)
{
for(int j=0;j<ans[i][2];j++)
{
if(ans[i][0]==0)printf("row ");
else printf("col ");
printf("%d\n",ans[i][1]);
}
}
}
else
{
printf("%d\n",output2);
for(int i=0;i<cnt2;i++)
{
for(int j=0;j<ans2[i][2];j++)
{
if(ans2[i][0]==0)printf("row ");
else printf("col ");
printf("%d\n",ans2[i][1]);
}
}
}
}
else printf("-1\n");
}
}







 本文介绍了一种解决游戏谜题的方法,通过选择行或列加1的方式将初始的0矩阵转换为目标矩阵,旨在使用最少的操作次数完成游戏挑战。
本文介绍了一种解决游戏谜题的方法,通过选择行或列加1的方式将初始的0矩阵转换为目标矩阵,旨在使用最少的操作次数完成游戏挑战。
















 1038
1038

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








