ZZULIOJ 1726 迷宫【状压Bfs+巨多的坑】

最新推荐文章于 2023-06-19 23:01:37 发布

原创最新推荐文章于 2023-06-19 23:01:37 发布 · 375 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#ZZULIOJ 1726

搜索专栏收录该内容

224 篇文章

订阅专栏

本文介绍了一种解决迷宫问题的算法，通过BFS搜索策略找到触发所有机关并离开迷宫所需的最少步数。该算法适用于RPG游戏中的迷宫挑战，能够有效减少玩家尝试不同路径的时间。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1726: 迷宫

Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 536 Solved: 86

Submit Status Web Board

Description

在很多 RPG (Role-playing Games) 游戏中，迷宫往往是非常复杂的游戏环节。通常来说，我们在走迷宫的时候都需要花非常多的时间来尝试不同的路径。但如果有了算法和计算机的帮助，我们能不能有更快的方式来解决这个问题？我们可以进行一些尝试。
现在我们有一个 N 行 M 列的迷宫。迷宫的每个格子如果是空地则可以站人，如果是障碍则不行。在一个格子上，我们可以一步移动到它相邻的 8 个空地上，但不能离开地图的边界或者跨过两个障碍的夹缝。下图是一个移动规则的示例。
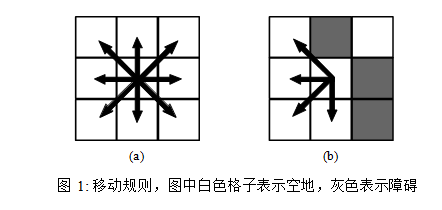
为了离开迷宫，我们还需要触发迷宫中所有的机关。迷宫里总共有 K 个机关，每个机关都落在一个不同的空地上。如果我们到达了某个机关所在的格子时，这个机关就会被自动触发，并在触发之后立即消失。我们的目标是按顺序触发所有的 K             个机关，而当最后一个机关被触发时，我们就可以离开迷宫了。
现在我们已经拿到了迷宫地图，并且知道所有障碍、机关的位置。初始时我们位于迷宫的某个非障碍格子上，请你计算我们最少需要移动多少步才能离开迷宫？

Input

输入的第一行是测试数据的组数 T (T ≤ 20)。
对于每组测试数据：第一行包含地图的行数 N (2 ≤ N  ≤ 100)，列数 M(2 ≤ M  ≤ 100) 和机关的数量 K(1 ≤ K ≤10)。接下来 N 行，每行包含 M 个字符，其中字符 ‘#’ 表示障碍，而 ‘.’ 表示空地。接下来一行描述了我们的初始位置 (x, y)，表示我们一开始在第 x 行第 y 列的格子上。这个格子保证是个空地。接下来 K 行，每行给出了一个机关的位置。所有的机关都不会出现在障碍上，并且任意两个机关不会出现在同一个空地上。我们需要按输入给定的顺序触发所有的 K 个机关。

Output

对于每组测试数据，输出离开迷宫所需要的最少步数。如果无论如何都不能离开迷宫，输出 -1。

Sample Input

3

 
 3 3 2

...

...

...

1 1

1 3

2 2

 
 3 3 1

...

.#.

...

1 1

3 3

 
 2 3 1

 
 ..
 #

 
 .
 #.

1 1

2 3

Sample Output

3

3

-1

思路：

1、一共只有十个机关，那么对应我们设定vis【i】【j】【k】表示到位子（i，j），已经走过了状态为k的机关的最小步数。

那么对应过程Bfs即可。

2、这类题主要就是坑点比较恶心：

①起点可能有机关，而且如果起点的机关不是第一个机关。这样结果一定是-1.

②走到过的机关一踩就没，所以如果我们没有走到过机关2，那么一定不能先经过机关3 ，这样就GG了。

提供数据：

3 3 2

.#.

...

1 1

1 3

2 2

ans:5

wrong ans:3

③注意实现细节，比如位运算的括号，别的就没什么了，代码实现很简单。

Ac代码：

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<queue>
using namespace std;
struct node
{
    int x,y,step,tmp;
}now,nex;
int n,m,kk;
char a[102][102];
int fx[8]={1,-1,0,0,1,-1,1,-1};
int fy[8]={0,0,1,-1,1,-1,-1,1};
int vis[102][102][1028];
void Bfs(int sx,int sy)
{
    memset(vis,0,sizeof(vis));
    int end=(1<<kk)-1;
    now.x=sx;
    now.y=sy;
    now.step=0;
    if(a[now.x][now.y]=='0')
    {
        now.tmp=1;
    }
    else if(a[now.x][now.y]>='1'&&a[now.x][now.y]<='9')
    {
        printf("-1\n");
        return ;
    }
    else now.tmp=0;
    vis[now.x][now.y][now.tmp]=1;
    queue<node >s;
    s.push(now);
    while(!s.empty())
    {
        now=s.front();
      //  printf("%d %d %d step:--%d\n",now.x,now.y,now.tmp,now.step);
        if(now.tmp==end)
        {
            printf("%d\n",now.step);
            return ;
        }
        s.pop();
        for(int i=0;i<4;i++)
        {
            nex.x=now.x+fx[i];
            nex.y=now.y+fy[i];
            nex.step=now.step+1;
            if(nex.x>=0&&nex.x<n&&nex.y>=0&&nex.y<m&&a[nex.x][nex.y]!='#')
            {
                if(a[nex.x][nex.y]=='.')
                {
                    nex.tmp=now.tmp;
                }
                else
                {
                    int zz=a[nex.x][nex.y]-'0';
                    zz=(1<<zz);
                    if(zz==1||(((now.tmp*2)&zz)>0))
                    {
                        if((now.tmp&zz)==0)
                        {
                            nex.tmp=now.tmp+zz;
                        }
                        else nex.tmp=now.tmp;
                    }
                    else continue;
                }
                if(vis[nex.x][nex.y][nex.tmp]==0)
                {
                    vis[nex.x][nex.y][nex.tmp]=1;
                    s.push(nex);
                }
            }
        }
        for(int i=4;i<8;i++)
        {
            nex.x=now.x+fx[i];
            nex.y=now.y+fy[i];
            nex.step=now.step+1;
            if(nex.x>=0&&nex.x<n&&nex.y>=0&&nex.y<m&&a[nex.x][nex.y]!='#')
            {
                if(a[now.x+fx[i]][now.y]=='#'&&a[now.x][now.y+fy[i]]=='#')continue;
                if(a[nex.x][nex.y]=='.')
                {
                    nex.tmp=now.tmp;
                }
                else
                {
                    int zz=a[nex.x][nex.y]-'0';
                    zz=(1<<zz);
                    if(zz==1||(((now.tmp*2)&zz)>0))
                    {
                        if((now.tmp&zz)==0)
                        {
                            nex.tmp=now.tmp+zz;
                        }
                        else nex.tmp=now.tmp;
                    }
                    else continue;
                }
                if(vis[nex.x][nex.y][nex.tmp]==0)
                {
                    vis[nex.x][nex.y][nex.tmp]=1;
                    s.push(nex);
                }
            }
        }
    }
    printf("-1\n");
    return ;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d",&n,&m,&kk);
        for(int i=0;i<n;i++)scanf("%s",a[i]);
        int sx,sy;
        scanf("%d%d",&sx,&sy);
        int num=0;
        for(int i=0;i<kk;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            x--;y--;
            a[x][y]=num+'0';
            num++;
        }
        Bfs(sx-1,sy-1);
    }
}
/*
3
3 3 2
.#.
...
...
1 1
1 3
2 2
*/