Leet Code 笔记

Leet Code 笔记

53. Maximum Subarray 最大子段和

2019.07.22
leetcode 53

动态规划

原数组$num[]$
记录数组$sum[i]$保存的是原数组以位置$i$结尾在$num[0...i]$区间内的最大子段和
初始值$sum[0]$=$num[0]$
可以写出如下递推公式：

$$sum[i]=\{\begin{array}{ll}sum[i-1]+num[i]& \text{if}sum[i-1]>0\\ num[i]& \text{else}\end{array}$$
因为只需要求得最大的结果，所以可以用一个变量$res$来代替$sum[i-1]$的功能，从前到后扫描一次数组，并用一个变量$maxv$记录最大的$res$返回.

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res = nums[0]
        maxv = nums[0]
        for i in range(1, len(nums)):
            res = res + nums[i] if res > 0 else nums[i]
            if maxv < res:
                maxv = res
        return maxv

---

62. Unique Paths 不同的路径

2019.07.22
leetcode 62

组合数学

这个问题其实可以转化成组合数学。因为每次只能向右或向下走一步，最多能走的是向右$m-1$步，向下$n-1$步。假设$n<m$，其实是在$m-1$步的间隔位置包括开始和结尾，插入$n-1$步，并且可以连续插入在同一个间隔。将向右移视为$1$，向下移视为$0$，问题转化为在$（m+n-2）$个位置上选择$（m-1）$个放置$1$，其余放置$0$，可以直接用组合公式求解。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        return self.cfun(m+n - 2,n - 1)
 
    def cfun(self,a,b):
        min = a-b if a-b < b else b
        res = 1
        for i in range(min):
            res = res *  (a - i) // (i + 1)
        return res

动态规划

---

160. Intersection of Two Linked Lists 两个链表的交汇点

2019.09.06
leetcode 160

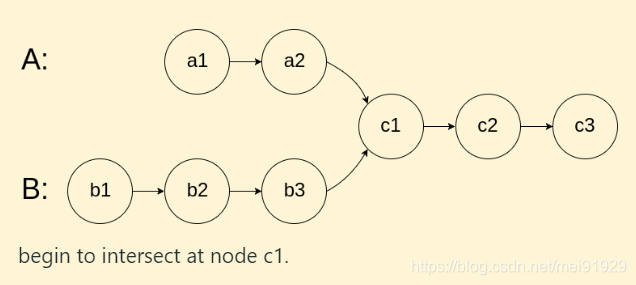
双指针法

1. 可以遍历一遍两个链表，然后让长的链表先出发，到达他们长度相同的位置后，同时出发，当两个指针相等时退出循环
2. 更巧妙地方法是，让两个指针同时出发，当其中一个走到链表尾端，此时它等于$null$，将它置为另一个链表的开头，继续前进，直到两个指针相等时退出循环。具体证明：
   设$A$链表长度为$lenA$，$B$链表长度为$lenB$，
   当其中一个指针走到结尾，将它置为另一个链表的开始，这样他会多走另一个链表的长度，
   $$\text{len}{A}^{\prime }=\text{len}A+\text{len}B$$
   $$\text{len}{B}^{\prime }=\text{len}B+\text{len}A$$
   $$\text{len}{A}^{\prime }=\text{len}{B}^{\prime }$$
   他们走的总长度相同，所以总会在交汇点处相遇。另外，当$c=0$时，他们都为$null$，此时跳出循环并返回$null$。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        //boundary check
        if(headA == null || headB == null) return null;
    
        ListNode a = headA;
        ListNode b = headB;
    
        //if a & b have different len, then we will stop the loop after second iteration
        while( a != b){
    	//for the end of first iteration, we just reset the pointer to the head of another linkedlist
            a = a == null? headB : a.next;
            b = b == null? headA : b.next;    
        }
    
        return a;
    }
}

---

167. Two Sum II 两数之和2

leetcode 167

双指针法

因为是排序好的数组，头尾各一个指针向中间遍历，如果两数之和等于目标值，跳出循环，如果大于则移动尾指针，使和变小，否则移动头指针，使和变大，直到两个指针相遇。

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int[] ans = new int[2];
        int left = 0;
        int right = numbers.length-1;
        while(left != right){
            int sum = numbers[left]   + numbers[right];
            if(sum == target){
                ans[0] = left + 1;
                ans[1]= right + 1;
                break;
            }
            else if(sum > target){
                right--;
            }
            else{
                left++;
            }
        }
        return ans;
    }
}

---

241 加括号的不同结果

leetcode 241

分治算法

原问题可以从运算符号位置拆分为左右各一个子问题，运用递归不断求解子问题，组合成原问题。加速的方法使用备忘录，记录之前计算过的子问题。

public class Solution {
    private HashMap<String, List<Integer>> hashmap = new HashMap<String, List<Integer>>();
    public List<Integer> diffWaysToCompute(String input) {
        if(hashmap.containsKey(input))
            return hashmap.get(input);
        List<Integer> res = new ArrayList<Integer>();
        for(int i = 0; i < input.length(); i++){
            char ch = input.charAt(i);
            if(ch == '*' || ch == '+' || ch == '-')
                for(int l: diffWaysToCompute(input.substring(0, i)))
                    for(int r: diffWaysToCompute(input.substring(i+1)))
                        switch(ch){
                            case '*': res.add(l * r);
                                break;
                            case '+': res.add(l+r);
                                break;
                            case '-': res.add(l-r);
                                break;
                            default: break;
                        }
        }
        if(res.size()==0)
            res.add(Integer.valueOf(input));
        hashmap.put(input, res);
        return res;
    }
}