数据结构---B树和B+树

今天看数据结构关于B树和B+树的那一块，感觉挺难得，所以将看的总结了下来，加深记忆吧。主要参考了严蔚敏的书和王道考研书P233.

B树是一种多路平衡查找树，也叫B-树。主要定义如下

      1.定义任意非叶子结点最多只有M个儿子；且M>2；

       2.根结点的儿子数为[2, M]；

       3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

       4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

       5.非叶子结点的关键字个数=指向儿子的指针个数-1；

       6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

       7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

       8.所有叶子结点位于同一层，且不带任何内容，即为空；

       9.每个飞非叶子节点包含的信息如下（n,P[1],A[1],~~~~P[M-1],A[M-1],P[M]）;n代表关键字的个数

如M=3；

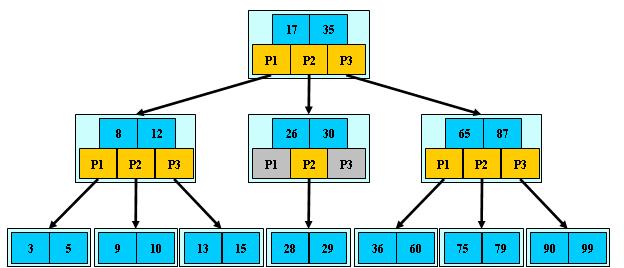
B树的查找

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果

命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为

空，或已经是叶子结点；

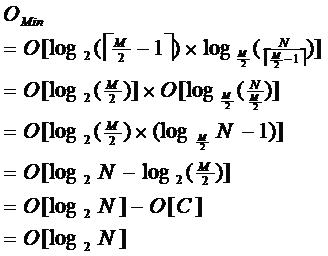
B-树的特性：

1.关键字集合分布在整颗树中；

2.任何一个关键字出现且只出现在一个结点中；

3.搜索有可能在非叶子结点结束；

4.其搜索性能等价于在关键字全集内做一次二分查找；

5.自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少

利用率，其最底搜索性能为：

 

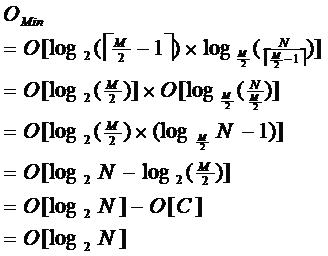
其中，M为设定的非叶子结点最多子树个数，N为关键字总数；

 

 

所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占

M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

B树节点的定义：

typedef struct BTNode
{
      int  keynum;//关键字个数
      struct BTNnode *  parent//指向双亲的节点；
      KeyType   key[m+1];//保存关键字
      struct  BTNode * ptr[m+1];//子树指针
}BTNode,*BTree；

B树查询操作的简单实现

bool   BSearch(BTree T,KeyType  K)
{
     p=T;q=null;found=false;i=0;
     while(p&&!found)
     {
         i=search(p,k);//在p->KEY[]中查找k
         if(i>0&&p->key[i]==K)  return true;//查找成功
         else
         q=p;p=p->ptr[i];
     }

     return found;
}

今天太晚了，明天再写吧······