解题报告 之 HDU5475 An easy problem
Description
One day, a useless calculator was being built by Kuros. Let's assume that number X is showed on the screen of calculator. At first, X = 1. This calculator only supports two types of operation.
1. multiply X with a number.
2. divide X with a number which was multiplied before.
After each operation, please output the number X modulo M.
1. multiply X with a number.
2. divide X with a number which was multiplied before.
After each operation, please output the number X modulo M.
Input
The first line is an integer T(

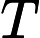


 ),
indicating the number of test cases.
),
indicating the number of test cases.
For each test case, the first line are two integers Q and M. Q is the number of operations and M is described above. (













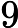 )
)
The next Q lines, each line starts with an integer x indicating the type of operation.
if x is 1, an integer y is given, indicating the number to multiply. (





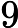 )
)
if x is 2, an integer n is given. The calculator will divide the number which is multiplied in the nth operation. (the nth operation must be a type 1 operation.)
It's guaranteed that in type 2 operation, there won't be two same n.


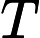


 ),
indicating the number of test cases.
),
indicating the number of test cases. For each test case, the first line are two integers Q and M. Q is the number of operations and M is described above. (














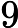 )
) The next Q lines, each line starts with an integer x indicating the type of operation.
if x is 1, an integer y is given, indicating the number to multiply. (






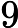 )
) if x is 2, an integer n is given. The calculator will divide the number which is multiplied in the nth operation. (the nth operation must be a type 1 operation.)
It's guaranteed that in type 2 operation, there won't be two same n.
Output
For each test case, the first line, please output "Case #x:" and x is the id of the test cases starting from 1.
Then Q lines follow, each line please output an answer showed by the calculator.
Then Q lines follow, each line please output an answer showed by the calculator.
Sample Input
1 10 1000000000 1 2 2 1 1 2 1 10 2 3 2 4 1 6 1 7 1 12 2 7
Sample Output
Case #1: 2 1 2 20 10 1 6 42 504 84
Source
2015 ACM/ICPC Asia Regional Shanghai Online
题目大意:有一个数X,初始状态为1。给出两种操作,操作1是在现有的数上乘上一个数 y,操作2是除以一个之前已经乘过的某个数。注意操作2绝不会除以一个乘过的数两次。要求每次操作后输出X % M 的值。注意有1e5次操作,0<=y<=1e9。
分析:首先注意题目的描述,只有输出的时候才取模,这里一定要看清楚,不然就是千年WA。很自然的想法是直接硬上,每次都维护一下X的值,不过很容易发现这是不现实的,因为根本存不下那么大的数……然后又会很自然的想到把X表示为乘数 ∏yi
。但是又很明显发现时间复杂度是超过的,因为查询次数1e5。
于是乎必须要有一个log级别的算法。于是乎我组大神机智的想到了线段树(其实我也想到了线段树但是没有理智的分析复杂度。。。)。具体思路是,因为操作数为1e5,那么最多有1e5个乘数,首先假设他们都是1。操作1更新对应的节点为yi,操作2更新对应的节点为1。再由于乘法和取模的可交换性。所以节点的value表示取模后的结果即可。(为什么不用线段树就不能直接存取模后的值,原因在于用了线段树之后,通过将yi变为1后重新乘一次,将除法转为乘法,解决了除法和取模的不可交换性。)
每次操作直接输出root的value即可。还有一个坑点在于叶结点赋值yi时也要取模,血的教训。
上代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
ll tree[maxn * 4];
ll M, X = 1;
void pushUp( int v )
{
tree[v] = tree[v << 1] * tree[(v << 1) + 1] % M;
}
void built( int v, int l, int r )
{
if(l == r)
{
tree[v] = 1;
return;
}
int mid = (l + r) >> 1;
built( v << 1, l, mid );
built( (v << 1) + 1, mid + 1, r );
pushUp( v );
}
void update( int v, int l, int r, int idx, ll val )
{
if(l == r)
{
tree[v] = val%M;
return;
}
int mid = (l + r) >> 1;
if(idx <= mid)
{
update( v << 1, l, mid, idx, val );
}
else
{
update( (v << 1) + 1, mid + 1, r, idx, val );
}
pushUp( v );
}
int main()
{
int T;
cin >> T;
for(int kas = 1; kas <= T; kas++)
{
ll Q;
X = 1;
scanf( "%I64d %I64d", &Q, &M );
printf( "Case #%d:\n", kas );
built( 1, 1, Q );
for(int k = 1; k <= Q; k++)
{
ll opt, ind;
scanf( "%I64d %I64d", &opt, &ind );
if(opt == 1)
{
update( 1, 1, Q, k, ind );
}
if(opt == 2)
{
update( 1, 1, Q, ind, 1 );
}
X = tree[1];
printf( "%I64d\n", X );
}
}
return 0;
}就是这样拉~~膜拜一下新队友叔叔,简直是思维大神,仰视之~







 本文深入解析HDU5475难题,讲解了一个无用计算器的操作规则及其求解策略。面对每种操作类型,包括乘法和除法,并在每次操作后计算并输出结果对M的模。通过引入线段树数据结构优化复杂度,实现高效求解。详细阐述了算法思想与代码实现,旨在帮助读者理解模运算与数据结构在实际问题中的应用。
本文深入解析HDU5475难题,讲解了一个无用计算器的操作规则及其求解策略。面对每种操作类型,包括乘法和除法,并在每次操作后计算并输出结果对M的模。通过引入线段树数据结构优化复杂度,实现高效求解。详细阐述了算法思想与代码实现,旨在帮助读者理解模运算与数据结构在实际问题中的应用。
















 3524
3524


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







