LeetCode【576】 Out of Boundary Paths-优快云博客

本文探讨了一个m×n网格中球从特定起点出发，在限定步数内移动并最终出界的路径数量问题。通过动态规划的方法实现了算法设计，并提供了解决方案的具体代码实现。

There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 109 + 7.
Example 1:
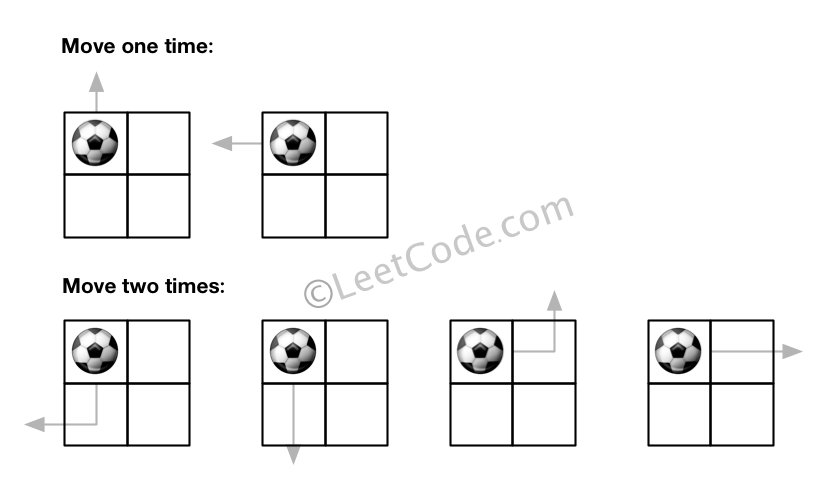
Input:m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation:

Example 2:
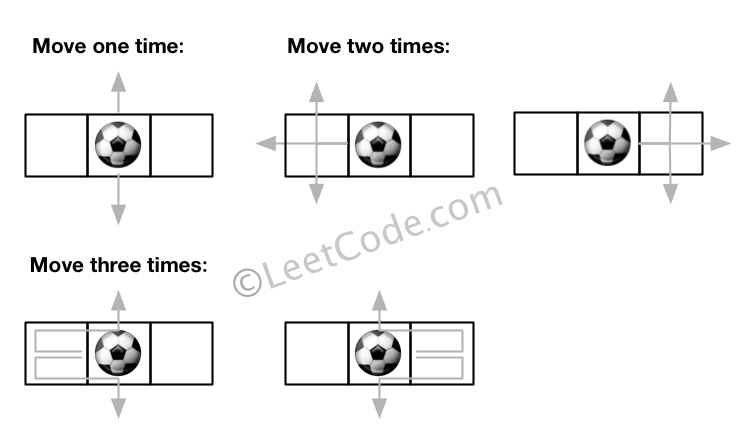
Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation:

本题属于图的问题，我用了动态规划，实现并不很难，不过不太好理解，我是在参考了答案后模仿了别人的算法。

class Solution {
public:
    int findPaths(int m, int n, int N, int i, int j) {
        unsigned int g[50][50] = {}, r[50];
        while (N-- > 0)
        for (auto k = 0; k <= m; ++k)
            for (auto l = 0; l < n; ++l) {
                auto tmp = r[l];
                r[l] = (k == m ? 0 : ((k == 0 ? 1 : g[k - 1][l]) + (k == m - 1 ? 1 : g[k + 1][l])
                    + (l == 0 ? 1 : g[k][l - 1]) + (l == n - 1 ? 1 : g[k][l + 1])) % 1000000007);
                if (k > 0) g[k - 1][l] = tmp;
            }
        return g[i][j];
    }
};