神经网络涉及到的基本概念
- 激活函数
- 损失函数
- 优化器
- 监督学习
感知器
感知器是最简单的神经网络,感知器是对生物的神经元的一种简单模仿,即单经元网络,有输入也有输出。
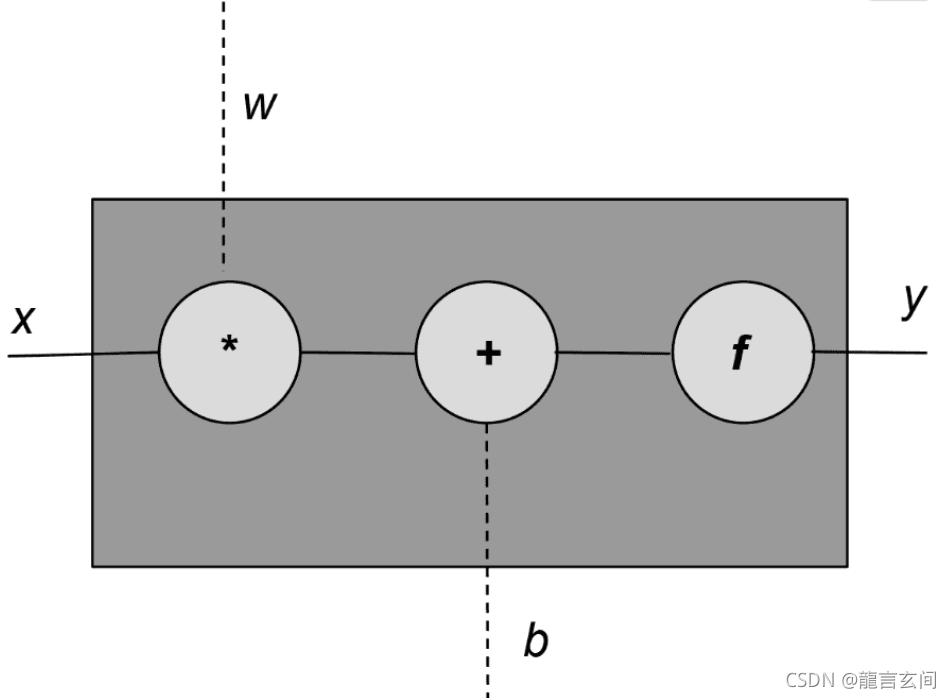
一般来说感知器有多个输入,x和w是向量,x和w的乘积用点积来代替。 每个感知器单元有一个输入(x)和三个旋钮(knobs),一组权重(w),偏量(w)和一个激活函数(f)。
权重和偏差都是从数据里进行学习,激活函数则是基于目标函数和程序员设计的。
感知器表示为 y = f(wx+b)
**通常激活函数f是非线性函数,(wx+b)是显性函数。感知器是线性函数和非线性函数的组合。线性表达式wx+b也被称为放射变换。**应用激活函数并生成单个输出。
PyTorch方便地在torch中提供了一个Linear()类。
激活函数
激活函数是神经网络引入的非线性函数,用于捕获数据里的复杂关系。常用的激活函数有(图片转载自书栈网)
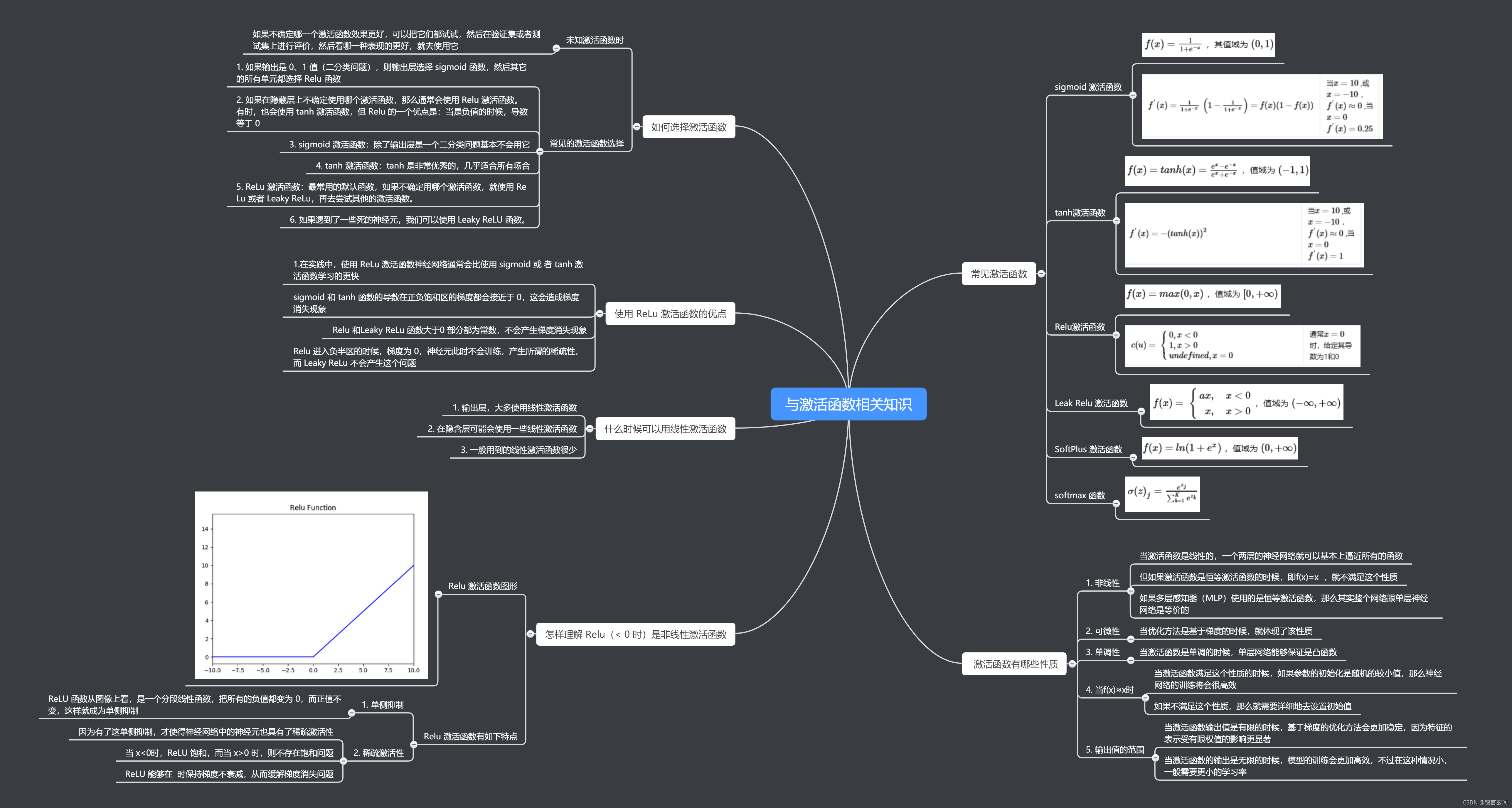
Sigmoid
sigmoid是神经网络历史上最早使用的激活函数之一。它取任何实值并将其压缩在0和1之间。sigmoid是一个光滑可微的函数。
import torch
import matplotlib.pyplot as plt
x = torch.range(-5., 5., 0.1)
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
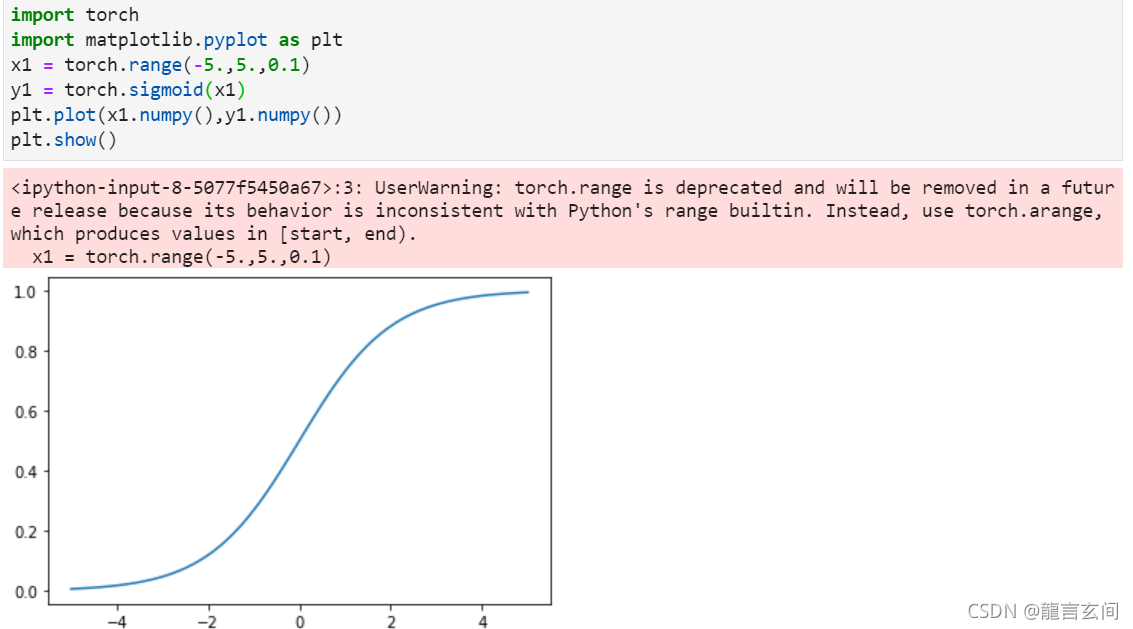
当x1趋近于5的时候,sigmoid函数趋近于饱和且接近最大值。**这可能导致计算梯度为0或者溢出。**这个现象被称为梯度小时或者是梯度爆炸问题。因此,神经网络除了输出端使用sigmoid函数外,其他情况很少使用sigmoid函数,因为在输出端这种挤压的特性可以被解释为概率。
Tanh
tanh激活函数是sigmoid在外观上的不同变体。tanh激活函数和sigmoid函数一样都是挤压函数,它映射一个实值集合从(-∞,+∞)到(-1,+1)范围。
import torch
import matplotlib.pyplot as plt
x2 = torch.range(-10., 10., 0.1)
y2 = torch.tanh(x2)
plt.plot(x2.numpy(), y2.numpy())
plt.show()
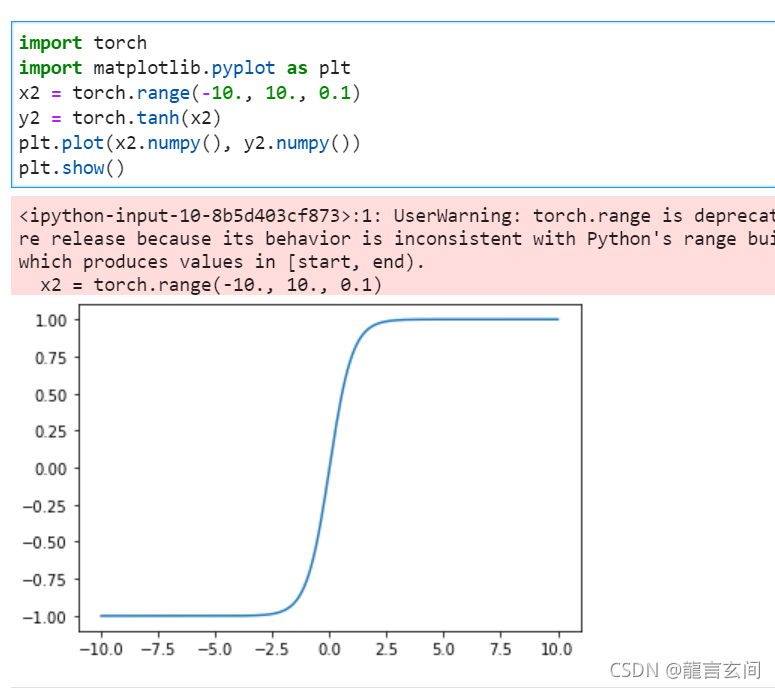
ReLU
ReLU代表线性整流单元。可以说是最重要的激活函数,因为很多深度学习方面的创新是基于此的。函数形式f(x) = max(0,x)。
函数使得负值映射为0,这样可以有助于消除梯度问题。
import torch
import matplotlib.pyplot as plt
relu = torch.nn.ReLU()
x = torch.range(-15., 15., 0.1)
y = relu(x)
plt.plot(x.numpy(), y.numpy())
plt.show()
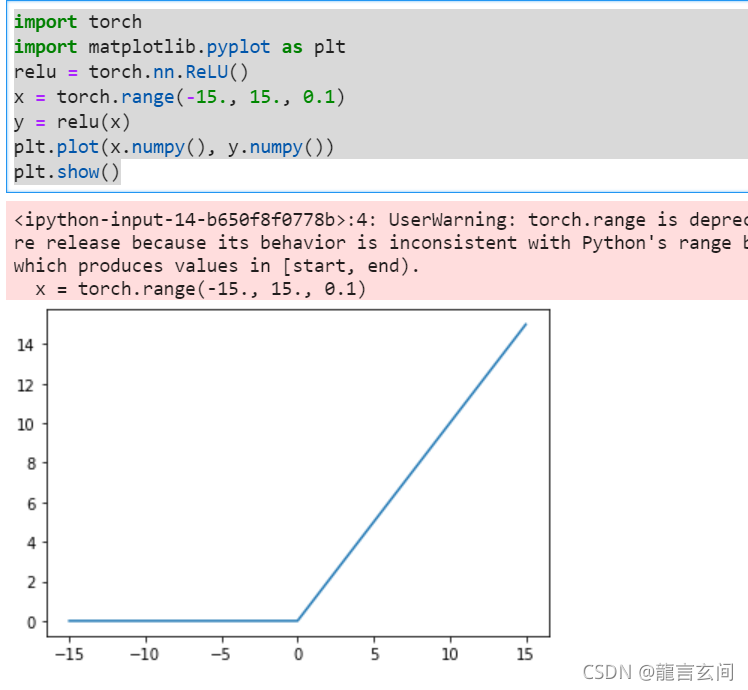
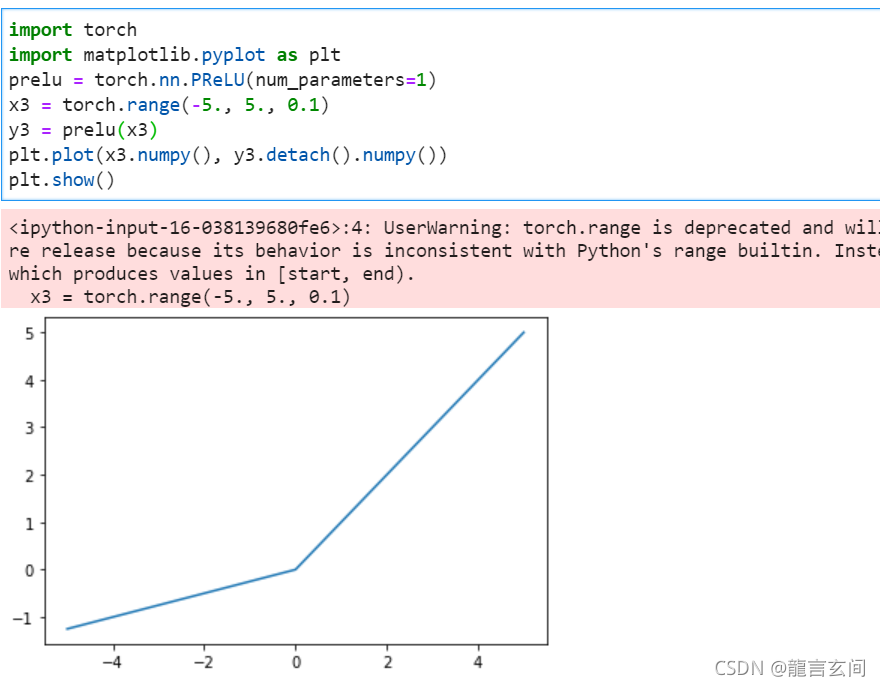
但也可能出现问题,网络里某些输出可能会变为0,再也不会恢复,这是“dying ReLU”问题。基于此问题就提出的函数的变体,比如Leaky ReLU或 Parametric ReLU (PReLU)等relu函数的变体,这两种变体可以统一用以下数学公式来表示: f(x)=max(ax,x)
其中,Leaky ReLU中a固定为0.01,而Parametric ReLU (PReLU)中,a为一个可学习的参数。
import torch
import matplotlib.pyplot as plt
prelu = torch.nn.PReLU(num_parameters=1)
x3 = torch.range(-5., 5., 0.1)
y3 = prelu(x3)
plt.plot(x3.numpy(), y3.detach().numpy())
plt.show()
Softmax
softmax函数类似于sigmoid激活函数,将每个单元的输出都压缩为0到1之间。softmax操作还将输出向量中的每个输出除以所有输出的和,从而得到一个k个类别上离散的概率分布,该概率分布上的所有概率的和为1。Softmax函数数学公式:
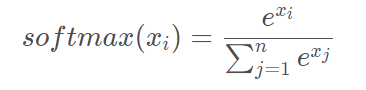
函数的结果的概率之和为1。对于解释分类任务的输出非常有用,因此通常和概率训练目标相匹配,
Input[0]
import torch.nn as nn
import torch
softmax = nn.Softmax(dim=1)
x_input = torch.randn(1, 3)
y_output = softmax(x_input)
print(x_input)
print(y_output)
print(torch.sum(y_output, dim=1))
#tensor([[ 0.5836, -1.3749, -1.1229]])
#tensor([[ 0.7561, 0.1067, 0.1372]])
#tensor([ 1.])
softmax函数现在经常被用作多分类场景中的输出层
损失函数
损失函数的作用,简言之计算模型预测值与实际值之间的残差。损失函数的值越高,模型预测的结果越差。
三个常用的损失函数Mean Squared Error Loss、Categorical Cross-Entropy Loss以及Binary Cross-Entropy。
均方误差损失
Mean Squared Error Loss是均方误差函数,回归问题里网络的输出(ŷ)和目标(y)是连续值,一个常用的损失函数的均方误差(MSE)。
import torch
import torch.nn as nn
mse_loss = nn.MSELoss()
outputs = torch.randn(3, 5, requires_grad=True)
targets = torch.randn(3, 5)
loss = mse_loss(outputs, targets)
print(loss)
#输出 tensor(1.0647, grad_fn=<MseLossBackward>)
MSE是预测值和目标值之差的平方的平均值。其他的几个损失函数也可以用于回归问题,比如平均绝对值(MAE)和均方根误差(RMSE)都是计算输出到目标之间的实值距离。

分类交叉熵损失
分类交叉熵常用于多类分类集,其中输出被解释为类成员概率的预测。目标(y)是n维向量,表示所有类的多项分布。输出的类只有一个是正确的,那这个向量是one hot向量。如果网络输出是n维向量,代表多项分布的预测。
分类交叉熵的表示
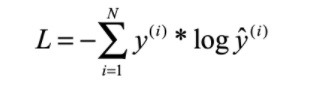
交叉熵起源于信息论,信息论的目的是希望正确类的概率接近1,而其他类的概率接近0。
为了正确地使用PyTorch的交叉熵损失,一定程度上理解网络输出、损失函数的计算方法和来自真正表示浮点数的各种计算约束之间的关系是很重要的。具体来说,有四条信息决定了网络输出和损失函数之间微妙的关系。
- 一个数字的大小是有限制的。
- 如果softmax公式中使用的指数函数的输入是负数,则结果是一个指数小的数,如果是正数,则结果是一个指数大的数。
- 假定网络的输出是应用softmax函数之前的向量。
- 对数函数底数为e时候,是指数函数常数为e的倒函数,和log(exp (x))就等于x
因这四个信息数学简化假设 ,指数函数和log函数是为了更稳定的数值计算和避免很小或很大的数字,使得函数数值更加稳定。
这些简化的结果是,不使用softmax函数的网络输出可以与PyTorch的交叉熵损失一起使用,从而优化概率分布。然后,当网络经过训练后,可以使用softmax函数创建概率分布。
import torch
import torch.nn as nn
ce_loss = nn.CrossEntropyLoss()
outputs = torch.randn(3, 5, requires_grad=True)
#设置一个随机向量模拟网络输出
targets = torch.tensor([1, 0, 3], dtype=torch.int64)
#CrossEntropyLoss()函数假定每个输入都有一个特定的类,并且每个类都是唯一的索引,因此targets有三个元素,一个戴白哦输入正确的类的索引。
loss1 = ce_loss(outputs, targets)
print(loss1)
# tensor(2.1578, grad_fn=<NllLossBackward>)
监督学习
有监督学习需要以下内容:模型、损失函数、训练数据和优化算法。监督学习的训练数据是观察和目标对,模型从观察中计算预测,损失衡量预测相对于目标的误差。训练的目的是利用基于梯度的优化算法来调整模型的参数,使损失尽可能小。
监督学习的核心
示例:使用“玩具”任务的合成数据——将二维点分类
在有监督学习中应选择三个重要组件:模型、损失函数和优化算法。
模型是在本章开头介绍的:感知器。感知器是灵活的,因为它允许任何大小的输入。在典型的建模情况下,输入大小由任务和数据决定。在这个玩具示例中,输入大小为2,因为我们显式地将数据构造为二维平面。
在模型输出为概率的情况下,最合适的损失函数是基于熵的交叉损失。
在这个简化的监督训练示例中,最后的选择点是优化器。当模型产生预测,损失函数测量预测和目标之间的误差时,优化器使用错误信号更新模型的权重。最简单的形式是,有一个超参数控制优化器的更新行为。这个超参数称为学习率,它控制错误信号对更新权重的影响。
#Adam优化器实例
import torch.nn as nn
import torch.optim as optim
input_dim = 2
lr = 0.001
perceptron = Perceptron(input_dim=input_dim)
bce_loss = nn.BCELoss()
optimizer = optim.Adam(params=perceptron.parameters(), lr=lr)
梯度步进(gradient-steeping)算法
- 首先,使用名为zero_grad()的函数清除当前存储在模型(感知器)对象中的所有记帐信息,例如梯度。
- 然后,模型计算给定输入数据(x_data)的输出(y_pred)。
- 接下来,通过比较模型输出(y_pred)和预期目标(y_target)来计算损失。这正是有监督训练信号的有监督部分。PyTorch损失对象(criteria)具有一个名为bcakward()的函数,该函数迭代地通过计算图向后传播损失,并将其梯度通知每个参数。
- 最后,优化器(opt)用一个名为step()的函数指示参数如何在知道梯度的情况下更新它们的值。
基于感知机和二分类的监督学习训练循环
整个训练数据集被划分成多个批(batch)。在文献和本书中,术语minibatch也可以互换使用,而不是“batch”来强调每个batch都明显小于训练数据的大小;例如,训练数据可能有数百万个,而小批数据可能只有几百个。梯度步骤的每一次迭代都在一批数据上执行。
名为batch_size的超参数指定批次的大小。由于训练数据集是固定的,增加批大小会减少批的数量。在多个批处理(通常是有限大小数据集中的批处理数量)之后,训练循环完成了一个epoch。 epoch是一个完整的训练迭代。如果每个epoch的批数量与数据集中的批数量相同,那么epoch就是对数据集的完整迭代。模型是为一定数量的epoch而训练的。
#基于感知机和二分类的监督学习训练循环
for epoch_i in range(n_batches):
#step0:get the data
x_data,y_target = get_toy_data(batch_size)#获取toy数据集
#step1:clear the gradients
perceptron.zero_grad()
#step2:compute the forward pass of model
y_pred = perceptron(x_data,apply_sigmoid = True)
#step3: compute the loss value that we wish to optimize
loss = bce_loss(y_pred,y_target)
#step4:propagate the loss signal backward
loss.backward()
#step5:trigger the optimizer to perform one update
optimizer.step()
正确度量模型的性能
评估指标
核心监督训练循环之外最重要的部分是使用模型从未训练过的数据来客观衡量性能。模型使用一个或多个评估指标进行评估。
准确性是一个常见指标,指训练过程中未见的数据集上预测正确的部分。
分割数据集
最终的目标是很好地概括数据的真实分布
假设我们能够看到无限数量的数据(“真实/不可见的分布”),那么存在一个全局的数据分布。显然,我们不能那样做。相反,我们用有限的样本作为训练数据。我们观察有限样本中的数据分布这是真实分布的近似或不完全图像。如果一个模型不仅减少了训练数据中样本的误差,而且减少了来自不可见分布的样本的误差,那么这个模型就比另一个模型具有更好的通用性。当模型致力于降低它在训练数据上的损失时,它可以过度适应并适应那些实际上不是真实数据分布一部分的特性。
为实现概括数据的真实分布的目标有两个主要方式,
- 对于数据集分割为三个随机采样的分区,训练、验证和测试数据集,一个常见的分割百分比是预留70%用于训练,15%用于验证,15%用于测试。不过,这不是一个硬性的约定。
- 进行k-fold交叉验证。将整个数据集分割为k个大小相同的fold。其中一个fold保留用于评估,剩下的k-1fold用于训练。通过交换出计算中的fold,可以重复执行此操作。因为有k个fold,每一个fold都有机会成为一个评价fold,并产生一个特定于fold的精度,从而产生k个精度值。最终报告的准确性只是具有标准差的平均值。
知道何时停止训练
最简单的办法就是针对固定数量的周期进行模型训练,但是这个方式过于随意且无必要。
常见的方法是“启发式方法”,工作原理是跟踪验证数据集上的性能,并注意何时不在提高性能。如果性能没有继续得到改善,训练终止。
结束训练前epoch的数量被称为容忍性,一般情况下模型停止对某些数据集进行改进的点成为模型的收敛点。
找到何时超参数
超参数影响模型里参数数量和参数取值的任意模型设置,如损失函数、优化算法、学习率、层的大小、启发式学习的容忍性等等。
正则化
在训练数据不够多时,或者overtraining时,常常会导致过拟合(overfitting)。正则化方法即为在此时向原始模型引入额外信息,以便防止过拟合和提高模型泛化性能的一类方法的统称。在实际的深度学习场景中我们几乎总是会发现,最好的拟合模型(从最小化泛化误差的意义上)是一个适当正则化的大型模型。
- 参数范数惩罚
通过向目标函数添加一个参数范数惩罚Ω(θ)项来降低模型的容量,是一类常用的正则化方法。将正则化后的损失函数记作 :
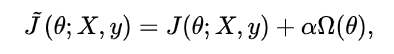
- L2正则化
L2参数正则化通过向目标函数添加一个正则项Ω(θ) = (|w|*|w)|/2 ,使权重更加接近原点。L2参数正则化方法也叫做权重衰减,有时候也叫做岭回归(ridge regression)。正则化的损失函数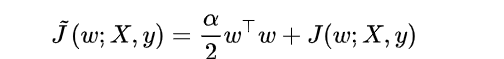
- L1正则化
对模型参数 的L1正则化被定义为:Ω(θ) = ||W|| = ∑ |W|i ,即各个参数的绝对值之和。正则化的损失函数
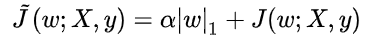





 本文介绍了神经网络的基本概念,包括感知器、激活函数、损失函数及优化器等。详细讲解了Sigmoid、ReLU等激活函数的特点与应用场景,以及MSE、交叉熵等损失函数的计算方法。
本文介绍了神经网络的基本概念,包括感知器、激活函数、损失函数及优化器等。详细讲解了Sigmoid、ReLU等激活函数的特点与应用场景,以及MSE、交叉熵等损失函数的计算方法。
















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








