【智能优化算法】OOBO：一种解决优化问题的新元启发式算法附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

🔥 内容介绍

在当今竞争激烈的商业环境中，企业需要不断寻求提高效率和优化业务流程的方法。而一对一基于优化器正是一种能够帮助企业实现这一目标的工具。本文将探讨一对一基于优化器的概念、优势和应用。

一对一基于优化器是一种基于个体需求和特征的优化方法。它通过对每个个体的特征和需求进行分析，从而设计出最优化的解决方案。与传统的批量处理方法不同，一对一基于优化器更加个性化和精细化，能够更好地满足客户的需求。

一对一基于优化器的优势在于其个性化和精细化的特点。通过对每个个体的需求进行深入分析，企业可以为客户提供更加个性化的产品和服务，从而提高客户满意度和忠诚度。此外，一对一基于优化器还能够帮助企业提高运营效率，降低成本，提高竞争力。

一对一基于优化器的应用非常广泛。在零售行业，企业可以通过分析每个客户的购买历史和偏好，为其推荐个性化的产品和促销活动。在制造业，企业可以根据每个客户的需求定制产品，提高客户满意度。在金融行业，企业可以通过分析每个客户的风险偏好和投资目标，为其提供个性化的投资建议。

然而，一对一基于优化器也面临一些挑战。首先，个性化和精细化需要大量的数据支持，因此企业需要投入大量的时间和资源来收集和分析数据。其次，个性化和精细化也需要企业具有高度的灵活性和响应速度，以便及时调整解决方案。

总的来说，一对一基于优化器是一种能够帮助企业提高效率和优化业务流程的重要工具。通过个性化和精细化的方法，企业可以更好地满足客户的需求，提高客户满意度和忠诚度。然而，企业在应用一对一基于优化器时也需要面对一些挑战，需要克服数据收集和分析的困难，以及提高灵活性和响应速度。只有充分认识到这些挑战，企业才能更好地利用一对一基于优化器，实现持续的竞争优势。

📣 部分代码

function [lb,ub,dim,fobj] = Get_Functions_details(F)​​switch F    case 'F1'        fobj = @F1;        lb=-100;        ub=100;        dim=10;            case 'F2'        fobj = @F2;        lb=-10;        ub=10;        dim=10;            case 'F3'        fobj = @F3;        lb=-100;        ub=100;        dim=30;            case 'F4'        fobj = @F4;        lb=-10;        ub=10;        dim=30;            case 'F5'        fobj = @F5;        lb=-30;        ub=30;        dim=30;            case 'F6'        fobj = @F6;        lb=-100;        ub=100;        dim=30;            case 'F7'        fobj = @F7;        lb=-1.28;        ub=1.28;        dim=30;            case 'F8'        fobj = @F8;        lb=-10;        ub=10;        dim=10;            case 'F9'        fobj = @F9;        lb=-10;        ub=10;        dim=10;​    case 'F10'        fobj = @F10;        lb=-1;        ub=1;        dim=30;            case 'F11'        fobj = @F11;        lb=-100;        ub=100;        dim=30;            case 'F12'        fobj = @F12;        lb=-10;        ub=10;        dim=10;            case 'F13'        fobj = @F13;        lb=-500;        ub=500;        dim=30;            case 'F14'        fobj = @F14;        lb=-5.12;        ub=5.12;        dim=10;            case 'F15'        fobj = @F15;        lb=-32;        ub=32;        dim=10;            case 'F16'        fobj = @F16;        lb=-600;        ub=600;        dim=10;            case 'F17'        fobj = @F17;        lb=-50;        ub=50;        dim=30;            case 'F18'        fobj = @F18;        lb=-50;        ub=50;        dim=30;            case 'F19'        fobj = @F19;        lb=-500;        ub=500;        dim=30;            case 'F20'        fobj = @F20;        lb=-5;        ub=5;        dim=4;                 case 'F21'        fobj = @F21;        lb=-5.12;        ub=5.12;        dim=2;                case 'F22'        fobj = @F22;        lb=-10;        ub=10;        dim=2;                      case 'F23'        fobj = @F23;        lb=-100;        ub=100;        dim=2;             case 'F24'        fobj = @F24;        lb=-65.536;        ub=65.536;        dim=2;            case 'F25'        fobj = @F25;        lb=-5;        ub=5;        dim=4;            case 'F26'        fobj = @F26;        lb=-5;        ub=5;        dim=2;            case 'F27'        fobj = @F27;        lb=[-5,0];        ub=[10,15];        dim=2;            case 'F28'        fobj = @F28;        lb=-2;        ub=2;        dim=2;            case 'F29'        fobj = @F29;        lb=0;        ub=1;        dim=3;            case 'F30'        fobj = @F30;        lb=0;        ub=1;        dim=6;                 case 'F31'        fobj = @F31;        lb=0;        ub=10;        dim=4;                case 'F32'        fobj = @F32;        lb=0;        ub=10;        dim=4;                case 'F33'        fobj = @F33;        lb=0;        ub=10;        dim=4;                   case 'F34'        fobj = @F34;        lb=-100;        ub=100;        dim=2;            case 'F35'        fobj = @F35;        lb=-4;        ub=5;        dim=30;end​end​% F1​function o = F1(x)o=sum(x.^2);end​% F2​function o = F2(x)o=sum(abs(x))+prod(abs(x));% o = ((sin(sqrt(sum(x.^2))))^2-0.5)/(1+0.001*sum(x.^2))+0.5;end​% F3​function o = F3(x)dim=size(x,2);o=0;for i=1:dim    o=o+sum(x(1:i))^2;endend​% F4​function o = F4(x)o=max(abs(x));end​% F5​function o = F5(x)dim=size(x,2);o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);end​% F6​function o = F6(x)o=sum(abs((x+.5)).^2);end​% F7​function o = F7(x)dim=size(x,2);o=sum([1:dim].*(x.^4))+rand;end​% F8​function o = F8(x)dim = size(x, 2);o = sum([1:dim].*(x.^2));end​% F9​function o = F9(x)o=sum(abs(x.*sin(x)+0.1*x));end​% F10​function o = F10(x)dim = size(x, 2);o = 0;for i = 1:dim    o = o+abs(x(i))^(i+1);endend​% F11​function o = F11(x)dim=size(x,2);o = 0;for i = 1:dim    o = o+(10^6)^((i-1)/(dim-1))*x(i)^2;endend​% F12​function o = F12(x)dim = size(x, 2);p = 0; o = sum(x.^2);for i = 1:dim    p = p+0.5*i*x(i);endo = o+p^2+p^4;end​​% F13​function o = F13(x)o=sum(-x.*sin(sqrt(abs(x))));end​% F14​function o = F14(x)dim=size(x,2);o=sum(x.^2-10*cos(2*pi.*x))+10*dim;end​% F15​function o = F15(x)dim=size(x,2);o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);end​% F16​function o = F16(x)dim=size(x,2);o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;end​% F17​function o = F17(x)dim=size(x,2);o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));end​% F18​function o = F18(x)dim=size(x,2);o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));end​% F19​function o = F19(x)o = 418.9829*size(x, 2)-sum(x.*sin(sqrt(abs(x))));end​% F20​function o = F20(x)aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);end​% F21​function o = F21(x)o = -(1+cos(12*sqrt(x(1)^2+x(2)^2)))/(0.5*(x(1)^2+x(2)^2)+2);end​% F22​function o = F22(x)o = 0.26*(x(1)^2+x(2)^2)-0.48*x(1)*x(2);end​% F23​function o = F23(x)o = 0.5+((sin(sqrt(x(1)^2+x(2)^2))^2)-0.5)/(1+0.001*(x(1)^2+x(2)^2)^2);end% F24​function o = F24(x)aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];​for j=1:25    bS(j)=sum((x'-aS(:,j)).^6);endo=(1/500+sum(1./([1:25]+bS))).^(-1);end​% F25​function o = F25(x)aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);end​% F26​function o = F26(x)o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);end​% F27​function o = F27(x)o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;end​% F28​function o = F28(x)o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...    (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));end​% F29​function o = F29(x)aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];o=0;for i=1:4    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend​% F30​function o = F30(x)aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];cH=[1 1.2 3 3.2];pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;....2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];o=0;for i=1:4    o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend​% F31​function o = F31(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];​o=0;for i=1:5    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend​% F32​function o = F32(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];​o=0;for i=1:7    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend​% F33​function o = F33(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];​o=0;for i=1:10    o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend​% F34​function o = F34(x)o = x(1)^2+2*x(2)^2-0.3*cos(3*pi*x(1))-0.4*cos(4*pi*x(2))+0.7;end​% F35​function o = F35(x)o = 0;for i = 1:floor(size(x, 2)/4)    o = o+(x(4*i-3)+10*x(4*i-2))^2+5*(x(4*i-1)-x(4*i))^2+(x(4*i-2)-2*x(4*i-1))^4+10*(x(4*i-3)-x(4*i))^4;endend​function o=Ufun(x,a,k,m)o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));end

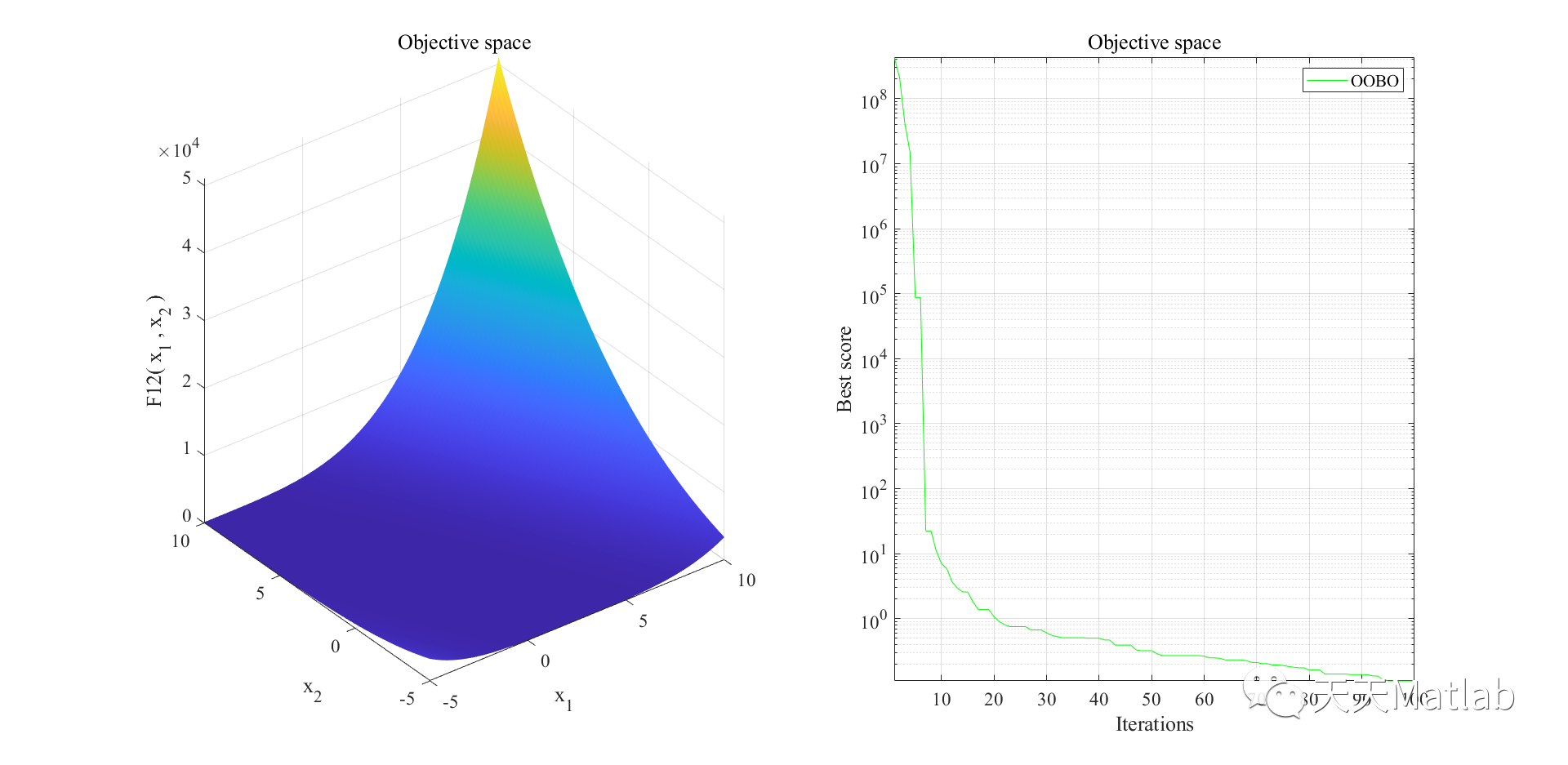
⛳️ 运行结果

🔗 参考文献

本程序参考以下中文EI期刊，程序注释清晰，干货满满。

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合