✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,
代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
信号去噪一直是数字信号处理领域的一个重要研究方向。在实际应用中,由于信号受到各种干扰和噪声的影响,需要对信号进行去噪处理,以提高信号的质量和可靠性。本文将介绍一种基于融合正余弦和柯西变异麻雀算法优化变分模态分解SCSSA-VMD实现信号去噪的算法流程。
首先,介绍一下SCSSA-VMD算法。SCSSA-VMD是一种基于变分模态分解(VMD)的信号去噪算法,它可以将信号分解成一系列固有模态函数(IMF)。这些IMF是不同频率的信号成分,可以通过对这些IMF进行加权和来重建原始信号。SCSSA-VMD算法在VMD分解过程中加入了正余弦函数的约束,以增强分解的稳定性和准确性。
然后,介绍一下柯西变异麻雀算法。柯西变异麻雀算法是一种优化算法,它基于柯西分布和变异策略,通过对候选解进行随机变异和选择,来搜索最优解。柯西分布具有长尾特性,可以避免算法陷入局部最优解。变异策略可以保证算法的全局搜索能力。
接下来,介绍一下融合正余弦和柯西变异麻雀算法优化SCSSA-VMD的算法流程。首先,将待处理的信号进行SCSSA-VMD分解,得到一系列IMF。然后,将正余弦函数加入到VMD分解过程中,得到正余弦约束下的IMF。接着,将柯西变异麻雀算法应用于IMF的加权和,以优化重建信号的质量和可靠性。最后,通过对优化后的IMF进行加权和,得到去噪后的信号。
总的来说,融合正余弦和柯西变异麻雀算法优化SCSSA-VMD是一种有效的信号去噪算法。它不仅可以提高信号的质量和可靠性,还可以保证算法的全局搜索能力和稳定性。在实际应用中,可以根据具体情况选择不同的参数和算法流程,以达到最佳效果。
📣 部分代码
function [u, u_hat, omega] = VMD(signal, alpha, tau, K, DC, init, tol)%%% Input and Parameters:% ---------------------% signal - the time domain signal (1D) to be decomposed% alpha - the balancing parameter of the data-fidelity constraint% tau - time-step of the dual ascent ( pick 0 for noise-slack )% K - the number of modes to be recovered% DC - true if the first mode is put and kept at DC (0-freq)% init - 0 = all omegas start at 0% 1 = all omegas start uniformly distributed% 2 = all omegas initialized randomly% tol - tolerance of convergence criterion; typically around 1e-6%% Output:% -------% u - the collection of decomposed modes% u_hat - spectra of the modes% omega - estimated mode center-frequencies%---------- Preparations% Period and sampling frequency of input signalsave_T = length(signal);fs = 1/save_T;% extend the signal by mirroringT = save_T;f_mirror(1:T/2) = signal(T/2:-1:1);f_mirror(T/2+1:3*T/2) = signal;f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);f = f_mirror;% Time Domain 0 to T (of mirrored signal)T = length(f);t = (1:T)/T;% Spectral Domain discretizationfreqs = t-0.5-1/T;% Maximum number of iterations (if not converged yet, then it won't anyway)N = 500;% For future generalizations: individual alpha for each modeAlpha = alpha*ones(1,K);% Construct and center f_hatf_hat = fftshift((fft(f)));f_hat_plus = f_hat;f_hat_plus(1:T/2) = 0;% matrix keeping track of every iterant // could be discarded for memu_hat_plus = zeros(N, length(freqs), K);% Initialization of omega_komega_plus = zeros(N, K);switch initcase 1for i = 1:Komega_plus(1,i) = (0.5/K)*(i-1);endcase 2omega_plus(1,:) = sort(exp(log(fs) + (log(0.5)-log(fs))*rand(1,K)));otherwiseomega_plus(1,:) = 0;end% if DC mode imposed, set its omega to 0if DComega_plus(1,1) = 0;end% start with empty dual variableslambda_hat = zeros(N, length(freqs));% other initsuDiff = tol+eps; % update stepn = 1; % loop countersum_uk = 0; % accumulator% ----------- Main loop for iterative updateswhile ( uDiff > tol && n < N ) % not converged and below iterations limit% update first mode accumulatork = 1;sum_uk = u_hat_plus(n,:,K) + sum_uk - u_hat_plus(n,:,1);% update spectrum of first mode through Wiener filter of residualsu_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);% update first omega if not held at 0if ~DComega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);end% update of any other modefor k=2:K% accumulatorsum_uk = u_hat_plus(n+1,:,k-1) + sum_uk - u_hat_plus(n,:,k);% mode spectrumu_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);% center frequenciesomega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);end% Dual ascentlambda_hat(n+1,:) = lambda_hat(n,:) + tau*(sum(u_hat_plus(n+1,:,:),3) - f_hat_plus);% loop countern = n+1;% converged yet?uDiff = eps;for i=1:KuDiff = uDiff + 1/T*(u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i))*conj((u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i)))';enduDiff = abs(uDiff);end%------ Postprocessing and cleanup% discard empty space if converged earlyN = min(N,n);omega = omega_plus(1:N,:);% Signal reconstructionu_hat = zeros(T, K);u_hat((T/2+1):T,:) = squeeze(u_hat_plus(N,(T/2+1):T,:));u_hat((T/2+1):-1:2,:) = squeeze(conj(u_hat_plus(N,(T/2+1):T,:)));u_hat(1,:) = conj(u_hat(end,:));u = zeros(K,length(t));for k = 1:Ku(k,:)=real(ifft(ifftshift(u_hat(:,k))));end% remove mirror partu = u(:,T/4+1:3*T/4);% recompute spectrumclear u_hat;for k = 1:Ku_hat(:,k)=fftshift(fft(u(k,:)))';endend
⛳️ 运行结果
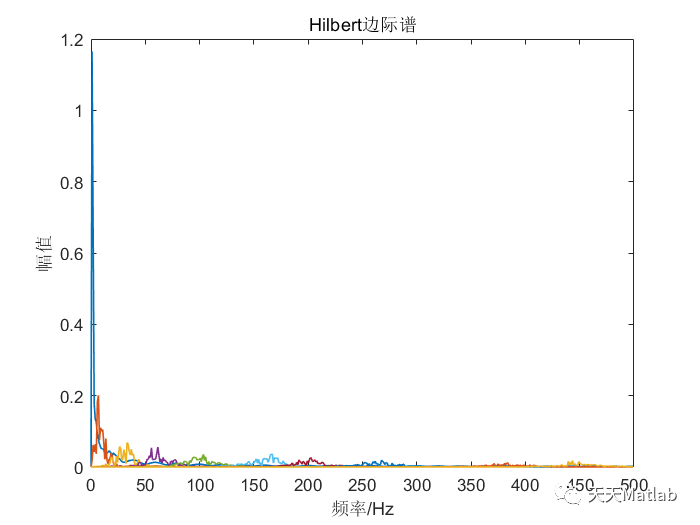
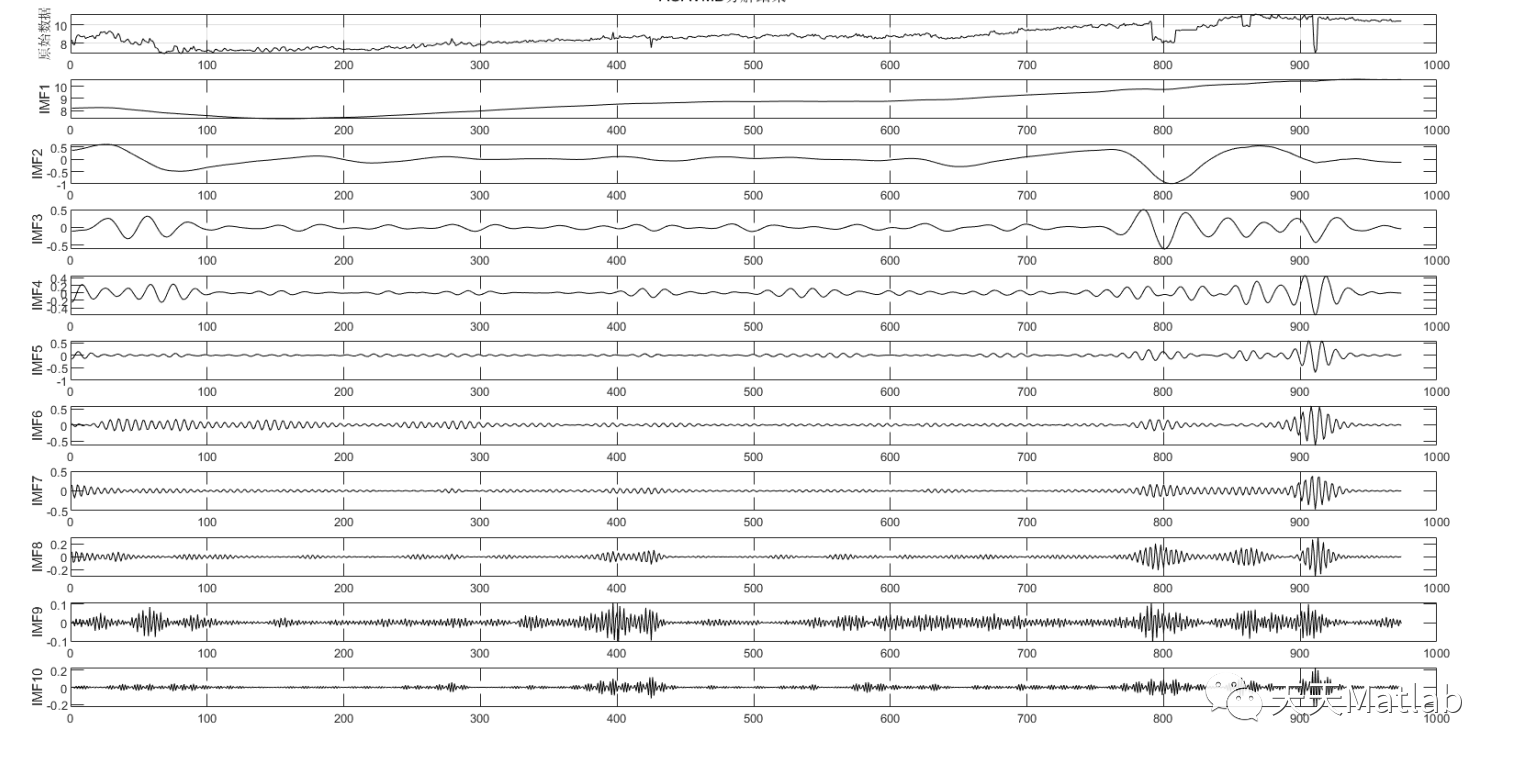
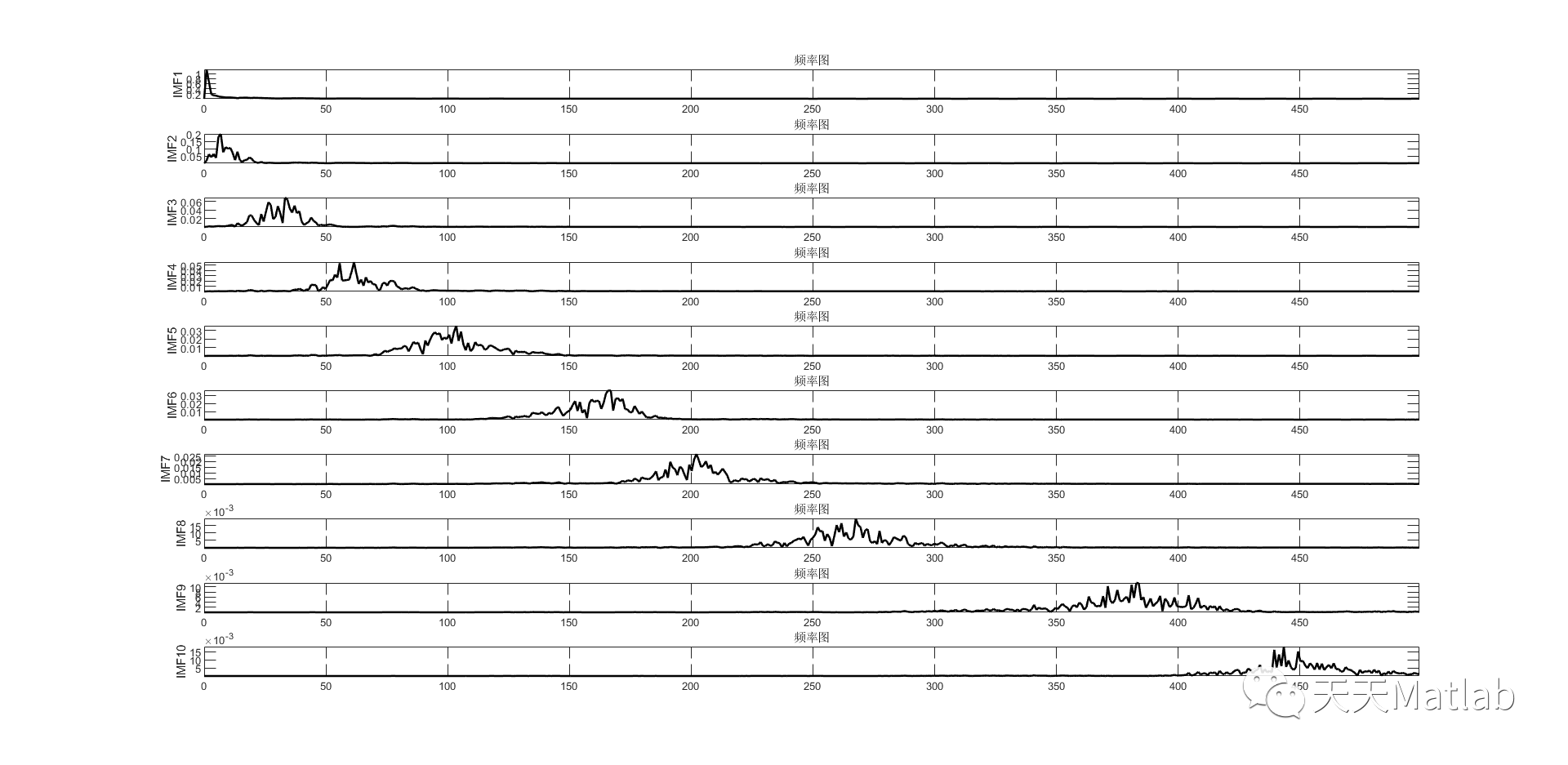
🔗 参考文献
[1] 魏永合,宫俊宇.基于CNN-LSTM-Attention的滚动轴承故障诊断[J].沈阳理工大学学报, 2022(004):041.
[2] 李爱莲,全凌翔,崔桂梅,et al.融合正余弦和柯西变异的麻雀搜索算法[J].计算机工程与应用, 2022, 58(3):9.DOI:10.3778/j.issn.1002-8331.2106-0148.
[3] 冉利民,李健伟,杜娟,等.基于变分模态分解算法的探地雷达信号去噪研究[J].世界地质, 2022(001):041.























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










