✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,
代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
在物理学应用中,无网格方法是一种广泛使用的数值计算方法,它可以解决一系列复杂的问题。其中一个重要的应用领域是解决有裂纹圆形巷道问题。本文将介绍基于无网格方法的算法流程,以解决这一具体问题。
有裂纹圆形巷道问题是指在地下巷道中存在一个或多个裂纹,通过这些裂纹会导致巷道的结构变得不稳定。为了解决这个问题,我们可以使用无网格方法来模拟裂纹的行为,并预测巷道的稳定性。
无网格方法是一种基于粒子的数值计算方法,它不需要事先定义网格,而是通过在问题域中生成大量的粒子来表示物体的形状。这些粒子之间的相互作用力可以通过一些物理模型来描述,从而模拟物体的行为。
下面是基于无网格方法解决有裂纹圆形巷道问题的算法流程:
-
初始化:定义巷道的几何形状和材料属性,并生成表示巷道的粒子集合。同时,设定裂纹的位置和初始状态。
-
计算力场:根据巷道的几何形状和材料属性,计算每个粒子所受到的力和力矩。这些力和力矩可以包括重力、惯性力、弹性力等。
-
更新裂纹:根据裂纹的行为模型,更新裂纹的位置和状态。这可以通过计算裂纹周围的应力场来实现,如果应力超过了材料的强度极限,则裂纹会扩展或扩展。
-
更新粒子状态:根据粒子所受到的力和力矩,更新粒子的位置和速度。这可以通过数值积分方法来实现,如欧拉法或Verlet法。
-
重复步骤2至4,直到达到设定的终止条件。这可以是巷道的稳定性达到一定的标准,或者是模拟的时间达到一定的长度。
通过以上算法流程,我们可以模拟有裂纹圆形巷道的行为,并预测其稳定性。这对于设计和维护地下巷道的工程师来说非常重要,可以帮助他们评估巷道的结构安全性,并采取相应的措施来增强巷道的稳定性。
总结起来,基于无网格方法的算法流程可以有效解决有裂纹圆形巷道问题。通过模拟裂纹的行为和粒子的相互作用力,我们可以预测巷道的稳定性,并为工程师提供有关巷道结构安全性的重要信息。这一方法在地下工程和物理学研究中具有广泛的应用前景。
📣 部分代码
function [gd] =gdzrbj(znyx,znd,psb,E,N)%N=32;n=32;%psb=0.25;%E=1;u=E/2/(1+psb);nbd=psb*E/(1-2*psb)/(1+psb);a=nbd+2*u;b=u;ak=zeros(1,N);Q11=zeros(N);Q12=zeros(N);Q22=zeros(N);Q21=zeros(N);ak=2*a*b/(a+b)*ak;for i=1:Nfor j=1:nak(i)= ak(i)+4*N^2/pi^3/j^3*(sin((j/N)*pi))^4*cos((i-1)*j/N*2*pi);endendQ11(1,:)=ak;for ij=2:NQ11(ij,:)=[ak(N+2-ij:N) ak(1:N+1-ij) ];endbk=zeros(1,N);bk(1,2)=1;bk(1,N)=-1;bk=bk*b^2/(a+b);Q12(1,:)=bk;for ij=2:NQ12(ij,:)=[bk(N+2-ij:N) bk(1:N+1-ij) ];endQ22=Q11;Q21=-Q12;qs=znyx-N;gd=zeros(znd*2);gdd=zeros(znd*2);for i=1:Nfor j=1:Ngd((qs+i)*2-1,(qs+j)*2-1)=Q11(i,j);gd((qs+i)*2-1,(qs+j)*2)=Q12(i,j);gd((qs+i)*2,(qs+j)*2-1)=Q21(i,j);gd((qs+i)*2,(qs+j)*2)=Q22(i,j);endend33333333;%
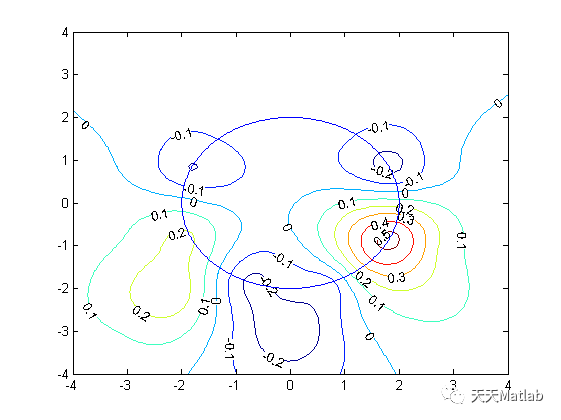
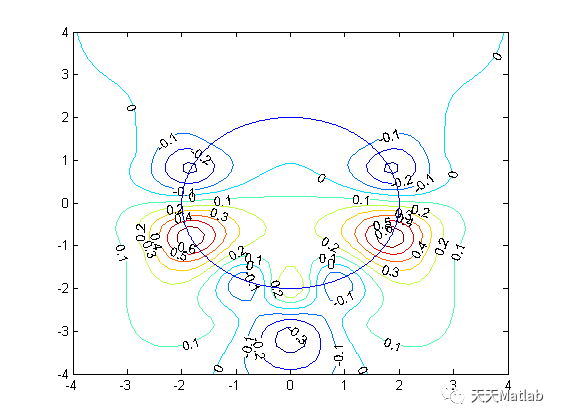
⛳️ 运行结果
🔗 参考文献
[1] 许艳.特征距离和扩充无网格法求解多裂纹问题[D].宁夏大学,2016.
[2] 许艳.特征距离和扩充无网格法求解多裂纹问题[D].宁夏大学,2015.DOI:10.7666/d.Y2861149.





 本文介绍了无网格方法在解决有裂纹圆形巷道问题中的应用,详细阐述了算法流程,包括初始化、力场计算、裂纹行为模拟和粒子状态更新,以预测巷道的结构稳定性,对地下工程设计和维护具有重要意义。
本文介绍了无网格方法在解决有裂纹圆形巷道问题中的应用,详细阐述了算法流程,包括初始化、力场计算、裂纹行为模拟和粒子状态更新,以预测巷道的结构稳定性,对地下工程设计和维护具有重要意义。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










