✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
基于MUSIC(MUltiple SIgnal Classification)算法实现均匀平面阵、直线阵和圆阵是一种常用的方法,用于估计信号源的方向或位置。以下基本的步骤框架:
-
接收阵列布置:根据具体情况选择相应的阵列结构,包括均匀平面阵、直线阵或圆阵。确保接收阵列的几何形状符合所需的定位要求。
-
采集信号数据:在已布置好的接收阵列上,采集来自的信号数据,并对其进行预处理,如去除噪声、增强信号质量等。
-
构建协方差矩阵:使用传感器数据,构建接收阵列的协方差矩阵。协方差矩阵反映了传感器之间的相互关系和接收到的信号特性。
-
MUSIC算法实施:利用MUSIC算法对协方差矩阵进行分解和分析,以估计信号源的方向或位置。该算法通过空间谱估计方法,将信号源的DOA(Direction of Arrival)与干扰噪声进行区分。
-
信号源定位:根据MUSIC算法的结果,确定信号源在空间中的位置或方向。对于均匀平阵和直线阵,可以直接获得信号源的方向角度对于圆阵,还需进行额外的计算来获取信号源的具体位置。
需要注意的是,MUSIC算法的实施涉及到信号处理、谱估计和空间波束形成等关键技术。在实际应用中,还需要考虑传感器间距离、阵列元素数目、信噪比以及接收阵列的校准和校验等方面的因素。
⛄ 部分代码
% 均匀平面阵Music算法clear all;clc;close allmx=5;my=4;%x轴和y轴阵元个数;sn=4;%信号个数dw=0.2;%半径波长比snr1=[50,50,50,50];snr=10.^(snr1/20);%信噪比(幅度表示)If=[20 30 30 50];%信号中频率(单位:MHz);f=[1.5,4.0,2.0,5.0];%信号调制频率(单位:MHz);fs=120;%采样频率(满足采样定理)(单位:MHz);N=4096;n=(1:N);%采样点数;fangwei=[10,25,135,170];%信号方位角yangjiao=[60 80 20 10]Ss=zeros(sn,N);for i=1:snfor m=1:mxfor mm=1:mydaoxiang((m-1)*my+mm,i)=exp(-j*2*pi*dw*(cos(2*pi*(m-1)/mx-fangwei(i)*pi/180)+sin(2*pi*(m-1)/mx-fangwei(i)*pi/180))*cos(yangjiao(i)*pi/180));%导向矢量endendss(i,:)=snr(i)*(1+0.3*sin(2*pi*f(i)*n/fs)).*exp(j*2*pi*n*If(i)/fs);%AM调制信号(S(t))endSignal=daoxiang*ss;noise=randn(mx*my,N);noise_h=(hilbert(noise.')).'/sqrt(2);%对噪声进行希尔伯特变化映射到复数空间x=Signal+noise_h;%接收信号(y(t))R=x*x'/N;[tzxiangliang,tzzhi]=eig(R);Nspace=tzxiangliang(:,1:mx*my-sn);%噪声子空间对应小的特征值(从小到大排列)for azi=1:1:180for ele=1:1:90for m=1:mxfor mm=1:myAQ1((m-1)*my+mm,1)=exp(-j*2*pi*dw*(cos(2*pi*(m-1)/mx-azi*pi/180)+sin(2*pi*(m-1)/mx-azi*pi/180))*cos(ele*pi/180));;endendPower=AQ1'*Nspace*Nspace'*AQ1; %在1-180度范围内进行计算P(ele,azi)=-10*log10(abs(Power));endendfigure;mesh(P);title('5*4均匀平面阵;信噪比:[50,50,50,50];距离波长比:0.5');xlabel('方位角');ylabel('仰角');zlabel('空间谱/db');grid;
⛄ 运行结果

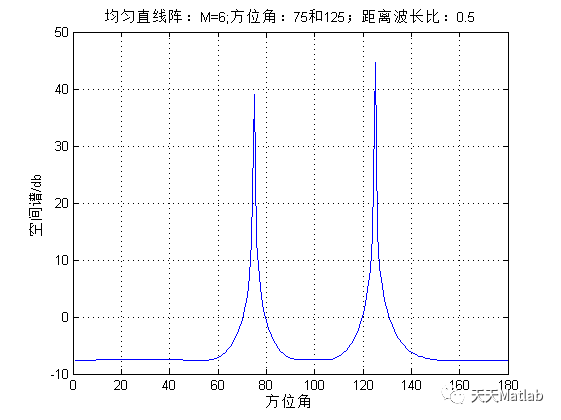
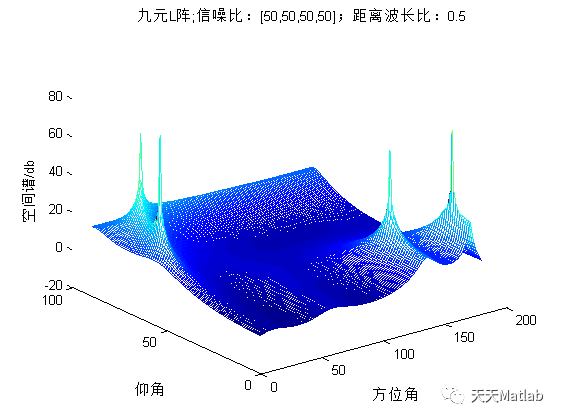
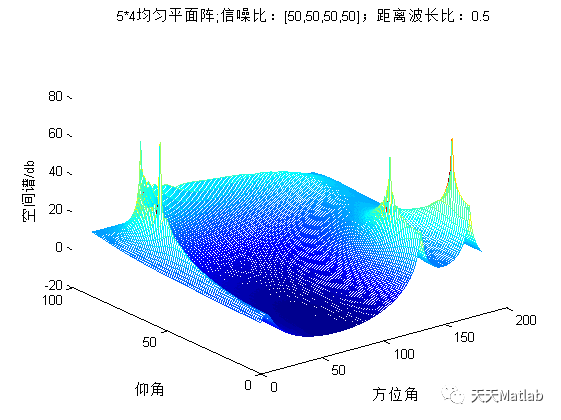





 文章介绍了基于MUSIC算法在Matlab中实现信号源方向或位置估计的过程,涉及均匀平面阵、直线阵和圆阵的布置,信号数据采集与预处理,协方差矩阵构建,以及MUSIC算法的应用。通过示例代码展示了算法在均匀平面阵中的应用,并提供了运行结果。
文章介绍了基于MUSIC算法在Matlab中实现信号源方向或位置估计的过程,涉及均匀平面阵、直线阵和圆阵的布置,信号数据采集与预处理,协方差矩阵构建,以及MUSIC算法的应用。通过示例代码展示了算法在均匀平面阵中的应用,并提供了运行结果。

















 1132
1132

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










