- 上溢出:c极其大的时候,计算ece^cec
- 下溢出:当c趋于负无穷的时候,分母是一个极小的数,导致下溢出
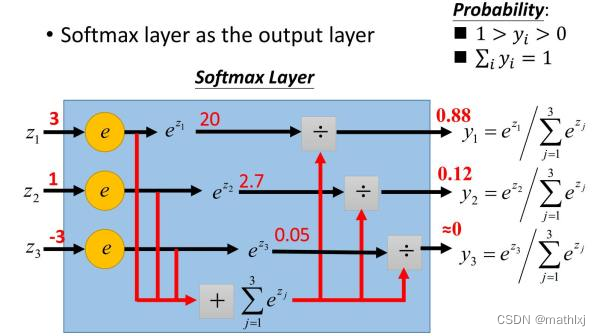
- 解决方法
令M=maxxi,i=1,2,⋯ ,nM=\max{x_i}, i=1,2,\cdots,nM=
如何防止softmax函数overflow和underflow?
最新推荐文章于 2024-12-09 14:53:17 发布
 文章讨论了在C语言中进行大数值计算时可能出现的上溢出和下溢出问题。当c值极大时,计算e^c可能会导致上溢出,而c趋于负无穷时,分母极小可能导致下溢出。为了解决这些问题,可以采用最大值策略,将函数f(x)_i的值改为其减去所有x_i中的最大值M,这种方法能保持数值稳定且理论上计算结果不变。许多数值计算库已采纳此方法来确保计算精度。
文章讨论了在C语言中进行大数值计算时可能出现的上溢出和下溢出问题。当c值极大时,计算e^c可能会导致上溢出,而c趋于负无穷时,分母极小可能导致下溢出。为了解决这些问题,可以采用最大值策略,将函数f(x)_i的值改为其减去所有x_i中的最大值M,这种方法能保持数值稳定且理论上计算结果不变。许多数值计算库已采纳此方法来确保计算精度。





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 431
431


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?







