动态规划--区间DP_区间分割动态规划-优快云博客

本文链接：https://blog.youkuaiyun.com/mathematicians/article/details/144494687

区间DP

引入

区间DP主要用于解决涉及区间分割与合并的动态规划问题。

在这类问题中，我们往往会关注一段区间上的某种性质（方案数、组合数、最大值……）

而区间DP的状态转移则是枚举区间划分的最后一步，把区间一分为二，利用小的区间求得的值求得整个区间的值

由于大区间依赖小区间，所以长度都是从小遍历到大

一起到例题中看看吧~

例题

洛谷P1880 石子合并

题目描述

在一个圆形操场的四周摆放 $N$ 堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

输入

数据的第 $1$ 行是正整数 $N$ ，表示有 $N$ 堆石子。

第 $2$ 行有 $N$ 个整数，第 $i$ 个整数 $a_i$ 表示第 $i$ 堆石子的个数。

$1\leq N\leq 100$ ， $0\leq a_i\leq 20$

输出

输出共 $2$ 行，第 $1$ 行为最小得分，第 $2$ 行为最大得分。

样例输入 #1

4
4 5 9 4

样例输出 #1

43
54

分析

在这里插入图片描述

代码

//区间dp
#include<iostream>
#include<cstring>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int dp[N][N];
int n;
int a[N];

int main()
{
	cin >> n;

	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) a[i + n] = a[i];
	for (int i = 1; i <= 2 * n; i++) a[i] += a[i - 1];

	for (int len = 2; len <= n; len++)
		for (int i = 1; i + len - 1 < 2 * n; i++)
		{
			int j = i + len - 1;
			dp[i][j] = INF;
			for (int k = i; k + 1 <= j; k++)
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + a[j] - a[i - 1]);
		}

	int mint = INF;
	for (int i = 1; i <= n; i++) mint = min(mint, dp[i][i + n - 1]);
	cout << mint << endl;

	for (int len = 2; len <= n; len++)
		for (int i = 1; i + len - 1 < 2 * n; i++)
		{
			int j = i + len - 1;
			dp[i][j] = 0;
			for (int k = i; k + 1 <= j; k++)
				dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + a[j] - a[i - 1]);
		}

	int maxt = 0;
	for (int i = 1; i <= n; i++) maxt = max(maxt, dp[i][i + n - 1]);
	cout << maxt << endl;

	return 0;

}

:::

洛谷P4342 Polygon

题目描述

多边形是一个玩家在一个有 $n$ 个顶点的多边形上的游戏，如图所示，其中 $n ＝ 4$ 。每个顶点用整数标记，每个边用符号 $+$ （加）或符号 $*$ （乘积）标记。

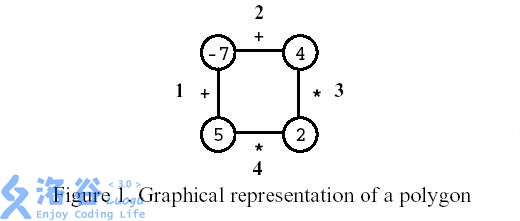
第一步，删除其中一条边。随后每一步：

选择一条边连接的两个顶点 $V_1$ 和 $V_2$ ，用边上的运算符计算 $V_1$ 和 $V_2$ 得到的结果来替换这两个顶点。

游戏结束时，只有一个顶点，没有多余的边。

如图所示，玩家先移除编号为3的边。之后，玩家选择计算编号为1的边，然后计算编号为4的边，最后，计算编号为2的边。结果是0。

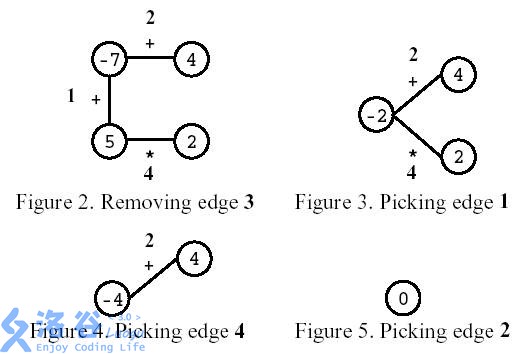
（翻译者友情提示：这里每条边的运算符旁边的数字为边的编号，不拿来计算）

编写一个程序，给定一个多边形，计算最高可能的分数。

输入

输入描述一个有 $n$ 个顶点的多边形，它包含两行。第一行是数字 $n$ ，为总边数。

第二行描述这个多边形，一共有 $2 n$ 个读入，每两个读入中第一个是字符，第二个是数字。

第一个字符为第一条边的计算符号( $t$ 代表相加， $x$ 代表相乘)，第二个代表顶点上的数字。首尾相连。

$\le n \le 50$

对于任何一系列的操作，顶点数字都在 $[- 32768, 32767]$ 的范围内。

输出

第一行，输出最高的分数。在第二行，它必须写出所有可能的被清除后的边仍能得到最高得分的列表，必须严格递增。

样例输入 #1

4
t -7 t 4 x 2 x 5

样例输出 #1

33
1 2

:::

思路
在这里插入图片描述

代码

#include <iostream>
#include <vector>

using namespace std;

const int N = 110, INF = 32768;

int n;
char c[N];
int a[N];
int f[N][N], g[N][N];

int main()
{
    cin >> n;
    
    // 破环成链
    for (int i = 1; i <= n; i ++ )
    {
        cin >> c[i] >> a[i];
        c[i + n] = c[i];
        a[i + n] = a[i];
    }
    
    for (int len = 1; len <= n; len ++ )
        for (int i = 1; i + len - 1 <= 2 * n; i ++ )
        {
            int j = i + len - 1;
            
            // 只有一个数,不用操作
            if (len == 1)
            {
                f[i][j] = g[i][j] = a[i];
                continue;
            }
            
            // 枚举分界点
            f[i][j] = -INF, g[i][j] = INF; // 初始化
            for (int k = i; k < j; k ++ )
            {
                char op = c[k + 1]; // 取操作符
                int lm = g[i][k], lM = f[i][k], rm = g[k + 1][j], rM = f[k + 1][j];
                
                if (op == 't') f[i][j] = max(f[i][j], lM + rM), g[i][j] = min(g[i][j], lm + rm);
                else 
                {
                    int m = lm * rm, M = lm * rm;
                    
                    m = min(m, lm * rM);
                    m = min(m, lM * rm);
                    m = min(m, lM * rM);
                    
                    M = max(M, lm * rM);
                    M = max(M, lM * rm);
                    M = max(M, lM * rM);
                    
                    f[i][j] = max(f[i][j], M), g[i][j] = min(g[i][j], m);
                }
            }
            
        }
        
    int res = -INF; // 最大值
    vector<int> segs; // 方案
    for (int i = 1; i <= n; i ++ ) res = max(res, f[i][i + n - 1]);
    for (int i = 1; i <= n; i ++ )
        if (f[i][i + n - 1] == res)
            segs.push_back(i);

        
    cout << res << endl;
    for (auto i : segs)
        cout << i << " ";
    
    return 0;
}

洛谷P10956 金字塔

题目描述

虽然探索金字塔是极其老套的剧情，但是有一队探险家还是到了某金字塔脚下。

经过多年的研究，科学家对这座金字塔的内部结构已经有所了解。

首先，金字塔由若干房间组成，房间之间连有通道。

如果把房间看作节点，通道看作边的话，整个金字塔呈现一个有根树结构，节点的子树之间有序，金字塔有唯一的一个入口通向树根。

并且，每个房间的墙壁都涂有若干种颜色的一种。

探险队员打算进一步了解金字塔的结构，为此，他们使用了一种特殊设计的机器人。

这种机器人会从入口进入金字塔，之后对金字塔进行深度优先遍历。

机器人每进入一个房间（无论是第一次进入还是返回），都会记录这个房间的颜色。

最后，机器人会从入口退出金字塔。

显然，机器人会访问每个房间至少一次，并且穿越每条通道恰好两次（两个方向各一次），然后，机器人会得到一个颜色序列。

但是，探险队员发现这个颜色序列并不能唯一确定金字塔的结构。

现在他们想请你帮助他们计算，对于一个给定的颜色序列，有多少种可能的结构会得到这个序列。

因为结果可能会非常大，你只需要输出答案对 $10^9$ 取模之后的值。

输入

输入仅一行，包含一个字符串 $S$ ，长度不超过 $300$ ，表示机器人得到的颜色序列。

输出

输出一个整数表示答案。

样例输入 #1

ABABABA

样例输出 #1

思路

在这里插入图片描述

代码

#include <iostream>

using namespace std;

typedef long long LL;
const int mod = 1e9, N = 310;

int n;
string s;
int dp[N][N];

int main()
{
    cin >> s;
    int n = s.size();
    
    if (n % 2 == 0) puts("0"); // 无解
    else 
    {
        for (int len = 1; len <= n; len ++ )
            for (int i = 0; i + len - 1 < n; i ++ )
            {
                int j = i + len - 1;
                if (len == 1) dp[i][j] = 1; // 边界
                else if (s[i] == s[j]) // 两端相等才有解
                    // 找符合条件的
                    for (int k = i; k < j; k ++ )
                        if (s[k] == s[i])
                            dp[i][j] = (dp[i][j] + (LL)dp[i][k] * dp[k + 1][j - 1]) % mod;
            }
            
        cout << dp[0][n - 1] << endl;
    }
    
    return 0;
}