一、了解人工智能
1、人工智能定义
人工智能(Artificial Intelligence),英文缩写为 AI,它是研究、开发用于模拟、 延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学
2、机器学习和人工智能,深度学习的关系
(1)机器学习是人工智能的一个实现途径
(2)深度学习是机器学习的一个方法发展而来
3、机器学习定义
机器学习是从数据中自动分析获得规律(模型),并利用规律对未知数据进行预测
关于机器学习定义理解:
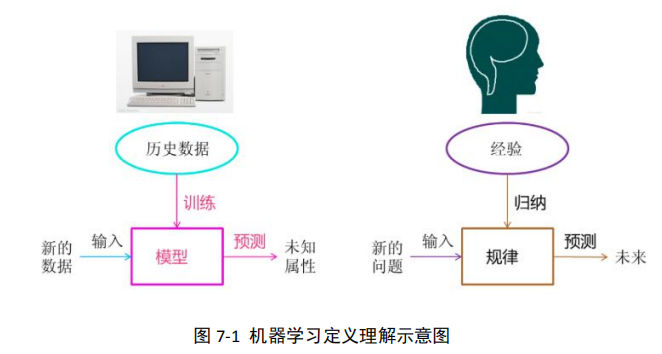
4、机器学习目标
解放生产力,如:
(1)智能客服:不知疲倦 24 小时小时作业
(2)量化投资:避免更多的编写策略、交易人员
(3)医疗:帮助医生辅助医疗 等等,都大大减小了人的功能
5、应用场景
机器学习的应用场景非常多,可以说渗透到了各个行业领域当中。医疗、航空、教育、 物流、电商等等领域的各种场景,如:
(1)挖掘、预测领域
(2)图像领域
(3)自然语言处理领域都有机器学习算法的影子
都有机器学习算法的影子
二、机器学习分类
1、无监督学习
特征与目标(标签)
(1)特征 字典中的解释为事物异于其他事物的特点,在我们机器学习中特征即样本的属性
(2)目标(标签) 机器学习中目标即需要预测的值为目标
下表为房子的信息与价格表
| 房子名称 | 房子面积 | 房子楼层 | 房子位置 | 房子价格(万元/平 米) |
|---|---|---|---|---|
| 房子 | A | 109 | 30 | 火车西站旁 |
| 房子 | B | 129 | 25 | 郊区五环外 |
| 房子 | C | 79 | 19 | xx 地铁旁 |
| 房子 | D | 96 | 3 | xx 超市旁 |
根据特征与目标(标签)的定义可以得到,其中房子名称、房子面积、房子楼层、房子 位置等属性属于特征值,而房子价格则是我们根据特征值需要预测的,那么房子价格为目标值
无监督学习定义
无监督学习是机器学习技术中的一类,用于发现数据中的模式
利用无标签的数据学习数据的分布或数据与数据之间的关系被称作无监督学习
如下表中,给出身高、体重信息后,判断每个人的体重分别属于超重、偏瘦、正常中的 哪一类?
表 xx 身高体重信息表
| 姓名 | 身高(cm) | 体重(kg) |
|---|---|---|
| 甲 | 165 | 45 |
| 乙 | 178 | 67 |
| 丙 | 155 | 65 |
| 丁 | 170 | 70 |
| X | 120 | 45 |
注意: 无监督学习没有训练集,只有一组数据,在该组数据集内寻找规律
3、监督学习
监督学习定义
从有标记的训练数据来推断一个功能的机器学习任务被称为监督学习,那么监督学习的数据集包含:特征值+目标值
监督学习研究
监督学习描述的任务是:当给定输入 x,如何通过在有标注输入和输出的数据上训练模 型而能够预测输出 y
(1)通过带有标签的训练集:训练模型;
(2)通过训练模型,输入新事件自变量 x,预测预测输出 y
例:假如你在院子里发现了这个萌萌的蘑菇,你想知道它是不是有毒啊?能不能吃呢?

分析:首先,我们通过输入了好多蘑菇的图片,训练了一个蘑菇分类器;之后我们再通 过输入图片,判断图片上的蘑菇是否有毒。这个“是否有毒分类器”就可以告诉我们,这个 蘑菇是不是入口即挂的毒鹅膏了
(1)通过大量蘑菇训练集去训练一个蘑菇分类器;
(2)输入我们要预测的蘑菇,分类器会告诉我们,这个蘑菇是够有毒
4、监督学习数据集
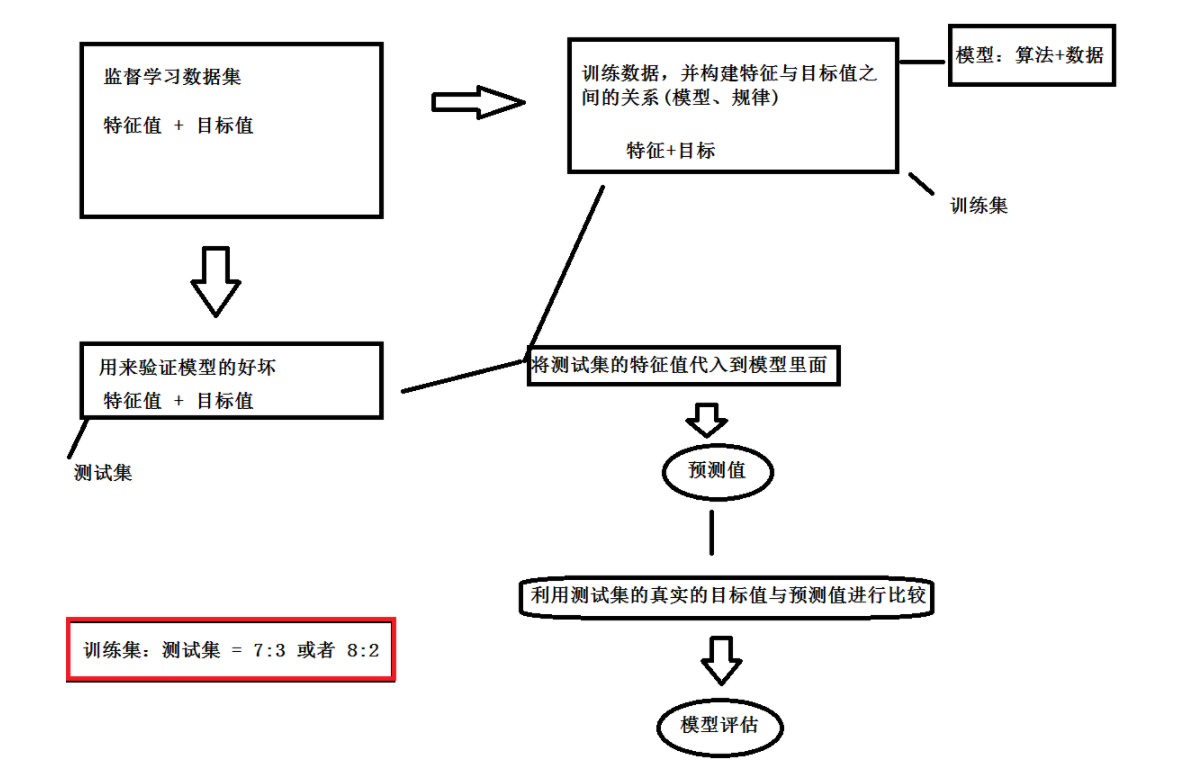
监督学习方法必须要有训练集与测试样本,在训练集中找规律,而对测试样本使用这种规律
监督学习的方法就是识别事物,识别的结果表现在给待识别数据加上了标签。因此训练 样本集必须由带标签的样本组成
何时采用哪种方法?
简单的方法就是从定义入手,有训练样本则考虑采用监督学习方法;无训练样本,则一 定不能用监督学习方法。但是,现实问题中,即使没有训练样本,我们也能够凭借自己的双 眼,从待分类的数据中,人工标注一些样本,并把它们作为训练样本,这样的话,可以把条 件改善,用监督学习方法来做。对于不同的场景,正负样本的分布如果会存在偏移(可能大 的偏移,可能比较小),这样的话,监督学习的效果可能就不如用非监督学习了
监督学习数据集可以自定义进行划分,也可以通过 sklearn 中的train_test_split 进 行划分
常用的数据集划分比例为:
训练集:70%,80%
测试集:30%,20%
自定义划分的时候,直接获取一定比例的数据集为训练集,另一部分为测试集,需要自己手动划分
而通过 sklearn 中的 sklearn.model_selection.train_test_split 进行划分的时候, 只需要传入相关参数,就可以返回对应的相关数据集
表 xx train_test_split 参数说明
| 参数名称 | 说明 |
|---|---|
| x | 数据集的特征值 |
| y | 数据集的目标值 |
| test_size | 测试集的占比,一般为[0,1]之间的 float 类型 |
| random_state | 随机数种子,不同的种子会造成不同的随机采样结果,相同的种子采样结果相同 |
5、监督学习划分
看一看,比一比:以下两组案例的特点是什么?有什么区别?
第一组例:
(1)银行贷款员需要分析数据,以搞清楚哪些贷款申请者是”安全的”,哪些是“冒险 的”?
(2)AllElectronics 的销售经理需要数据分析,以便帮助他猜测具有某些特征的客户 是否会购买新的计算机?
(3)医学研究人员希望分析乳腺癌数据,以便预测病人应当接受三种具体治疗方案中 的哪一种?
第二组例:
(1)销售经理希望预测一位给定的顾客在 AllElectronics 的一次购物期间将花多少钱?
(2)房地产开发商人希望预测 2019 年的房价范围?
(3)雷达研发人员想要根据目标的运动轨迹,预测下一时刻目标的位置坐标?
对比结果: 第一组案例的预测的目标都是离散的;第二组例的预测的目标都是连续的数值型数据, 而不是离散型的
而在监督学习中,离散预测、数值型预测为主要的预测类型,按照预测目标的不同,可 以将监督学习分位分类算法与回归算法
(1)分类算法
提取刻画重要数据类的模型,这种模型为分类器,预测分类的类标号
典型算法代表:K 最邻近算法、朴素贝叶斯、决策树算法、随机森林算法等
应用:欺诈检测、目标营销、性能预测、制造和医疗诊断
(2)回归算法
构造模型预测一个连续值函数或有序值
典型算法代表:回归分析类算法
应用:房价预测等
三、KNN 算法
1、KNN 算法原理
KNN 算法原理:
(1)计算已知类别数据集中的点与当前点之间的距离
(2)按照距离递增次序排序
(3)选择与当前距离最小的 k 个点
(4)确定前 k 个点所在类别的出现概率
(5)返回前 k 个点出现频率最高的类别作为当前点的预测分类
四、案例:算法的电影分类
下面通过改造 Peter Harrington 的《机器学习实战》中电影分类的例子,说明该算法 的用法,当然实际情况不可能这么简单
以电影分类案例来理解 KNN 算法原理:
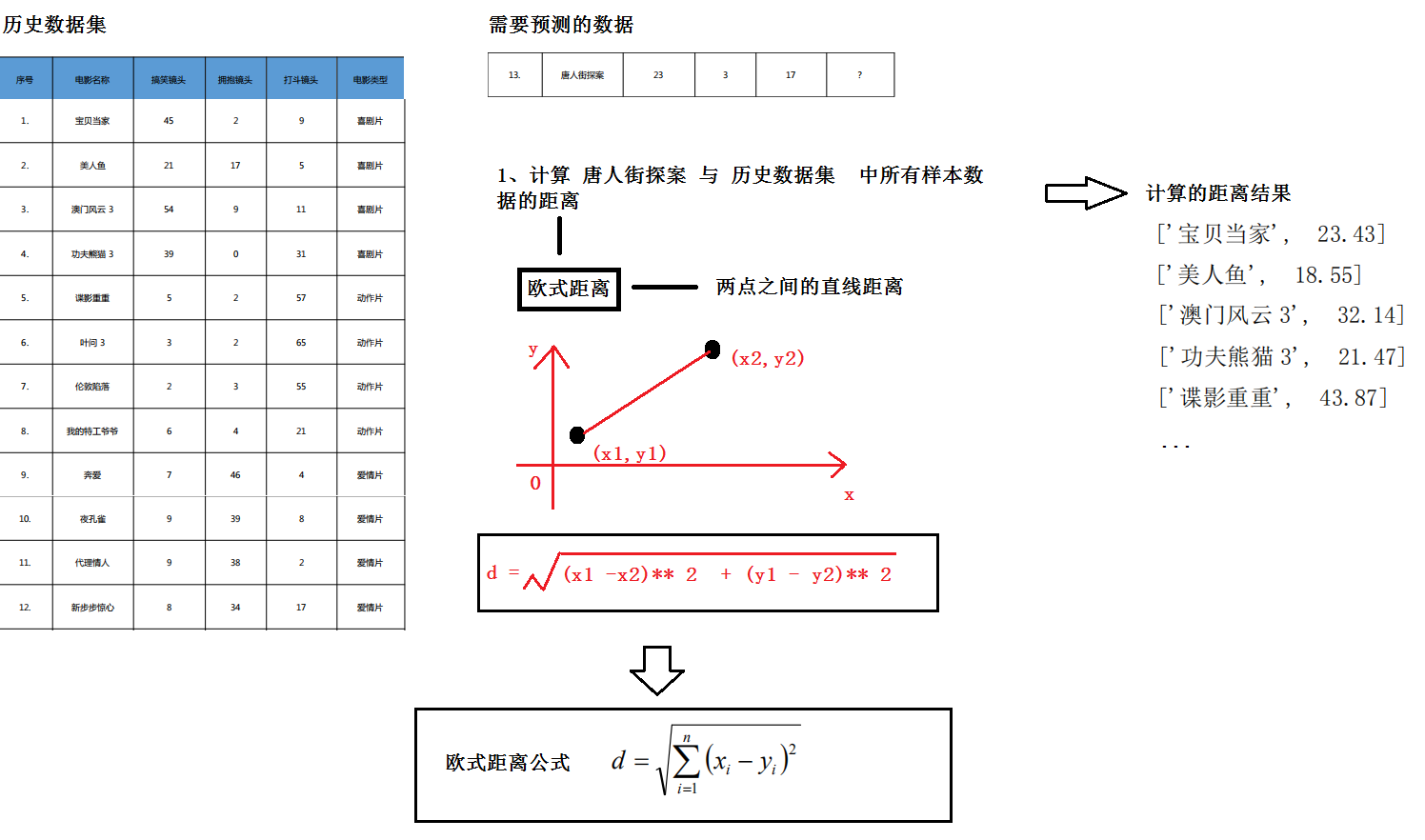
以下为电影数据表,序号 1-12 为已知的电影分类,分为喜剧片、动作片、爱情片三个 种类,使用的特征值分别为搞笑镜头、打斗镜头、拥抱镜头的数量。那么来了一部新电影《唐 人街探案》,它属于上述 3 个电影分类中的哪个类型?用 KNN 是怎么做的呢?

五、KNN 算法 API
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=“auto”)
表 xx KNeighborsClassifier 参数说明
| 参数名称 | 明 |
|---|---|
| n_neighbors | nt,可选,默认为 5,代表邻居数量 |
| algorithm | 选择{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},表示 用于计算最近邻的算法。'ball_tree’将会使用 Ball_Tree,'kd_tree’将使用 KDTree。'auto’将尝试根 据传递给 fit 方法的值来决定最合适的算法(不同的实现方式效率不同) |
将自实现的 KNN 手写字更改为 KNeighborsClassifier 来实现手写字分类
代码实现:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score # 轮廓系数
def min_max_sca(data):
"""
离差标准化来标准化数据
:param data: 需要标准化的数据
:return: 标准化之后的数据
"""
data = (data - data.min()) / (data.max() - data.min())
return data
def build_data():
"""
加载并处理数据
:return: data
"""
# 加载数据
data = pd.read_csv('./company.csv', encoding='gbk')
# print('data:\n', data)
# 使用 平均每次消费金额 平均消费周期(天) 进行聚类
# 筛选数据
data = data.loc[:, ['平均每次消费金额', '平均消费周期(天)']]
# print('data:\n', data)
# 检测缺失值
res_null = pd.isnull(data).sum()
# print('缺失值检测结果:\n', res_null)
# 异常值 ---无异常值
# 标准化数据
# 离差标准化
for column in data.columns:
data.loc[:, column] = min_max_sca(data.loc[:, column])
# print('标准化之后的数据:\n', data)
# 转化为 ndarray
data = data.values
# print('data:\n', data)
return data
def center_init(data, k):
"""
聚类中心初始化
:param data: 数据
:param k: 聚类的类别数目即聚类中心数目
:return: center
"""
# 获取data的行数
index_num = data.shape[0]
# 构建行下标数组
index = np.arange(index_num)
# 随机初始化聚类中心
# 随机在 data 选中 k个样本 作为k个中心
# 随机选择 k 行
# 参数1: 选择的数组
# 参数2:选择的数据的个数
# replace=False 不重复
mask = np.random.choice(index, k, replace=False)
print('mask:\n', mask)
# 筛选数据
center = data[mask, :]
# print('center:\n', center)
return center
def distance(v1, v2):
"""
利用欧式距离来计算两点之间的距离
:param v1: 点1
:param v2: 点2
:return: dst
"""
dst = np.sqrt(np.sum(np.power((v1 - v2), 2)))
return dst
def k_means_owns(data, k):
"""
自实现超市用户聚类
:param data: 数据
:param k: 聚类的类别
:return: center, new_data
"""
# 初始化聚类中心
center = center_init(data, k)
# 获取 data的行数
index_num = data.shape[0]
# 构建一个占位数组 --- (每一个样本的最小距离,该样本所属的簇的下标)
new_data = np.zeros(shape=(index_num, 2))
# 设置开关
flag = True
while flag:
# 打开开关
flag = False
# 计算每一个样本与每一个聚类中心的距离
for i in range(index_num):
# i :代表的是样本的行下标
# 构建一个 min_dst
min_dst = 1000000
# 构建一个 min_index(该样本最小的距离属于哪一个聚类中心)
min_index = -1
for j in range(k):
# j 代表的是 聚类中心的行下标
dst = distance(data[i, :], center[j, :])
print('dst:\n', dst)
# 比较
if dst < min_dst:
min_dst = dst
min_index = j
print('min_dst:\n', min_dst)
print('min_index:\n', min_index)
# 判断,如果该样本上一次的聚类结果与此次的聚类结果不一致时,才保存新的类别
# 如果该样本的聚类类别与上一次一致,不需要保存
if min_index != new_data[i, 1]:
# 将 最小距离 以及所属的簇 保存起来
new_data[i, 0] = min_dst
new_data[i, 1] = min_index
# 闭合开关,重新聚类
flag = True
print('new_data:\n', new_data)
if flag:
# 划分为不同的簇,计算不同簇的中心
for p in range(k):
# 确定bool数组
mask = new_data[:, 1] == p
# 获取各个簇的点
p_cluster = data[mask, :]
# 计算各个簇的中心
center[p, :] = p_cluster[:, 0].mean(), p_cluster[:, 1].mean()
# 如果上次的聚类 所有样本的聚类类别 = 以新中心为聚类中心的聚类的类别 ---->聚类结束
return center, new_data
def show_res(data, center, new_data):
"""
结果可视化
:param data: 数据
:param center: 聚类中心
:param new_data: 聚类的所属的簇
:return: None
"""
# 创建画布
plt.figure()
# 默认不支持中文 ---修改RC参数
plt.rcParams['font.sans-serif'] = 'SimHei'
# 增加字体之后变得不支持负号,需要修改RC参数让其继续支持负号
plt.rcParams['axes.unicode_minus'] = False
# 绘图
# 构建一个color_list
color_list = ['r', 'g', 'k']
# 构建一个 marker_list
marker_list = ['d', 'o', '*']
# 点的分布 --散点图
for i in range(data.shape[0]):
# i : data的行下标
plt.scatter(data[i, 0], # 横坐标
data[i, 1], # 纵坐标
c=color_list[int(new_data[i, 1])], # 颜色
marker=marker_list[int(new_data[i, 1])] # 点的样式
)
# 描绘 聚类中心
# 绘制标记
plt.plot(center[:, 0], center[:, 1], 'bX', markersize=12)
# 增加 标题
plt.title('超市用户聚类结果')
# 横轴
plt.xlabel('平均每次消费金额')
# 纵轴
plt.ylabel('平均消费周期(天)')
# 保存
plt.savefig('./超市用户聚类结果.png')
# 展示
plt.show()
def k_means_sklearn(data, k):
"""
基于sklearn中KMeans来实现用户聚类
:param data: 数据
:param k: 聚类的类别数目
:return:
"""
# 1、实例化算法对象
# n_clusters :聚类类别的数目
# 'k-means++' :教优的方式初始化聚类中心,加速迭代
km = KMeans(n_clusters=k)
# 2、训练数据并构建模型
km.fit(data)
# 3、进行预测
y_predict = km.predict(data)
# 获取最终的聚类中心
center = km.cluster_centers_
return y_predict, center
def show_res_sklearn(data, y_predict, center):
"""
sklearn中k-means聚类结果可视化
:param data: 数据
:param y_predict:预测值
:param center: 聚类中心
:return: None
"""
# 创建画布
plt.figure()
# 默认不支持中文 ---修改RC参数
plt.rcParams['font.sans-serif'] = 'SimHei'
# 增加字体之后变得不支持负号,需要修改RC参数让其继续支持负号
plt.rcParams['axes.unicode_minus'] = False
# 绘图
# 构建一个color_list
color_list = ['r', 'g', 'k']
# 构建一个 marker_list
marker_list = ['d', 'o', '*']
# 点的分布 --散点图
for i in range(data.shape[0]):
# i : data的行下标
plt.scatter(data[i, 0], # 横坐标
data[i, 1], # 纵坐标
c=color_list[y_predict[i]], # 颜色
marker=marker_list[y_predict[i]] # 点的样式
)
# 描绘 聚类中心
# 绘制标记
plt.plot(center[:, 0], center[:, 1], 'bX', markersize=12)
# 增加 标题
plt.title('超市用户聚类结果')
# 横轴
plt.xlabel('平均每次消费金额')
# 纵轴
plt.ylabel('平均消费周期(天)')
# 保存
plt.savefig('./超市用户聚类结果_sklearn.png')
# 展示
plt.show()
def main():
"""
主函数
:return:
"""
# 1、加载数据,并对数据进行数据处理
data = build_data()
print('数据:\n', data)
# # 2、进行使用k-means算法进行用户聚类
# # 确定聚类类别
k = 3
# center, new_data = k_means_owns(data, k)
#
# print('最终的聚类中心center:\n', center)
# print('所有样本所属的类别:\n', new_data[:, 1])
#
# # 3、结果可视化
# show_res(data, center, new_data)
# 2、基于sklearn中的KMeans实现超市用户聚类
y_predict, center = k_means_sklearn(data, k)
print('获取预测值:\n', y_predict)
print('获取聚类中心:\n', center)
# 聚类算法的评估
# 轮廓系数 ----越趋于1,效果越好
# 计算量非常,容易出现内存不够这样的错误
# 参数1 数据的特征值
# 参数2 预测值
score = silhouette_score(data, y_predict)
print('此时的轮廓系数为:\n', score)
# 3、结果可视化
show_res_sklearn(data, y_predict, center)
if __name__ == '__main__':
main()
六、案例:手写字识别案例
如何使用 knn 算法对手写识别数据进行分类,这里构造的分类系统只能识别数字 0 到 9, 数字经图形处理软件处理成具有相同的色彩和大小,宽高为 32x32 像素,为了便于处理,已 将图像转换为文本格式,其效果图如下:

数据有两个目录,其中目录 trainingDigits 中包含了 1934 个例子,命名规则如 9_45.txt,表示该文件的分类是 9,是数字 9 的第 45 个实例,每个数字大概有 200 个实例。 testDigits 目录中包含 946 个例子。使用 trainingDigits 中的数据作为训练集,使用 testDigits 中的数据作为测试集测试分类的效果。两组数据没有重叠。利用数据集预测图 中应该是哪个数字?
代码实现:
import os
import numpy as np
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
def build_data(dir_name):
"""
数据加载及处理
:param dir_name: 文件夹的名称
:return: 数据集
"""
# 对文件夹处理
# 获取文件夹里面所有的文件名称
file_name_list = os.listdir(dir_name)
print('所有的文件名称:\n', file_name_list)
# 构建一个数据集来存储所有的样本数据
data = np.zeros(shape=(len(file_name_list), 1025))
# 循环对每一个文件进行处理 ---文件名的位置即转化为数据集之后所对应的行下标
for file_name_index, file_name in enumerate(file_name_list):
# file_name_index : 文件名的位置(下标) ---> 转化为数据集之后所对应的行下标
# file_name : 文件名称
# 加载 file_name 中的内容
# (1)with ... open ....
# (2) np.loadtxt
# (3) pd.read_table
file_data = np.loadtxt(dir_name + '/' + file_name, dtype=np.str)
# file_data : 文件内容,形状为一维数组(32,),每一个元素为长度32的01字符串
# print('file_data:\n', file_data)
# print('file_data:\n', file_data.shape)
# 准备一个 32*32的 二维数组 来占位
arr = np.zeros(shape=(32, 32))
# 接下来 对 文件内的 file_data进行转化
# 遍历
for file_content_index, file_content in enumerate(file_data):
# file_content_index : file_data中的元素的下标 -------> 二维数组的行下标
# file_content: file_data中的每一个元素, ----->二维数组中的行元素
# print('file_content_index:\n', file_content_index)
# print('file_content:\n', file_content)
# 将 file_content(长度为32的01字符串) ----> 数值型(长度为32的简单的01的列表)
# (1) 列表推导式
# single_arr = [int(i) for i in file_content]
# print('single_arr:\n', single_arr)
# (2) map方法
# 参数1:函数
# 参数2: 可迭代对象, 将可迭代对象中的每一个元素都代入参数1的函数中去
# 返回值: map对象
single_arr = list(map(int, file_content))
# print('single_arr:\n', single_arr)
# 将 single_arr 加入到 arr 中 指定的行
arr[file_content_index, :] = single_arr
# print('将单个文件转化为32*32的数值型数组的结果为:\n', arr)
# 接下来将 32*32 的数值型二维数组 展开为一维
feature = arr.ravel() # feature 形状:(1024,) # 特征值
# print('feature:\n', feature)
# print('feature:\n', feature.shape)
# 获取目标值
target = int(file_name.split('_')[0])
# 组合 特征 + 目标值
simple = np.concatenate((feature, [target]), axis=0)
# print('simple:\n', simple)
# print('simple:\n', simple.shape)
# 将每一个样本 加入到 数据集data中
data[file_name_index, :] = simple
print('数据集:\n', data)
print('数据集:\n', data.shape)
return data
def save_data(file_data, file_name):
"""
保存数据
:param file_data: 需要保存的数据
:param file_name: 文件的名称
:return:None
"""
# 创建文件夹
if not os.path.exists('./data/'):
os.makedirs('./data/')
# 保存文件
np.save('./data/' + file_name, file_data)
def load_data():
"""
加载数据
:return: train,test
"""
# 构建返回值列表
file_list = []
file_name_list = os.listdir('./data/')
# 遍历
for file_name in file_name_list:
file = np.load('./data/' + file_name)
# 加入到 file_list
file_list.append(file)
return file_list
def distance(v1, v2):
"""
基于欧式距离公式计算两点之间的距离
:param v1: 点1
:param v2: 点2
:return: dst
"""
dst = np.sqrt(np.sum(np.power((v1 - v2), 2)))
return dst
def knn_owns(train, test, k):
"""
基于knn算法的手写数字识别分类
:param train: 训练集数据
:param test: 测试集数据
:param k: 邻居个数
:return:
"""
# 拆分数据集
train_x = train[:, :1024]
train_y = train[:, 1024]
test_x = test[:, :1024]
test_y = test[:, 1024]
# 设置一个计数器
count = 0
# 对每一个测试集的样本,都应该执行KNN算法识别分类过程
for i in range(test.shape[0]):
# i 代表的是 测试集的行数,测试集的样本下标
# 构建一个dst_arr 来保存单个测试样本 与所有训练样本的距离
dst_arr = np.zeros(shape=(train.shape[0], 1))
for j in range(train.shape[0]):
# j 代表的是训练集的行数,训练集的样本下标
# 计算 测试样本 与所有训练样本的距离
dst = distance(train_x[j, :], test_x[i, :])
# print('dst:\n', dst)
# 将该距离保存起来
dst_arr[j, 0] = dst
# 此时 dst_arr保存的是 距离
# print('dst_arr:\n', dst_arr)
# 将距离 和 训练集的 类别 进行组合
arr = np.concatenate((dst_arr, train_y.reshape((-1, 1))), axis=1)
# print('arr:\n', arr)
# 将arr 转化为df
df = pd.DataFrame(data=arr,
columns=['dist', 'type'])
# print('df:\n', df)
# 排序
df = df.sort_values(by='dist', ascending=True)
# print('df:\n', df)
# 获取最近的k个邻居
df = df.head(k)
# 获取类别的众数
mode = df.loc[:, 'type'].mode()[0]
# print('mode:\n', mode)
# 预测值为mode
y_predict = mode
# 和真实的 目标值进行对比
if y_predict == test_y[i]:
# 说明预测准确
count += 1
# 获取预测准确的元素的个数
print('count:\n', count)
# 准确率
score = count / test.shape[0]
print('此时的准确率为:', score)
def knn_sklearn(train, test, k):
"""
基于sklearn中KNN算法对手写数字的识别分类
:param train: 训练集
:param test: 测试集
:param k: 邻居个数
:return: predict, score
"""
# 1、实例化算法对象
# n_neighbors:邻居个数
# weights: 权重 默认为:uniform,表示都相等,
# 如果为distance ---权重为距离倒数
# 也可以自定高斯权重
# metric :默认为:'minkowski'---闵可夫斯基距离
# p : 当p=1时,为 曼哈顿距离,当p=2时,为欧式距离,当p>2时,为切比雪夫距离
# n_jobs: 默认为1,表示单进程,如果为-1,表示开始使用所有处理器
# algorithm :查找邻居的算法方式。存在:kd_tree,ball_tree,brute --auto:代表在上述三种算法中找一个最合适的算法。
knn = KNeighborsClassifier(n_neighbors=k)
# 2、训练数据并构建模型
# 参数:训练集特征值
# 参数:训练集目标值
knn.fit(train[:, :1024], train[:, 1024])
# 3、预测
# 参数: 测试集的特征值
predict = knn.predict(test[:, :1024])
# 获取准确率
# 参数:测试集的特征值
# 参数:测试集的目标值
score = knn.score(test[:, :1024], test[:, 1024])
return predict, score
def show_res(k_list, score_list):
"""
结果可视化---描述的是:k值与准确率score的变化关系
:param k_list: 邻居个数列表
:param score_list: 准确率列表
:return: None
"""
# 1、创建画布
plt.figure()
# 默认不支持中文 ---修改RC参数
plt.rcParams['font.sans-serif'] = 'SimHei'
# 增加字体之后变得不支持负号,需要修改RC参数让其继续支持负号
plt.rcParams['axes.unicode_minus'] = False
# 2、绘制图形
plt.plot(k_list, score_list, color='r', marker='*', markersize=12, linestyle='-.')
# 增加标题
plt.title('随着k的变化准确率的变化趋势')
# 增加横轴名称
plt.xlabel('k值')
# 纵轴名称
plt.ylabel('score值')
# 保存
plt.savefig('./随着k的变化准确率的变化趋势.png')
# 3、图形展示
plt.show()
def main():
"""
主函数
:return:
"""
# # 1、数据加载 及处理
# train = build_data('./trainingDigits')
# test = build_data('./testDigits')
#
# # 将 train test 保存起来
# save_data(train, 'train')
# save_data(test, 'test')
# 加载 数据
test, train = load_data()
print('train:\n', train)
print('train:\n', train.shape)
print('test:\n', test)
print('test:\n', test.shape)
# 2、KNN识别分类
# 确定邻居个数
# k = 5
# knn_owns(train, test, k)
# 构建一个k_list
k_list = [5, 6, 7, 8, 9, 10]
# 在构建一个score_list
score_list = []
for k in k_list:
# k = 5
predict, score = knn_sklearn(train, test, k)
print('当k=' + str(k) + '时,此时的预测值为:\n', predict)
print('当k=' + str(k) + '时,此时的准确率为:\n', score)
score_list.append(score)
# 结果可视化
show_res(k_list, score_list)
if __name__ == '__main__':
main()
以下为随着 k 的变化,准确率 score 的变化趋势图:
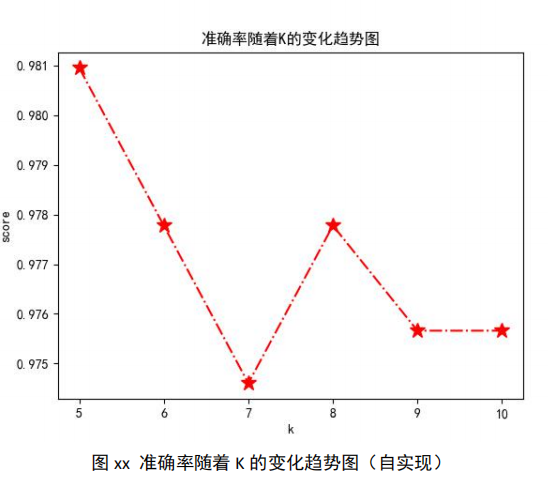
七、KNN算法总结
1、KNN 属于惰性学习(lazy-learning)
这是与急切学习(eager learning)相对应的,因为 KNN 没有显式的学习过程!也就是 说没有训练阶段,从上面的例子就可以看出,数据集事先已有了分类和特征值,待收到新样本后直接进行处理
**2、KNN 的计算复杂度较高 **
我们从上面的例子可以看到,新样本需要与数据集中每个数据进行距离计算,计算复杂 度和数据集中的数据数目 n 成正比,也就是说,KNN 的时间复杂度为 O(n),因此 KNN 一般适 用于样本数较少的数据集
3、k 取不同值时,分类结果可能会有显著不同
k 值选择中,如果设置较小的 k 值,说明在较小的范围内进行训练和统计,误差较大且 容易产生过拟合的情况;k 值较大时意味着在较大的范围中学习,可以减少学习的误差,但 是在其统计范围变大了,说明模型变简单了,容易在预测的时候发生分类错误
上例中,如果 k 取值为 k=1,那么分类就是动作片,而不是喜剧片。一般 k 的取值不超 过 20,上限是 n 的开方
KNN 算法的主要缺点: 在各分类样本数量不平衡时误差较大;由于其每次比较都要遍历整个训练样本集来计算相似度,所以分类的效率较低,时间和空间的复杂度较高;k 值的选择不合理,可能导致结 果的误差较大;在原始 KNN 模型中没有权重概念,所有特征采用相同的权重参数,这样计算出来的相似度易产生误差
八、KNN算法优化
问题:观察下图,我们看到,对于位置样本 X,通过 KNN 算法,我们显然可以得到 X 应 属于红点,但对于位置样本 Y,通过 KNN 算法我们似乎得到了 Y 应属于蓝点的结论,而这个 结论直观来看并没有说服力
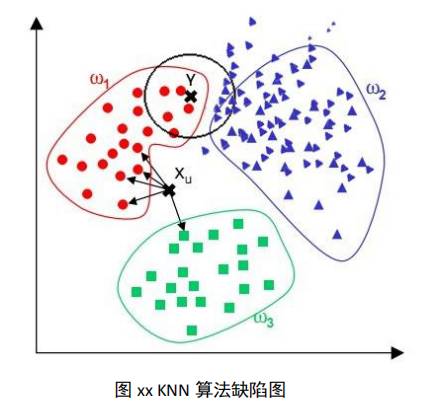
由上图可见:该算法在分类时有个重要的不足是,当样本不平衡时,即:一个类的样本 容量很大,而其他类样本数量很小时,很有可能导致当输入一个未知样本时,该样本的 K 个邻居中大数量类的样本占多数。 但是这类样本并不接近目标样本,而数量小的这类样本 很靠近目标样本。这个时候,我们有理由认为该位置样本属于数量小的样本所属的一类,但 是,KNN 却不关心这个问题,它只关心哪类样本的数量最多,而不去把距离远近考虑在内, 因此,我们可以采用权值的方法来改进。和该样本距离小的邻居权值大,和该样本距离大的 邻居权值则相对较小,由此,将距离远近的因素也考虑在内,避免因一个样本过大导致误判 的情况
从算法实现的过程大家可以发现,该算法存两个严重的问题:
第一个是需要存储全部的训练样本,
第二个是需要进行繁重的距离计算量
对此,提出以下应对策略:
其基本思想是:将样本集按近邻关系分解成组,给出每组质心的位置,以质心作为代表 点,和未知样本计算距离,选出距离最近的一个或若干个组,再在组的范围内应用一般的 knn 算法。由于并不是将未知样本与所有样本计算距离,故该改进算法可以减少计算量,但 并不能减少存储量






















 951
951

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








