62. Unique Paths (M)

最新推荐文章于 2025-12-24 16:48:10 发布

原创最新推荐文章于 2025-12-24 16:48:10 发布 · 117 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#排列组合 #动态规划

LeetCode 专栏收录该内容

202 篇文章

订阅专栏

本文探讨了一个机器人在限定网格内从左上角到右下角的唯一路径数量问题，提出了解决方案，包括组合数和动态规划方法，并给出了具体的代码实现。

Unique Paths (M)

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?
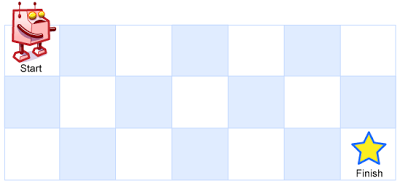
在这里插入图片描述
Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

题意

在矩形中找到一条路径，起点为左上顶点，终点为右下顶点，路径中只能向右或向下走，要求统计不同路径的个数。

思路

组合数：因为每次只能向右或向下走，所以符合条件的路径的长度必然是 m+n-2，其中有 m-1 个点是向右走，n-1 个点是向下走，问题就转化为了在 m+n-2 个点中找出 m-1 个点(或找出 n-1 个点，都一样)，求 $C_{m+n-2}^{m-1}$ 的值。
组合数求值可以用公式： $Cnm=n!m!(n−m)!C_n^m=\frac{n!}{m!(n-m)!}$ ，也可以用递推公式计算： $C_n^m=C_{n-1}^{m-1}+C_{n-1}^m$ 。

动态规划：dp[i][j]记录可以到达位置(i, j)的路径的数目，因为(i, j)只可能从(i, j-1)向右走到达，或者从(i-1, j)向下走到达，所以有 $d p [i] [j] = d p [i] [j - 1] + d p [i - 1] [j]$ 。
注意到dp[i][j]只与左边和上边的dp有关，且我们的目标只是为了得到最后一行最后一列的dp，所以可以用滚动数组对上述过程进行空间优化，无需使用二维数组。

代码实现 - 组合数

public int uniquePaths(int m, int n) {
        return calculate(m + n - 2, m - 1);
    }

    private int calculate(int n, int m) {
        double ans = 1.0;
        while (m >= 1) {
            ans *= 1.0 * n-- / m--;
        }
        return (int) Math.round(ans);
    }

代码实现 - 动态规划

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[n][m];
        dp[0][0] = 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (i != 0 || j != 0) {
                    dp[i][j] = findDP(dp, i - 1, j) + findDP(dp, i, j - 1);
                }
            }
        }
        return dp[n - 1][m - 1];
    }

    private int findDP(int[][] dp, int i, int j) {
        if (i < 0 || j < 0) {
            return 0;
        }
        return dp[i][j];
    }
}

代码实现 - 滚动数组优化

class Solution {
    public int uniquePaths(int m, int n) {
        int[] dp = new int[m];
        dp[0] = 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
            	dp[j] = dp[j] + (j > 0 ? dp[j - 1] : 0);
            }
        }
        return dp[m - 1];
    }
}