栈(Stack)

栈(Stack)

栈是一种先进后出（FILO，First in last out）或后进先出（LIFO，Last in first out）的数据结构。

• 单向链表：可以利用一个单链表来实现栈的数据结构。而且，因为我们都只针对栈顶元素进行操作，所以借用单链表的头就能让所有栈的操作在 O(1) 的时间内完成。

• Stack：是Vector的子类，比Vector多了几个方法

• Java中的Vector是一个动态数组类，它实现了List接口。与普通数组相比，Vector的大小是可变的，可以根据需要动态调整。Vector还提供了许多方法来操作和访问其中的元素，如添加、删除、查找等。Vector是线程安全的，可以在多线程环境下使用。

public class Stack<E> extends Vector<E> {
        // 把元素压入栈顶
        public E push(E item) {
            addElement(item);
            return item;
        }
    
        // 弹出栈顶元素
        public synchronized E pop() {
            E obj;
            int len = size();
            obj = peek();
            removeElementAt(len - 1);
            return obj;
        }
    
        // 访问当前栈顶元素，但是不拿走栈顶元素
        public synchronized E peek() {
            int len = size();
            if (len == 0)
                throw new EmptyStackException();
            return elementAt(len - 1);
        }
    
  // 测试堆栈是否为空
        public boolean empty() {
            return size() == 0;
        }
        
        // 返回对象在堆栈中的位置，以1为基数
        public synchronized int search(Object o) {
            int i = lastIndexOf(o);
            if (i >= 0) {
                return size() - i;
            }
            return -1;
        }
}

基本操作（失败时：add/remove/element为抛异常，offer/poll/peek为返回false或null）

• E push(E)：把元素压入栈

• E pop()：把栈顶的元素弹出

• E peek()：取栈顶元素但不弹出

• boolean empty()：堆栈是否为空测试

• int search(o)：返回对象在堆栈中的位置，以 1 为基数

应用场景

在解决某个问题的时候，只要求关心最近一次的操作，并且在操作完成了之后，需要向前查找到更前一次的操作。

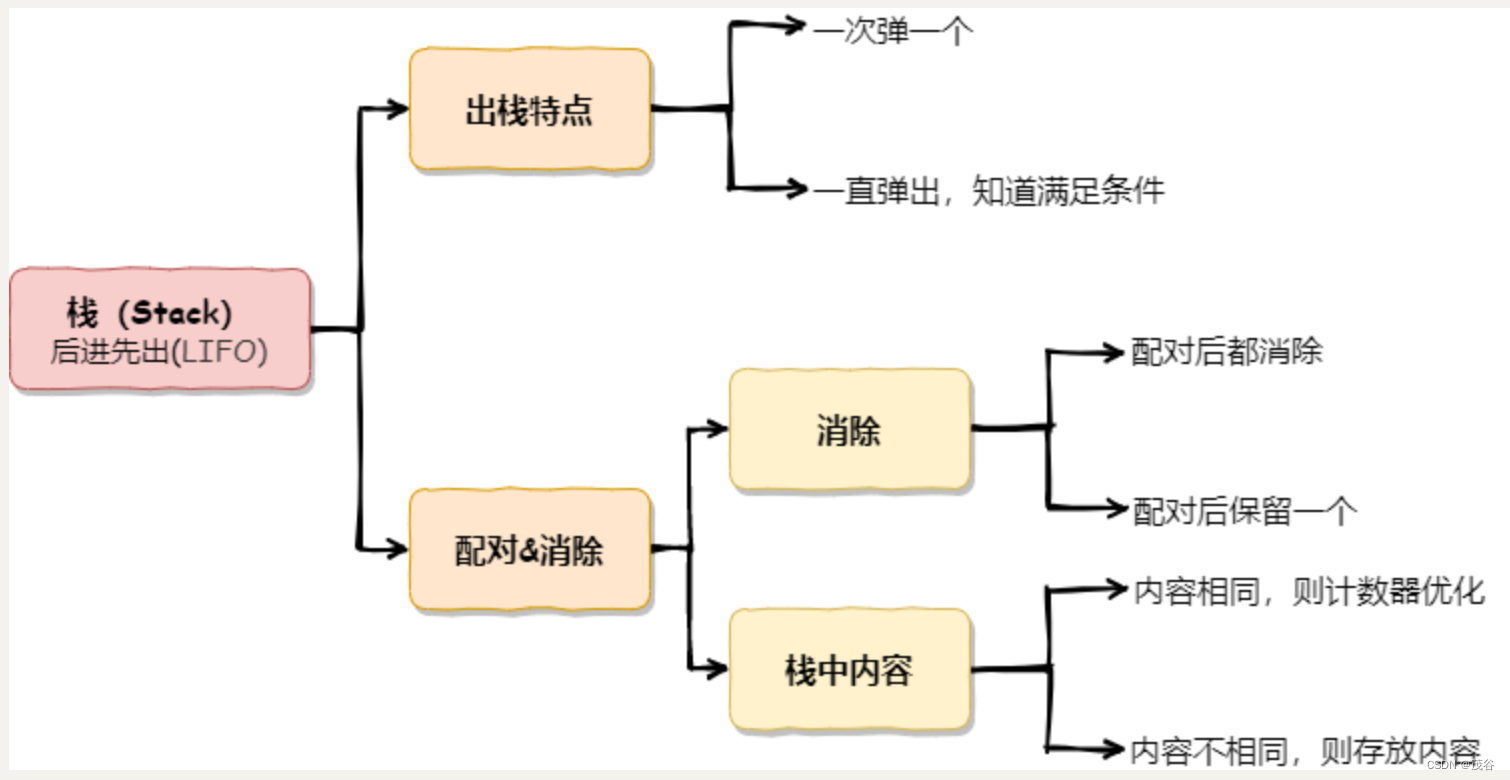
案例一：判断字符串是否有效 (算数运算符)

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。有效字符串需满足：

• 左括号必须用相同类型的右括号闭合

• 左括号必须以正确的顺序闭合

• 空字符串可被认为是有效字符串

解题思路：利用一个栈，不断地往里压左括号，一旦遇上了一个右括号，我们就把栈顶的左括号弹出来，表示这是一个合法的组合，以此类推，直到最后判断栈里还有没有左括号剩余。

案例二：每日温度

根据每日气温列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。

解题思路

• 思路 1：最直观的做法就是针对每个温度值向后进行依次搜索，找到比当前温度更高的值，这样的计算复杂度就是 O(n2)。

• 思路 2：可以运用一个堆栈 stack 来快速地知道需要经过多少天就能等到温度升高。从头到尾扫描一遍给定的数组 T，如果当天的温度比堆栈 stack 顶端所记录的那天温度还要高，那么就能得到结果。