利用paddlepaddle框架实现简单线性回归

原创已于 2024-10-04 15:37:46 修改 · 1.2k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #python

于 2024-10-04 15:35:57 首次发布

深度学习专栏收录该内容

2 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

文章目录

前言

这个案例实现了一个简单的线性回归模型，使用 PaddlePaddle 框架进行训练和预测。让读者熟悉paddlepaddle框架的模型流程。

提示：以下是本篇文章正文内容，下面案例可供参考

一、paddlepaddle是什么？

PaddlePaddle（PArallel Distributed Deep LEarning）是百度开发的一个开源深度学习框架。它提供了多种工具和库，使得研究人员和开发者能够高效地构建、训练和部署深度学习模型PaddlePaddle 被广泛应用于各种行业和场景，如自动驾驶、医疗影像、语音识别等。

二、使用步骤

1.运行环境和引入库

运行环境：

Python版本：python3.7

框架版本：PaddlePaddle 1.8.0

（建议在AI Studio中运行）

引入库代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
import paddle
import paddle.fluid as fluid

fluid 是 PaddlePaddle 的一个子模块，主要用于定义和训练深度学习模型，提供了一系列用于构建神经网络、优化算法和数据处理的工具。

2.准备数据样本

代码如下（示例）：

train_data = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]).astype('float32')
y_true = np.array([[5.0], [5.5], [6.0], [6.8], [6.8]]).astype('float32')

3.定义模型

##定义占位符张量
x=fluid.layers.data(name='x', shape=[1], dtype='float32')
y=fluid.layers.data(name='y', shape=[1], dtype='float32')
y_predict=fluid.layers.fc(input=x,#输入张量
                          size=1,#输出值的个数
                          act=None)

前两行代码定义了两个占位符张量，分别是 x 和 y，用于存放输入数据和目标值（标签）。每个占位符都有以下参数：

name: 占位符的名称。x 是输入特征，y 是目标输出（标签）。
shape: 定义了输入数据的形状。[1] 表示输入是一个单独的特征（如单个数据的值）。
dtype: 数据类型。'float32' 表示数据是32位浮点数。

最后一行代码定义了一个全连接层（fc），即一个线性层，用于对输入的 x 进行线性变换并输出预测值 y_predict。参数解释如下：

input: 输入数据（即 x），输入到网络的特征。
size: 输出的维度，这里设置为 1，表示输出是一个单独的值（预测的结果）。
act: 激活函数。None 表示没有激活函数，仅执行线性变换。在线性回归中，通常不使用激活函数。

4.定义损失函数，优化器

cost=fluid.layers.square_error_cost(input=y_predict,#预测值
                                    label=y)#标签值
avg_cost=fluid.layers.mean(cost)#求均值，均方差
optimizer=fluid.optimizer.SGD(learning_rate=0.01)#优化器
optimizer.minimize(avg_cost)#指定优化的目标函数

第一行代码定义了一个损失函数，采用的是平方误差损失。在回归问题中，常常用平方误差来衡量模型预测值和实际值之间的差距。具体解释如下：

input=y_predict: 这是模型的预测值。
label=y: 这是模型的真实值（标签）。

平方误差的公式为： $SE=\left (y_{predict}-y_{ture} \right )^{2}$ 表示预测值与真实值之间的误差的平方。

第二行代码求均方误差，因为训练一个模型时不会只用单个样本，而是用一个批量的数据集。因此，我们希望得到所有样本的平均损失。

平均损失（均方误差，MSE）的公式为： $MSE=\frac{1}{n}\sum_{i=1}^{n}\left ( y_{predict}^{(i)}-y_{true} ^{(i)}\right )^{2}$

第三行代码定义了一个随机梯度下降（SGD）优化器，学习率设定为 0.01。优化器的作用是在训练过程中调整模型的参数（例如权重和偏置），使得损失函数的值最小化。

SGD: 这是最经典的优化算法，按照梯度下降法更新参数。它根据损失函数的梯度来调整参数，使得损失逐渐减小。
learning_rate=0.01: 这是学习率，控制参数更新的步伐。学习率太大可能导致训练不稳定，太小则训练速度过慢。

第四行代码表示用优化器来最小化损失函数 avg_cost，并执行反向传播。其作用是在训练过程中，根据误差的梯度更新模型的参数，使得模型的预测结果与真实值越来越接近。

5.训练

costs=[]#存储损失值
iters=[]#存储迭代次数
values=[]#存储预测值
params={"x":train_data,"y":y_true}
place=fluid.CPUPlace()
exe = fluid.Executor(place)
exe.run(fluid.default_startup_program())#初始化

for i in range(200):
    outs=exe.run(program=fluid.default_main_program(),
                 feed=params,#参数字典
                 fetch_list=[y_predict,avg_cost])#返回预测值，损失函数的值
    iters.append(i)#存储迭代次数
    costs.append(outs[1][0])#存储损失值
    print("i:",i,"cost:",outs[1][0])#打印损失值

这段代码是训练线性回归模型的核心部分，主要完成了模型的训练过程。

这里使用了字典 params 来指定输入的训练数据，键值对 x 对应输入数据，y 对应真实的标签数据。train_data 是输入数据，y_true 是对应的真实值。

选择运行环境和初始化执行器

fluid.CPUPlace() 表示使用 PaddlePaddle 的 CPU 设备来执行计算。
fluid.Executor(place) 创建了一个执行器 exe，用于在指定的硬件设备（CPU 或 GPU）上执行计算。
exe.run(fluid.default_startup_program()) 运行 PaddlePaddle 的启动程序，初始化模型中的参数（例如权重和偏置），为训练做好准备。

运行模型：

exe.run()：执行当前的计算图（模型）。
program=fluid.default_main_program()：运行默认的主程序，即当前定义的计算图（包括模型的前向计算和损失的反向传播）。
feed=params：将训练数据 params 传入模型。
fetch_list=[y_predict, avg_cost]：指定要获取的计算结果，这里返回了模型的预测值 y_predict 和平均损失值 avg_cost。

6.绘图

# 线性模型可视化
tmp = np.random.rand(10, 1)  # 生成10行1列的均匀随机数组
tmp = tmp * 2  # 范围放大到0~2之间
tmp.sort(axis=0)  # 排序
x_test = np.array(tmp).astype("float32")
params = {"x": x_test, "y": x_test}  # y参数不参加计算，只需传一个参数避免报错
y_out = exe.run(feed=params, fetch_list=[y_predict.name])  # 预测
y_test = y_out[0]

# 损失函数可视化
plt.figure("Trainging")
plt.title("Training Cost", fontsize=24)
plt.xlabel("Iter", fontsize=14)
plt.ylabel("Cost", fontsize=14)
plt.plot(iters, costs, color="red", label="Training Cost")  # 绘制损失函数曲线
plt.grid()  # 绘制网格线
plt.savefig("train.png")  # 保存图片

# 线性模型可视化
plt.figure("Inference")
plt.title("Linear Regression", fontsize=24)
plt.plot(x_test, y_test, color="red", label="inference")  # 绘制模型线条
plt.scatter(train_data, y_true)  # 原始样本散点图

plt.legend()
plt.grid()  # 绘制网格线
plt.savefig("infer.png")  # 保存图片
plt.show()  # 显示图片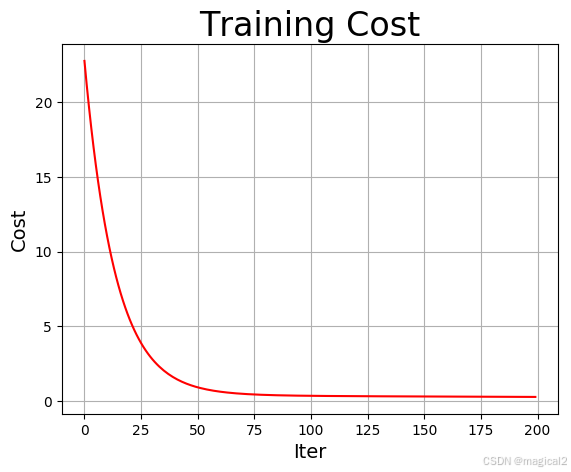

7.完整代码

#线性回归
import numpy as np
import matplotlib.pyplot as plt
import paddle
import paddle.fluid as fluid

#1.准备数据样本
train_data = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]).astype('float32')
y_true = np.array([[5.0], [5.5], [6.0], [6.8], [6.8]]).astype('float32')
#2.定义模型
##定义占位符张量
x=fluid.layers.data(name='x', shape=[1], dtype='float32')
y=fluid.layers.data(name='y', shape=[1], dtype='float32')
y_predict=fluid.layers.fc(input=x,#输入张量
                          size=1,#输出值的个数
                          act=None)
#3.定义损失函数，优化器
cost=fluid.layers.square_error_cost(input=y_predict,#预测值
                                    label=y)#标签值
avg_cost=fluid.layers.mean(cost)#求均值，均方差
optimizer=fluid.optimizer.SGD(learning_rate=0.01)#优化器
optimizer.minimize(avg_cost)#指定优化的目标函数
#4.训练
costs=[]#存储损失值
iters=[]#存储迭代次数
values=[]#存储预测值
params={"x":train_data,"y":y_true}
place=fluid.CPUPlace()
exe = fluid.Executor(place)
exe.run(fluid.default_startup_program())#初始化

for i in range(200):
    outs=exe.run(program=fluid.default_main_program(),
                 feed=params,#参数字典
                 fetch_list=[y_predict,avg_cost])#返回预测值，损失函数的值
    iters.append(i)#存储迭代次数
    costs.append(outs[1][0])#存储损失值
    print("i:",i,"cost:",outs[1][0])#打印损失值
#5.绘图
# 线性模型可视化
tmp = np.random.rand(10, 1)  # 生成10行1列的均匀随机数组
tmp = tmp * 2  # 范围放大到0~2之间
tmp.sort(axis=0)  # 排序
x_test = np.array(tmp).astype("float32")
params = {"x": x_test, "y": x_test}  # y参数不参加计算，只需传一个参数避免报错
y_out = exe.run(feed=params, fetch_list=[y_predict.name])  # 预测
y_test = y_out[0]

# 损失函数可视化
plt.figure("Trainging")
plt.title("Training Cost", fontsize=24)
plt.xlabel("Iter", fontsize=14)
plt.ylabel("Cost", fontsize=14)
plt.plot(iters, costs, color="red", label="Training Cost")  # 绘制损失函数曲线
plt.grid()  # 绘制网格线
plt.savefig("train.png")  # 保存图片

# 线性模型可视化
plt.figure("Inference")
plt.title("Linear Regression", fontsize=24)
plt.plot(x_test, y_test, color="red", label="inference")  # 绘制模型线条
plt.scatter(train_data, y_true)  # 原始样本散点图

plt.legend()
plt.grid()  # 绘制网格线
plt.savefig("infer.png")  # 保存图片
plt.show()  # 显示图片