关于二分图

二分图，又称为二部图、偶图，是一种重要的图模型

二分图判定

下面给出二分图的定义：
给定无向图G = < V,E >，如果可以将结点集V划分成两个子集V1和V2，使得边集E中的任何一条边，一个结点在V1中，另一个在V2中
具备这样性质的图，称为二分图
其中V1和V2称为结点互补集
通常将二分图记为G = < V1,E,V2 >
如果V1 中的每个结点和V2 中的每个结点之间都有边，则称 G = < V1,E,V2 > 为完全二分图

根据二分图的定义，可以得到平凡图和零图都是二分图。同时，由于没有一条边的两个结点同属于V1 或V2 ，因此在二分图中，没有自回路

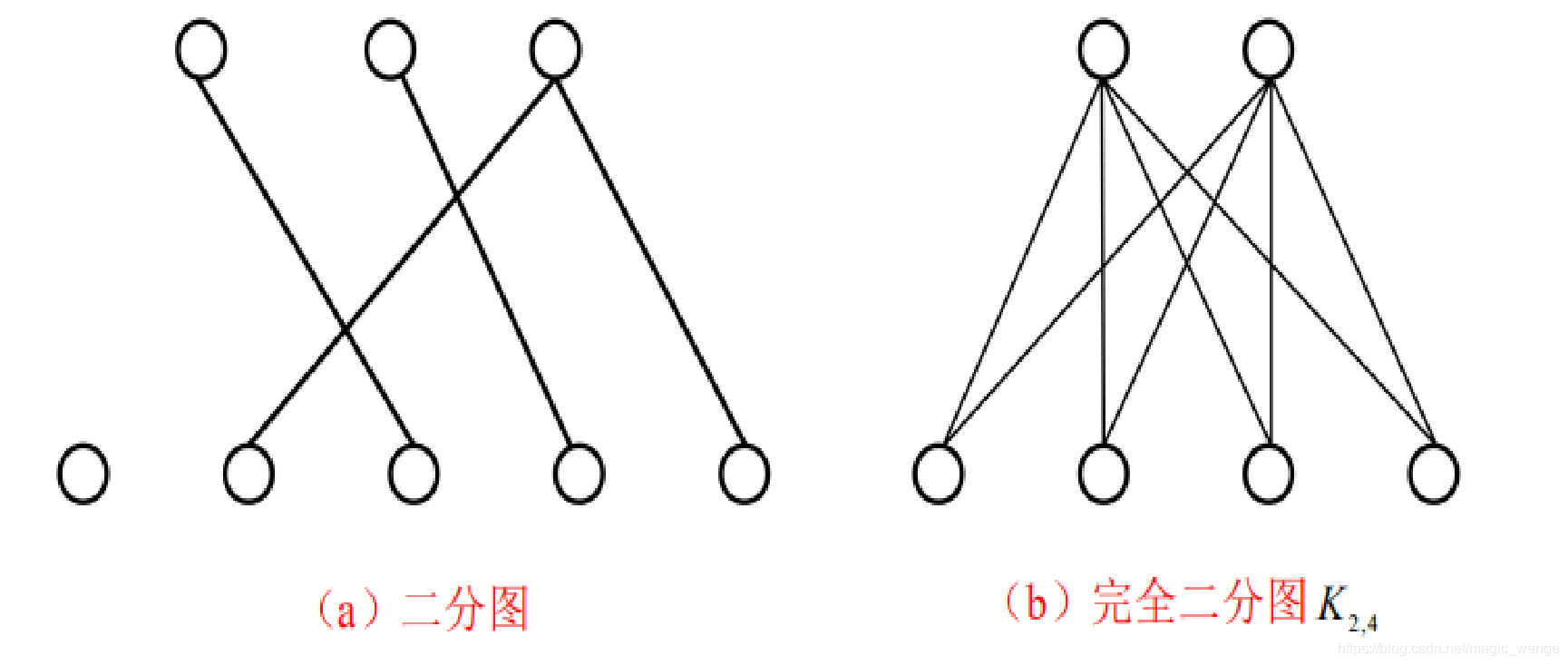
判断一个图是否为二分图的关键在于能否将图的结点集划分为两个结点集，其中两个结点集之间没有边存在

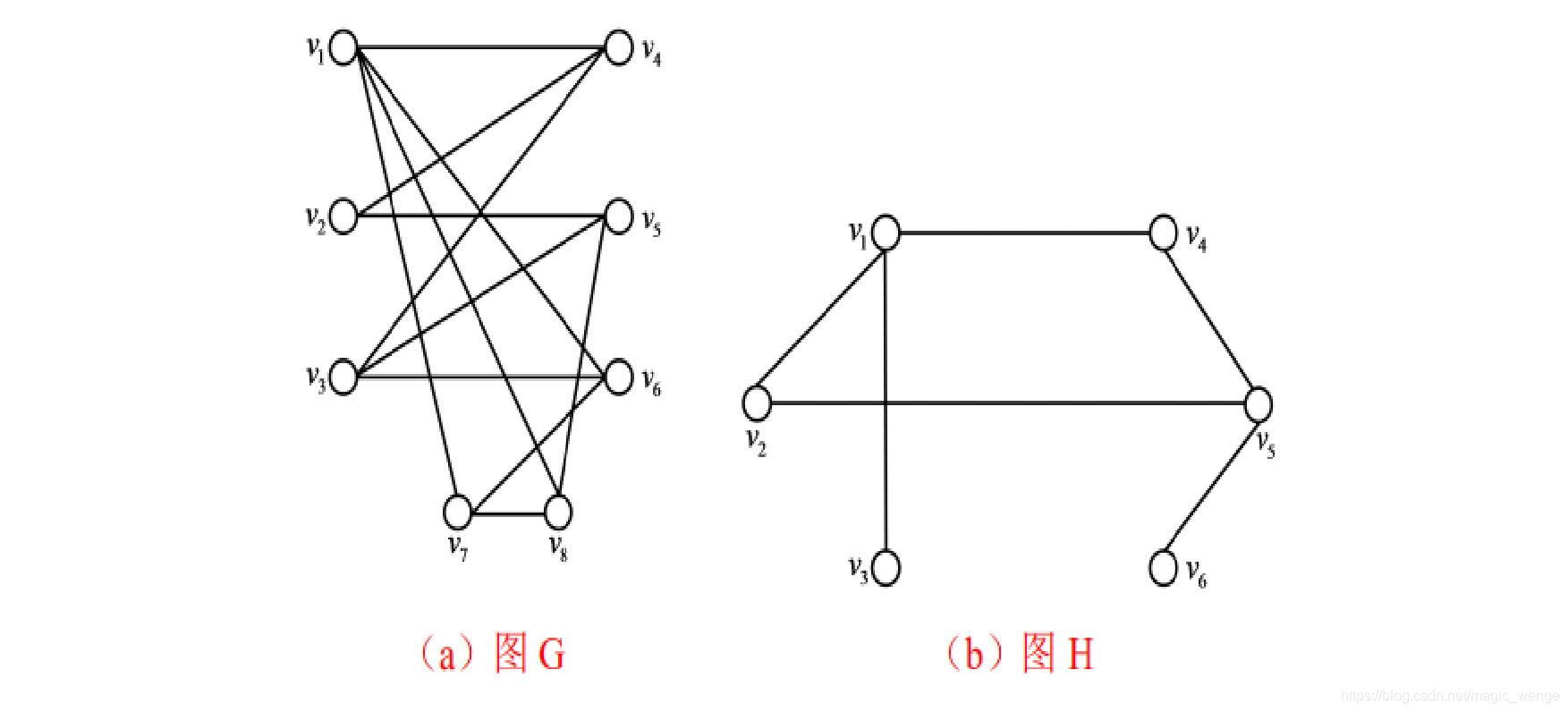
我们把v1放在一个结点集中，与他有边的结点v4，v6，v7，v8应当属于另一个结点集，但是结点v6和v7之间有边，不符合二分图的定义，所以a图不是二分图
同理b图，把v1放在一个结点集中，与他有边的结点v2，v3，v4属于另一个结点集，看v5，v5与v1在一个结点集，其他与他有边的点属于另一个结点集，符合二分图的定义，所以b图是二分图

判定定理
设 G = < V, E > 是无向图，则该图是二分图，当且仅当 G 中所有的回路长度是偶数

我们还可以用图的着色来判断二分图
如果一个无向图只能被两种颜色着上，他的着色数是2的话，那么这个图就是二分图

vector<int>G[1001];
int T,n,m,col[1001];

int dfs(int u,int c)
{
	if(col[u] == 0) col[u] = c;
	for(auto v : G[u]){
		if(col[v] == c) return 0;
		if(col[v] == 0 && dfs(v,-c) == 0) return 0;
	}
	return 1;
}

void Solve(){
	for(int i=1;i<=n;i++){
		if(col[i] == 0){
			if(dfs(i,1) == 0){
				printf("No\n");
				return;
			}
		}
	}
	printf("Yes\n");
}

int main(){
	
	scanf("%d",&T);
	while(T--){

		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++){
			col[i] = 0;
			G[i].clear();
		}
		for(int i=0;i<m;i++){
			int u,v;
			scanf("%d%d",&u,&v);
			G[u].push_back(v);
			G[v].push_back(u);
		}
		Solve();
	}	
	return 0;
}

二分图匹配

给出二分图匹配的定义：
设G = < X, E,Y > 是二分图，X 和 Y 是互补结点子集。若存在 E 的子集 M ，使 M 中的边没有共同结点，称 M 为图 G 的一个匹配。
G 中与 M 中的边相关联的结点称为匹配 M 的饱和结点，其他结点称为非饱和结点。
如果 X 中每个结点都是匹配 M 的饱和结点，则称 M 为 G 的一个 X -完全匹配；如果Y 中每个结点都是匹配 M 的饱和结点，则称 M 为 G 的一个Y -完全匹配
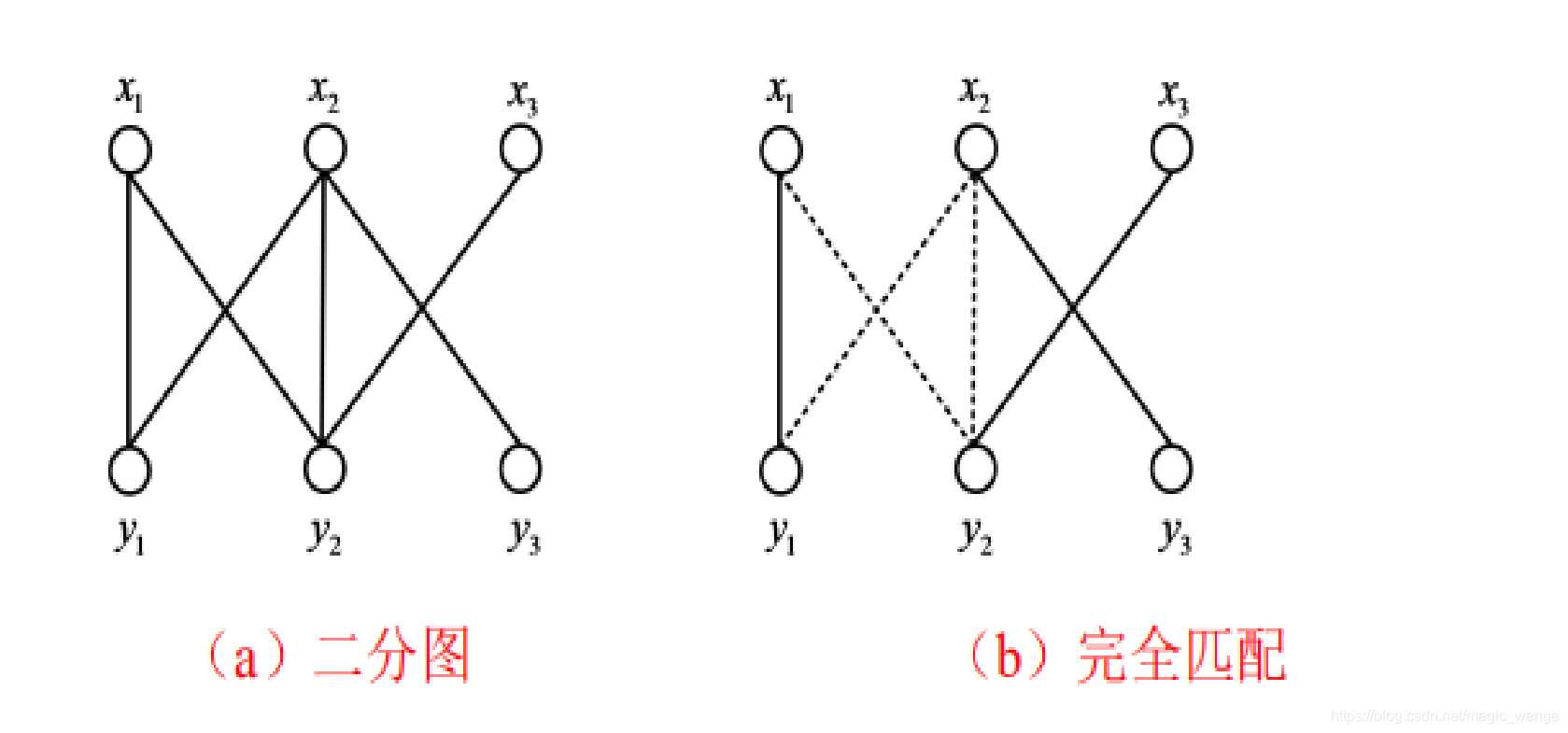
如果 M 既是 X -完全匹配，又是Y -完全匹配，称该匹配为 G 的完全匹配
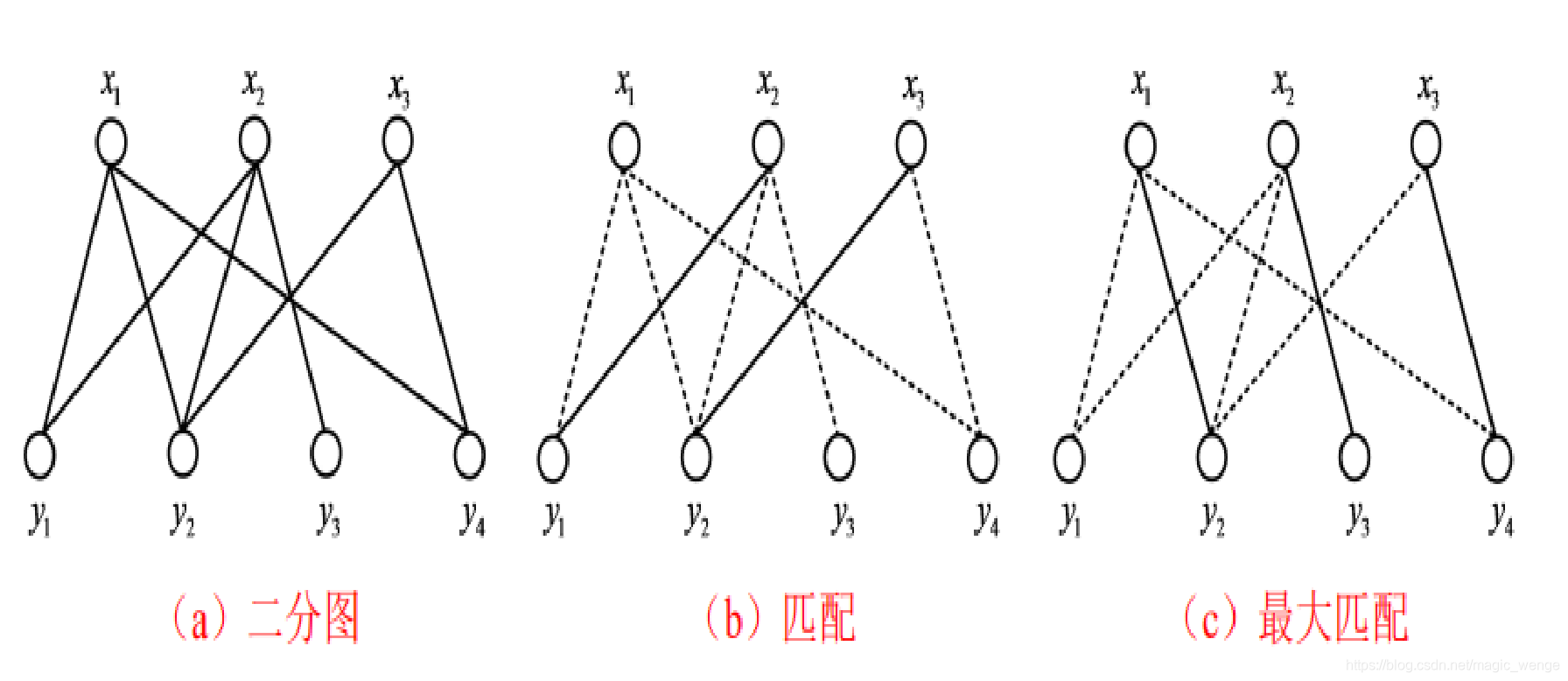
G 中基数最大的匹配称为 G 的最大匹配，最大匹配中边的数量称为 G 的匹配数