妈妈问我的桌子为什么这么乱！

熵是个奇怪的概念。有人说它可以衡量一个物理系统的混乱程度，也有人说这是衡量信息的一种方法，但也有人将它放进蒸汽机的背景中讨论。那么它到底是什么，如何将不同背景中谈到的熵联系起来？

蒸汽机

萨迪·卡诺（1796-1832）

 

让我们从头开始来探究熵的概念。

十九世纪，蒸汽机逐渐兴起，但同时它也暴露了一个严重问题：蒸汽机的能量转化效率极低。

这激发了一位年轻的法国工程师萨迪·卡诺研究热机效率的理论极限（热机的功能是将从热库吸收的热量转化成功，并把剩余热量传递给低温热源）。

1824年，卡诺出版了一本书，书名是《论火的动力》，书中他指出，无论多么完美的热机，效率都不可能达到100%。热机中的能量在传递过程中一定有一部分会被浪费掉。

克劳修斯（1822-1888）

卡诺之后大约四十年，鲁道夫·克劳修斯致力于解决这种不能将热量完全转化成功的问题。他找到了一个数学表达式（见方框）来量化物理系统中无法转化的能量，他把这个量叫做系统的熵。

熵的经典定义

对于可逆的热力学过程，系统向温度为 T 的热源转移数量为 Q 的热量，那么系统中熵的变化ΔS 可以写成：

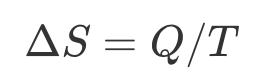
对于可逆系统，系统总熵不变。

无序

卡诺提出了他对热机非常深刻的看法，尽管他认为热是一种流体，但事实并非如此。多亏了克劳修斯、开尔文勋爵和詹姆斯·克拉克·麦克斯韦（以及其他人），我们现在知道，热是一种特殊形式的能量，它起源于构成物质的分子和原子的运动。

这些振动，旋转，或在液体或气体中的随机移动，在运动过程中相互反弹。它们之间的碰撞越剧烈，相应的平均动能就越高，它们所构成的非物质就越热。每当有东西融化时你都能看到。

例如，在一个冰块中，单个分子被限制在一个刚性晶格中，但一旦你加热它，它们就会开始剧烈振动，最终断开与其他水分子之间的连接，使水变得更热，同时融化成液体。

圣诞金字塔：顶部的风扇叶片由蜡烛的热量提供动力。

麦克斯韦、路德维希·玻尔兹曼和其他人后来意识到，熵可以被视为系统无序性的一种度量。如果你想知道这两个概念是怎么连接起来的，那么你可以想象一下一个房间里有一支燃烧的蜡烛。蜡烛的热量可以转化为功。例如，你可以利用从下向上升起的热空气来驱动一个顶部有风扇叶片的圣诞玩具。现在想象一下，蜡烛燃尽后，整个房间的温度是均匀的。这时，整个系统不能再对外做功，所以如果你把熵看作是衡量体系不能做功的能力的量，那么很明显，当蜡烛燃尽时，房间的熵比蜡烛仍在燃烧时要高。

第二种情况中，在分子尺度上来看，随着蜡烛的熄灭系统变得不那么有序了。空气的温度是均匀的，这意味着快分子和慢分子是完全混合在一起的：如果它们以某种方式被分离出来，那么在房间里中就会出现一个温度梯度。实际上，房间所处的热平衡也是最大无序状态。相比之下，当蜡烛还在燃烧时，快速分子会聚集在火焰周围，使情况表现得更加有序。

 

麦克斯韦和玻尔兹曼提出了一个公式用以计算由许多成分组成的系统（如气体）中的无序程度。这个公式基于以下观点：系统有序性越低，系统的同一个宏观状态对应的微观状态越多。结果表明，用无序性定义的熵和克劳修斯用温度与热量定义的熵是等价的。

熵的微观定义

‍‍假设气体处于某种特殊的宏观状态，例如，拥有特定的温度和压强。W 是满足这种宏观状态的微观状态的个数，熵 S 可以定义为：

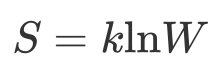
其中 k 是玻尔兹曼常数:

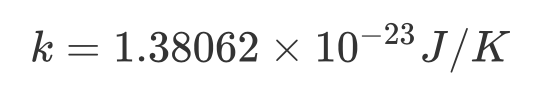
J 是能量单位焦耳, K 是温度单位开尔文.这行公式刻在玻尔兹曼位于维也纳的墓碑上。

以上公式用于所有分子出现概率相同的情形中。当出现概率不同时，可以用下面这个更普适的公式：

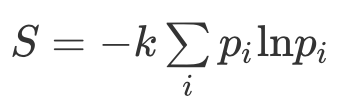
p_i是第 i 个组分出现的概率。

玻尔兹曼的墓碑

信息

那么熵是怎么和信息联系到一起的？

如果一个系统是非常有序的，那么你不需要太多的信息来描述它。例如，你可以用一句话来描述冰冻冰块中分子的规则排列，但是要精确描述气体，气体中的分子随机地飞来飞去，你需要知道每个分子的精确位置和速度才能完全描述整个系统，这需要很多信息。无序越多，熵越高，描述系统所需的信息就越多。

这就是熵的概念如何将发动机的效率与无序以及信息联系起来。

熵也包含在自然的一个基本定律中：热力学第二定律说，孤立系统的熵永远不会减少。它只能保持不变或增加。就发动机而言，这意味着任何发动机永远不会自动提高自己的效率，这也很符合直觉。就有序性而言，这意味着任何系统只会变得更加混乱，这也符合直觉（想想你的厨房或办公桌）。正如我们所看到的，混乱的事物比有序的事物更难描述，这就从信息角度给出了对热力学第二定律理解。

作者：Marianne

翻译：Nothing

审校：Nuor

原文链接：

https://plus.maths.org/content/maths-minute-entropy

我们是谁：MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！
扫描二维码关注更多精彩《猫和老鼠》里的魔术艺术（四）——夸张与对比

扔硬币中的思考——隐含变量建模魔术里的集合、映射和关系（十）——天才之作《Tiny Berglas Effect》我和Double Lift的故事（五）——升华篇
闯红灯到底该不该罚款？——逻辑推理浅谈（二）点击阅读原文，往期精彩不错过!