背景
最近,西安大唐不夜城“不倒翁”女孩街头表演的视频走红网络。在大唐不夜城步行街,“不倒翁”小姐姐身姿轻盈眼神妩媚令人梦回大唐,一颦一笑将中国唐朝美人的妩媚娇羞演绎得淋漓尽致(这段话网上抄来的,大模头觉“身姿轻盈”不适合以胖为美的大唐女性)。
这勾人的小眼神,大模头看了觉得画面太美还能看 100 遍。要不是大模头心中早有相中的小妖,哪轮到这些游客拉手啊。

尽管很美,但小姐姐一定表演得很辛苦。扮演不倒翁的演员冯佳晨,今年23岁。虽有近10年的舞蹈功底,但这个节目刚开始的时候对她来说真的不容易。因表演需要将下半身完全固定在铁架子上,仅靠腰部发力运作不倒翁的底座,冯佳晨每天表演完胯和膝盖都会被磨青。

问题
大模头从小就玩过不倒翁,还用鸡蛋壳做过不倒翁。一直很好奇,不倒翁为什么不倒?

原理并不难以理解:上轻下重的物体比较稳定,也就是说重心越低越稳定。当不倒翁在竖立状态处于平衡时,重心和接触点的距离最小,即重心最低。偏离平衡位置后,重心总是升高的。因此,这种状态的平衡是稳定平衡。所以不倒翁无论如何摇摆,总是不倒的。但不倒翁究竟是如何运动的呢?
模型
不倒翁一般都是上半身重量很轻,下半身是一个实心的半球体,重量较大, 不倒翁的重心就在半球体之内。为了简化问题,我们先不考虑小姐姐,把不倒翁简化为仅在二维平面(图 1 中的 平面)内运动的半球。先确定半球的质心和转动惯量,然后再求解运动方程。
考虑如图 1 所示的半球,其质量为 ,质心为 ,半球球心为 。
容易求得半球质心位置 和对 轴的转动惯量[1]
为简化问题,仅考虑半球在 平面内运动。若该半球某时刻的位置如图 2 所示, 为半球重力,地面对半球的支撑力和摩擦力分别为 和 。
为了确定运动方程,需要知道半球是如何运动的。我们用 与垂直方向的角度变量 来描述半球的状态。考虑点 、 和 的速度
其中 和 是 和 对时间的一阶导数。将 点速度对时间求导数,得到质心的加速度
接下来,我们通过考虑作用在物体上的所有力来研究运动方程。运动方程不仅要考虑刚体的平动,还必须考虑到关于质心的转动:
三个方程,却有四个未知数(,,,)。要求解这个问题,还需要一个描述接触条件的表达式。对于不倒翁,假设半球与地面接触点没有滑移,则有
或
从而可得:
半球球心 点的位置(公式有误,2 应改为 π):
仿真
经过大模头的分析,终于得到了小姐姐的摇晃方程。可小淫魔小烎(yín)模说看不懂方程,小烎模不想看方程,就要看小姐姐摇。没办法,为了满足一下小烎模的欲望,大模头只好写段 MATLAB 程序模拟一下。假设底座半圆半径 m,质量 kg,初始角度为 ,模拟步长 s。模拟的主要步骤如下:
-
根据角速度更新角度:
-
根据角加速更新角速度:,其中角加速度 由运动方程给出。
-
确定半圆圆心 的水平位置:。
-
根据半圆圆心 的水平位置,以及半圆的转动角度,确定半圆位置。
-
更新时间 。如果 晚上,结束,否则跳到第 1 步。
为了模拟的视觉效果,大模头还需要动态展示出结果。首先需要画一个半圆和一个性感的小姐姐:
%% 画半圆r = 0.5; % [m] 半径Xb = r*cosd(180:360);Yb = r*sind(180:360);hb = fill(Xb,Yb,[1,0.8,0.8]);hold on%% 画小姐姐x = [0.0 0.2 0.2 0.2 0.0 -0.2 -0.3 -0.6 ... 0.1 0.1 0.1 0.0 -0.1 -0.1 -0.1 NaN];y = [1.6 0.8 1.1 1.4 1.4 1.4 1.2 1.2 ... 0.0 0.5 0.9 1.0 0.9 0.5 0.0 NaN];I = [1 5 12 16 2 3 4 5 6 7 8 16 9 10 11 12 13 14 15];Xm = x(I); Ym = y(I);hm = plot(Xm, Ym,'bo-');
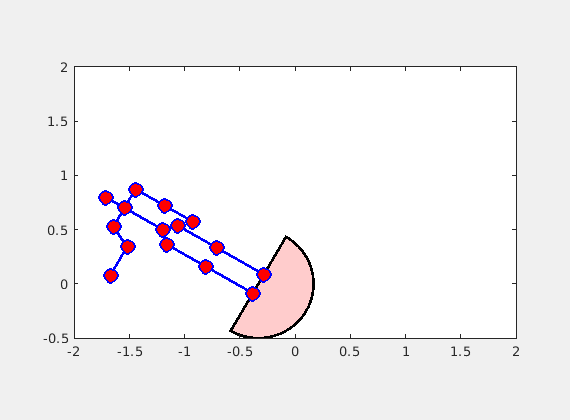
绘制结果如图 3 所示。小烎模看了我画的小姐姐,表示震惊:十再是太像了,将小姐姐妙曼的身姿展现得淋漓尽致,这大长腿,这伸出的纤纤玉手 。。。
根据运动方程,算出某时刻半圆心的位移以及角度后,需要对半圆和小姐姐进行平移和旋转。平移容易,旋转可根据以下公式进行
将以上公式写成 MATLAB 函数:
function [x, y] = rotxy(x0, y0, theta)% 将 (x0,y0) 绕 (0,0) 旋转 -theta 度x = x0*cosd(theta) + y0*sind(theta);y = -x0*sind(theta) + y0*cosd(theta);end
更多模拟细节见文末附录中的 MATLAB 完整代码。模拟结果见图 4。小烎模非常满足地看了一晚上。
结论
-
尽管不倒翁的原理并不难,但大唐不夜城“不倒翁”小姐姐摇一晚上也肯定很累,为“不倒翁”女孩点赞!
-
通过运动和受力分析建立数模模型可以求解出不倒翁的运动方程。
-
通过对运动方程的数值积分,可以模拟出不倒翁运动。感兴趣的同学可以做个三维模拟,如果有想法,可以联系大模头。
附录
%% 微信公众号:数学模型(MATHmodels)%% 底座半球数据r = 0.5; % [m] 半径m = 300; % [kg] 质量g = 9.8; % [m/s] 重力加速度h = 3/8*r; % [m] 重心位置Ic = 83/320*m*r^2; % [kg*m^2] 转动惯量theta = -60; % [deg] 初始角度omega = 0; % [deg/s] 初始角速度xo = pi*theta/180*r; % [m] 初始位移dt = 5e-2; % [s] 仿真步长
%% 画半球(半圆)Xb = r*cosd(180:360);Yb = r*sind(180:360);[xb, yb] = rotxy(Xb,Yb,theta);hb = fill(xb+xo,yb,[1,0.8,0.8]);hold on; axis imageaxis([-2,2,-0.5,2]);
%% 画小姐姐x = [0.0 0.2 0.2 0.2 0.0 -0.2 -0.3 -0.6 ... 0.1 0.1 0.1 0.0 -0.1 -0.1 -0.1 NaN];y = [1.6 0.8 1.1 1.4 1.4 1.4 1.2 1.2 ... 0.0 0.5 0.9 1.0 0.9 0.5 0.0 NaN];I = [1 5 12 16 2 3 4 5 6 7 8 16 9 10 11 12 13 14 15];Xm = x(I); Ym = y(I);[xm, ym] = rotxy(Xm,Ym,theta);hm = plot(xm+xo,ym,'bo-','MarkerFaceColor',[1,0,0]);
%% 让小姐姐摇一晚上for t = 0:dt:3600*12 % 更新角度 theta = theta + omega * dt; % 更新解加速度 omega = omega - h*m*(g+r*omega)*sind(theta) ... / (Ic+m*(r^2+h^2-2*h*r*cos(theta)))*dt; % 更新中心位移 xo = 2*theta/180 * r;
% 根据角度旋转座标点 [xb, yb] = rotxy(Xb, Yb, theta); [xm, ym] = rotxy(Xm, Ym, theta);
% 更新图形并显示 set(hb, 'XData',xb+xo, 'YData',yb) set(hm, 'XData',xm+xo, 'YData',ym) drawnowend
% ------------------------------------------------
function [x, y] = rotxy(x0, y0, theta)% 将 (x0,y0) 绕 (0,0) 旋转 -theta 度x = x0*cosd(theta) + y0*sind(theta);y = -x0*sind(theta) + y0*cosd(theta);end
参考资料
[1]
Mass moment of inertia of a hemisphere: https://blitiri.blogspot.com/2014/05/mass-moment-of-inertia-of-hemisphere.html
[2]
How to determine the axis of rotation of a rigid body?: https://physics.stackexchange.com/questions/372853/how-to-determine-the-axis-of-rotation-of-a-rigid-body
关注更多精彩
听说程序员又把妹子谈飞了?——逻辑推理浅谈(一)
循环、递归与魔术(五)——再谈递归的魔术逻辑与欣赏
Roberto Giobbi的纸牌大学
我的亲子魔术首秀
Michael Ammar 来了!




















 1588
1588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








