高斯混合模型（GMM）

1. 前言

高斯混合模型是使用高斯分布对原始数据进行估计，其中高斯函数的均值$\mu$和方差$\sigma$以及各个高斯函数分量占的比例$\alpha$这些参数是未知的。对于它们的求解是通过EM算法实现的。
高斯混合模型可以表述为如下的概率分布模型：
$$P(y|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (y|{\theta }_k)$$
其中，${\alpha }_k$是系数，${\alpha }_k\ge 0$，${\sum }_{k=1}^K{\alpha }_k=1$；$\varphi (y|{\theta }_k)$是高斯分布密度，${\theta }_k=({\mu }_k,{\sigma }_k^2)$
$$\varphi (y|{\theta }_k)=\frac{1}{\sqrt{2\pi }{\sigma }_k}exp(-\frac{(y-{\mu }_k{)}^2}{2{\sigma }_k^2})$$
称为第K个分模型。

2. 推导

2.1 确定隐藏参数

假设观测数据$y_1,y_2,\dots ,y_N$是由高斯混合模型生成
$$P(y|\theta )=\sum _{k=1}^K{\alpha }_k\varphi (y|{\theta }_k)$$
其中，参数$\theta =({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k;{\theta }_1,{\theta }_2,\dots ,{\theta }_k)$。是高斯混合模型中直观需要求解的未知变量。但是高斯混合模型中就只有这两类变量是未知的么？
对于观测数据$y_j$，$j=1,2,\dots ,N$，是这样产生的：首先依据概率${\alpha }_k$选择第$k$个高斯分布模型$\varphi (y|{\theta }_k)$；然后依据第$k$个分模型的概率分布$\varphi (y|{\theta }_k)$生成观测数据$y_j$。这个时候观测数据$y_j$，$j=1,2,\dots ,N$，是已知的；但是呢，反映观测数据$y_j$具体是来自第$k$个分模型的数据是未知的。$k=1,2,\dots ,K$，这里以隐变量${\gamma }_{jk}$表示，可以将其定义为：
$${\gamma }_{jk}=\{\begin{array}{ll}1,& \text{第j个观测数据来自第k个分模型}\\ 0,& \text{否则}\end{array}$$
其中，$j=1,2,\dots ,N;k=1,2,\dots ,K$，显然${\gamma }_{jk}$是属于典型的0-1随机变量。因而完整的观测数据就可以写为：
$$(y_j,{\gamma }_{j1},{\gamma }_{j2},\dots ,{\gamma }_{jK}),j=1,2,\dots ,N$$

2.2 得到似然函数，确定Q函数

于是，可以写出完全数据的似然函数：
$$\begin{array}{rl}P(y,\gamma |\theta )& =\prod _{j=1}^{N}P(y_j,{\gamma }_{j1},{\gamma }_{j2},\dots ,{\gamma }_{jK})\\ & =\prod _{j=1}^N\prod _{k=1}^K[{\alpha }_k\varphi (y_j|{\theta }_k){]}^{{\gamma }_{jk}}\\ & =\prod _{k=1}^K{\alpha }_k^{n_k}\prod _{j=1}^N[\varphi (y_j|{\theta }_k){]}^{{\gamma }_{jk}}\\ & =\prod _{k=1}^K{\alpha }_k^{n_k}\prod _{j=1}^N[\frac{1}{\sqrt{2\pi }{\sigma }_k}exp(-\frac{(y-{\mu }_k{)}^2}{2{\sigma }_k^2}){]}^{{\gamma }_{jk}}\end{array}$$
其中，$n_k={\sum }_{j=1}^N{\gamma }_{jk}$，$N={\sum }_{k=1}^K{n}_k$
因而，完全数据的对数似然函数为：
logP(y,γ∣θ)=∑k=1K{nklogαk+∑j=1Nγjk[log(12π)−logαk−12π(yj−μk)2]}logP(y,\gamma|\theta)=\sum_{k=1}^K \{n_klog\alpha_k+\sum_{j=1}^N\gamma_{jk}[log(\frac{1}{\sqrt{2\pi}})-log\alpha_k-\frac{1}{\sqrt{2\pi}}(y_j-\mu_k)^2]\}logP(y,γ∣θ)=k=1∑K​{nk​logαk​+j=1∑N​γjk​[log(2π​1​)−logαk​−2π​1​(yj​−μk​)2]}
在上面得到了完全数据的对数似然函数，接下来就需要使用EM算法求解模型中的未知参数了。首先是EM算法的E步，也就是求解期望，得到Q函数。
Q(θ,θ(i))=E[logP(y,γ∣θ)∣y,θ(i)]=E{∑k=1K{nklogαk+∑j=1Nγjk[log(12π)−logαk−12π(yj−μk)2]}}=∑k=1K{∑j=1N(Eγjk)logαk+∑j=1N(Eγjk)[log(12π)−logαk−12π(yj−μk)2]} \begin{aligned} Q(\theta,\theta^{(i)}) & = E[logP(y,\gamma|\theta)|y,\theta^{(i)}]\\ & = E\{\sum_{k=1}^K \{n_klog\alpha_k+\sum_{j=1}^N\gamma_{jk}[log(\frac{1}{\sqrt{2\pi}})-log\alpha_k-\frac{1}{\sqrt{2\pi}}(y_j-\mu_k)^2]\}\}\\ & =\sum_{k=1}^K \{\sum_{j=1}^N(E\gamma_{jk})log\alpha_k+\sum_{j=1}^N(E\gamma_{jk})[log(\frac{1}{\sqrt{2\pi}})-log\alpha_k-\frac{1}{\sqrt{2\pi}}(y_j-\mu_k)^2]\} \\ \end{aligned} Q(θ,θ(i))​=E[logP(y,γ∣θ)∣y,θ(i)]=E{k=1∑K​{nk​logαk​+j=1∑N​γjk​[log(2π​1​)−logαk​−2π​1​(yj​−μk​)2]}}=k=1∑K​{j=1∑N​(Eγjk​)logαk​+j=1∑N​(Eγjk​)[log(2π​1​)−logαk​−2π​1​(yj​−μk​)2]}​
这里记$\widehat{{\gamma }_{jk}}=E({\gamma }_{jk}|y,\theta )$，则：
$$\widehat{{\gamma }_{jk}}=\frac{{\alpha }_k\varphi (y_j|{\theta }_k)}{{\sum }_{k=1}^K{\alpha }_k\varphi (y_j|{\theta }_k)}$$
$\widehat{{\gamma }_{jk}}$是在当前模型参数下第$j$个观测数据来自第$k$个分模型的概率，成为分模型k对观测数据$y_j$的响应度。
将$\widehat{{\gamma }_{jk}}=E{\gamma }_{jk}$及$n_k={\sum }_{k=1}^{N}E{\gamma }_{jk}$，可得：
Q(θ,θ(i))=∑k=1K{nklogαk+∑j=1Nγjk^[log(12π)−logαk−12π(yj−μk)2]}Q(\theta,\theta^{(i)})=\sum_{k=1}^K \{n_klog\alpha_k+\sum_{j=1}^N\hat{\gamma_{jk}}[log(\frac{1}{\sqrt{2\pi}})-log\alpha_k-\frac{1}{\sqrt{2\pi}}(y_j-\mu_k)^2]\}Q(θ,θ(i))=k=1∑K​{nk​logαk​+j=1∑N​γjk​^​[log(2π​1​)−logαk​−2π​1​(yj​−μk​)2]}

2.3 EM算法M步

之后，便是使用EM算法的M步求$Q(\theta ,{\theta }^{(i)})$对$\theta$的极大值，即求新一轮迭代的模型参数
$${\theta }^{i+1}=arg\underset{\theta }{\max }Q(\theta ,{\theta }^{(i)})$$
这里用$\widehat{{\mu }_k},\widehat{{\sigma }_k^2},\widehat{{\alpha }_k}$来表示${\theta }^{i+1}$中的各参数。对于参数$\widehat{{\mu }_k},\widehat{{\sigma }_k^2}$可以通过上述的Q函数对应求导取极值得到；对于$\widehat{{\alpha }_k}$是在${\sum }_{k=1}^K=1$条件下求偏导数并令其为0得到。因而可以得到如下的参数更新公式

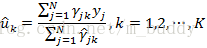
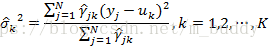
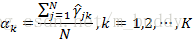
3. 高斯混合模型参数估计的EM算法

输入：观测数据$y_1,y_2,\dots ,y_N$，高斯混合模型
输出：高斯混合模型中的参数
step1：取参数的初始值开始迭代
step2：E步，依据当前模型的参数，计算分模型$k$对观测数据$y_j$的响应度
$$\widehat{{\gamma }_{jk}}=\frac{{\alpha }_k\varphi (y_j|{\theta }_k)}{{\sum }_{k=1}^K{\alpha }_k\varphi (y_j|{\theta }_k)}$$
step3：M步，计算新一轮迭代的模型参数



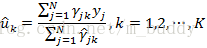
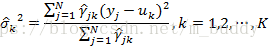
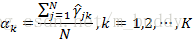
step4：重复step2和step3，直到收敛。

后记：本篇博客主要讲了高斯混合模型的推导以及演算的过程，没有讲解相关的实用例子，在后面的博客中将会讲到使用高斯混合模型实现自动化肿瘤分割的任务。这里将其记录下来，留作后用。