《Rethinking Efficient Lane Detection via Curve Modeling》论文笔记

参考代码：pytorch-auto-drive

1. 概述

介绍：在这篇文章中对车道线建模表示进行了讨论和分析，文中指出现有的车道线检测方法大体为：segmentation-based、key_points-based、polynomial-based，当然还有一些其它类型的车道线建模表述方法。在此基础上依靠文章对车道线使用曲线描述函数对车道线进行建模，这样就省去了很多特征解码的相关问题，只需要网络去预测对应曲线的参数就行了。但是在polynomial-based方法中其多项式回归对网络来讲是较难，导致的结果就是其性能相比前面提到的两种类型有较大的差距。对此文章借鉴贝塞尔曲线的描述方式，通过预测3阶贝塞尔曲线描述车道线（通过少量的控制点便可实现曲线描述），并且对特征图进行水平折半反转加可变形卷积的方式实现特征融合和表达能力提升（是来源于场景中车道线相对车中轴是对称分布的）。

上述提到的4中对与车道线的描述见下图所示：

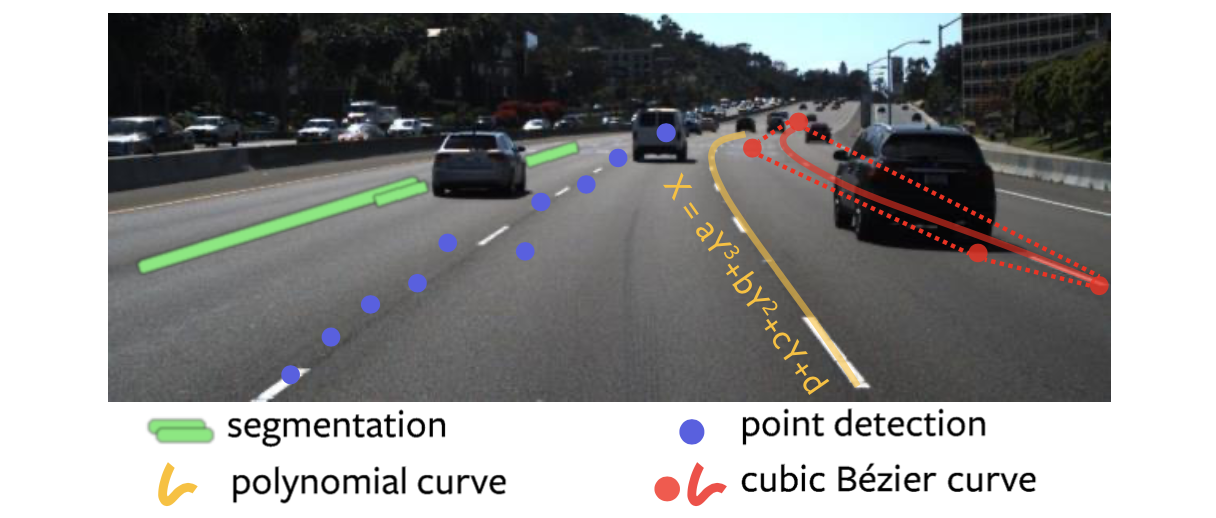
这里文章的车道线是通过预测贝塞尔曲线控制点的方式实现的，然后对应文章的代码实现发现其在对应数据集下车道线的数量是固定的，那么对于自动驾驶场景车道变化复杂的情况，其适应性可能会存在一些问题，这里表示存疑。

PS：关于贝塞尔曲线的相关原理基础可以参考如下资料：
贝塞尔曲线原理(简单阐述)

2. 方法设计

2.1 网络pipeline

文章的整体pipeline见下图所示：

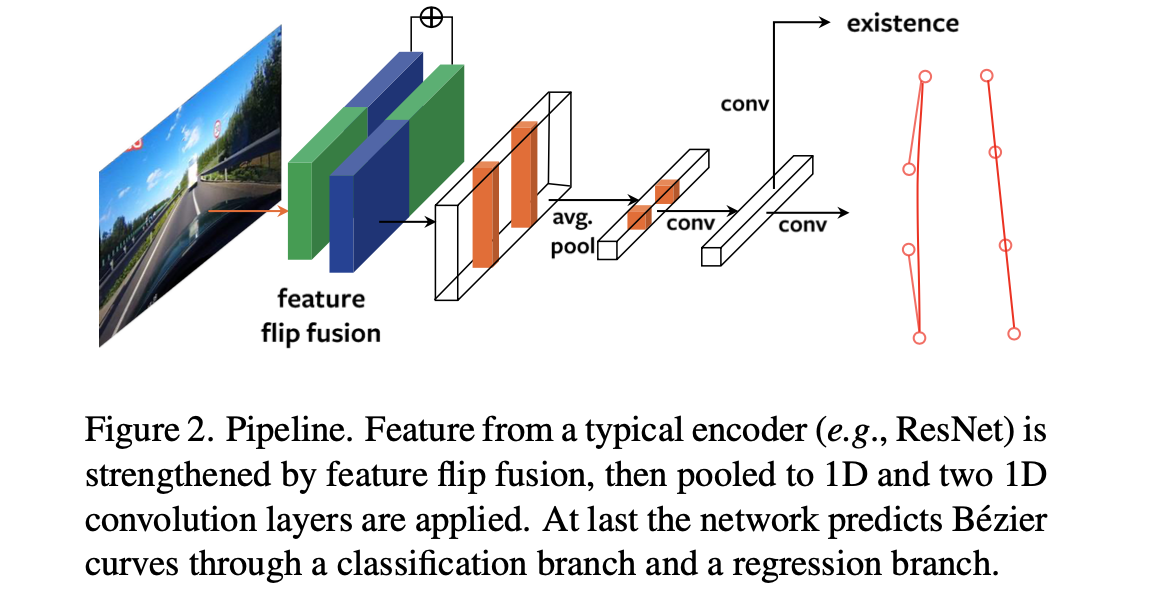
在上图中可以看到其包含了文章所提出的两个创新点：feature flip特征融合与贝塞尔曲线拟合头。

2.2 Feature Flip

这部分是用于特征图感知能力增广的，其是对特征图进行水平折半翻转，之后通过可变形卷积实现特征的增强表达，其网络结构见下图所示：

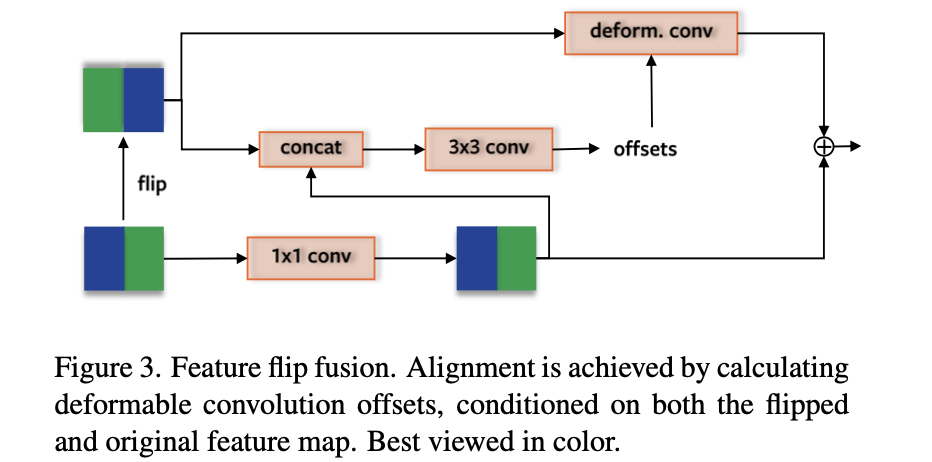
该网络结构的思想是来自于对下图中实际数据的观察，其思想是通过对称原理弥补左右图像区域车道线不明显而导致的检测问题。个人感觉这样的假设先验有一定的道理但是其假设性比较强。

2.3 贝塞尔曲线拟合

曲线的描述：
贝塞尔曲线是控制点和偏置项决定的，则一条曲线可以被描述为：
$$\mathcal{B}=\sum _{i=0}^n{b}_{i,n}(t){\mathcal{P}}_i,0\le t\le 1$$
其中，生成曲线上每一个点的偏移项在阶数$n$（文章中将其设置为3）下的描述为：
$$b_{i,n}=C_n^i{t}^i(1-t{)}^{n-i},i=0,\dots ,n$$

贝塞尔曲线GT生成：
在原始的标注文件中给出的是描述车道线的点坐标，因而需要将这些数据转换到由贝塞尔曲线控制的参数下表达，对此文章是通过最小二乘法的方式计算白塞尔线的GT。

曲线回归匹配与损失函数：
在之前的一些工作中通过L1损失函数的形式去监督贝塞尔曲线的控制点，如下图的（a）图所示，但是这样的结果是由控制点生成的曲线效果并不与实际曲线贴合效果直接关联。对此文章参考polynomial-based中的策略（图c），通过sample采样（文中取采样点为100）的方式去计算曲线的贴合程度。

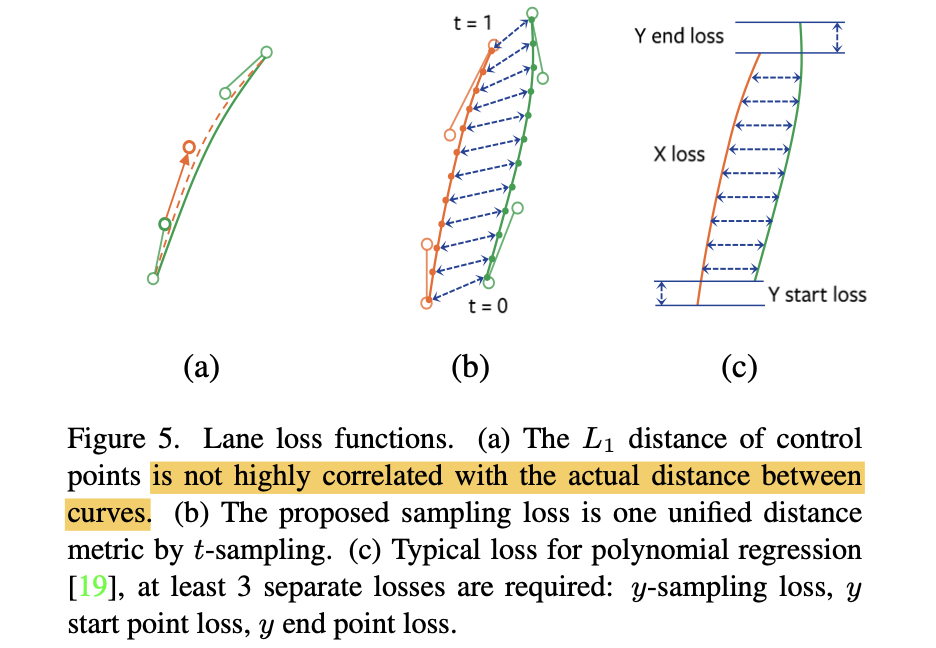
那么对于文章中提到的曲线采样点匹配策略是通过枚举的形式得到的，其描述为：
$$\hat{\pi }=\underset{\pi \in {\prod }_G^N}{\mathrm{argmax}}\sum _i^G{Q}_{i,\pi }(i)$$
其中，$N,G$代表的是采样的点集和GT点集，$\pi (i)$代表的是第$i$车道线。那么匹配的度量是：
$$Q_{i,\pi }(i)=({\hat{p}}_{\pi (i)}{)}^{1-\alpha }\cdot (1-L_1(b_i,{\hat{b}}_{\pi (i)}){)}^{\alpha }$$
其中，${\hat{p}}_{\pi (i)}$代表的是第$i$车道线的分类概率，且$\alpha =0.8$。$L_1(b_i,{\hat{b}}_{\pi (i)})$代表的是对应采样点的差异，可参考上图b中的关联虚线。

损失函数：
首先，对于贝塞尔曲线的整体约束是使用L1的形式：
$$L_{reg}=\frac{1}{n}\sum _{t\in T}||\mathcal{B}(f(t))-\hat{\mathcal{B}}(f(t))|{|}_1$$
对于车道线的分类使用的是加权的二值交叉熵的形式，此外还添加车道线二值分割损失，则整体的损失函数描述为：
$$L={\lambda }_1{L}_{reg}+{\lambda }_2{L}_{cls}+{\lambda }_3{L}_{seg}$$
其中，${\lambda }_1=1,{\lambda }_2=0.1,{\lambda }_3=0.75$。

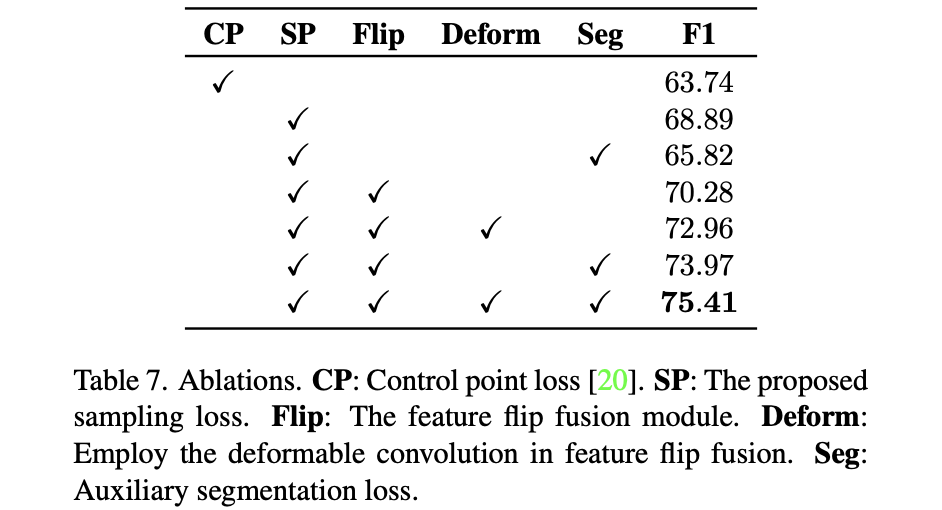
2.4 消融实验

上述2.3节中各分量对整体性能的影响：

3. 实验结果

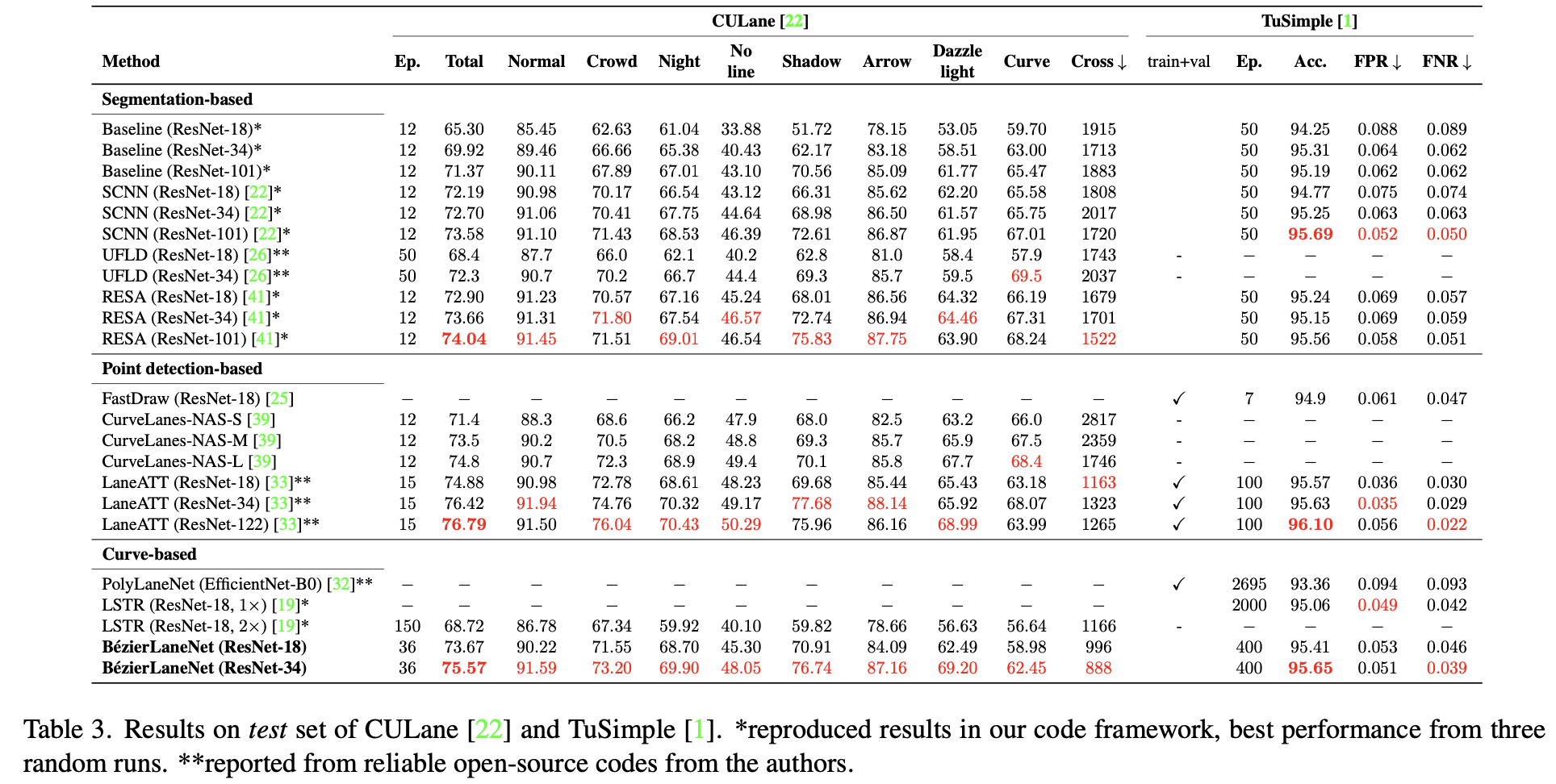
CULane数据集性能比较：