本文详细介绍了如何使用Java实现二叉树的各种遍历方式，包括前序、中序、后序以及广度优先遍历，还涉及到了广度优先遍历的变体、二叉树深度计算、特定路径和判断等。此外，还讲解了如何进行二叉树的合并、镜像操作，以及如何判断二叉树是否为二叉搜索树、完全二叉树或平衡二叉树，最后讨论了如何根据序列重建二叉树。
前序、中序、后续遍历
前序遍历也就是 根左右
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型一维数组
*/
public int[] preorderTraversal (TreeNode root) {
// write code here
List<Integer> list = new ArrayList<Integer>();
solve(list, root);
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++)
res[i] = list.get(i);
return res;
}
// 前序遍历
public void solve(List<Integer> list, TreeNode root) {
if (root == null) return;
list.add(root.val);
solve(list, root.left);
solve(list, root.right);
}
// 中序遍历， 左右根
private void doInorderTraversal(List<Integer> list, TreeNode root) {
if (root == null) return ;
doInorderTraversal(list, root.left);
list.add(root.val);
doInorderTraversal(list, root.right);
}
// 后续遍历
private void doPostorderTraversal(List<Integer> list, TreeNode root) {
if(root == null) return;
doPostorderTraversal(list, root.left);
doPostorderTraversal(list, root.right);
list.add(root.val);
}
}
非递归方式实现前序、中序、后序遍历
- 前序， 根左右
public int[] preorderTraversal (TreeNode root) {
// write code here
if(root == null ) return new int[0];
List<Integer> list = new ArrayList<Integer>();
Stack<TreeNode> s = new Stack<TreeNode>();
s.push(root);
while(!s.isEmpty()) {
TreeNode node = s.pop();
list.add(node.val);
if(node.right != null) {
s.push(node.right);
}
if(node.left != null) {
s.push(node.left);
}
}
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++)
res[i] = list.get(i);
return res;
}
- 中序， 左根右
public int[] inorderTraversal (TreeNode root) {
// write code here
List<Integer> list = new ArrayList<Integer>();
if(root == null) return new int[0];
// doInorderTraversal(list, root);
Stack<TreeNode> s = new Stack<TreeNode>();
while(root != null || !s.isEmpty()) {
// 找到最左边节点
while(root != null) {
s.push(root);
root = root.left;
}
// 访问该节点
TreeNode node = s.pop();
list.add(node.val);
// 进入右节点
root = node.right;
}
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++)
res[i] = list.get(i);
return res;
}
- 后序遍历- 左右根
既然前序，中序都可以使用栈来实现遍历，那么后序肯定也行。只不过比较麻烦一些
public int[] postorderTraversal (TreeNode root) {
// write code here
if(root == null) return new int[0];
List<Integer> list = new ArrayList<Integer>();
Stack<TreeNode> s = new Stack<TreeNode>();
TreeNode pre = null;
while(root != null || !s.isEmpty()) {
while(root != null) {
s.push(root);
root = root.left;
}
TreeNode node = s.pop();
// 如果该节点右节点无，或者已经被访问过
if(node.right == null || node.right == pre) {
//访问该节点
list.add(node.val);
pre = node;
} else {
// 该节点恢复入栈
s.push(node);
// 先访问右边子树
root = node.right;
}
}
int [] res = new int[list.size()];
for(int i =0;i<list.size();i++) {
res[i] = list.get(i);
}
return res;
}
广度优先遍历
使用循环方式，非递归(推荐)
利用队列的先进先出的特征，每次遍历节点时将左右叶子入队；
注意需要每一层单独输出一行，所以在每一层时单独用小循环遍历，遍历的节点数为当前queue的size。
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* }
*/
public class Solution {
/**
*
* @param root TreeNode类
* @return int整型ArrayList<ArrayList<>>
*/
public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
// write code here
Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
if(root == null) return res;
queue.add(root);
while(!queue.isEmpty()) {
ArrayList<Integer> list = new ArrayList<Integer>();
int size = queue.size();
for(int i =0;i<size;i++) {
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(list);
}
return res;
}
}
使用递归方式
这种方式，并不是一层一层地完整输出的，而是先左完了之后再右，只不过带上了深度信息，将对应层的信息放到了二维数组对应行去了。
import java.util.*;
public class Solution {
//记录输出
ArrayList<ArrayList<Integer> > res = new ArrayList();
void traverse(TreeNode root, int depth) {
if(root != null){
//新的一层
if(res.size() < depth){
ArrayList<Integer> row = new ArrayList();
res.add(row);
row.add(root.val);
//读取该层的一维数组，将元素加入末尾
}else{
ArrayList<Integer> row = res.get(depth - 1);
row.add(root.val);
}
}
else
return;
//递归左右时深度记得加1
traverse(root.left, depth + 1);
traverse(root.right, depth + 1);
}
public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
if(root == null)
//如果是空，则直接返回
return res;
//递归层次遍历
traverse(root, 1);
return res;
}
}
广度优先遍历的变体-之字形输出
先从左到右，再从右到左输出。
还是使用队列，每一层从左往右遍历，再判断深度，根据深度信息来决定是否翻转某一行记录，翻转很容易，直接使用Collections.reverse(list)就可以。
只要是按照层输出的，随便它变，都在这里了。
import java.util.*;
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
ArrayList<ArrayList<Integer> > res = new ArrayList<ArrayList<Integer> >();
if (pRoot == null) return res;
queue.add(pRoot);
int depth = 1;
while(!queue.isEmpty()) {
ArrayList<Integer> list = new ArrayList<Integer>();
int size = queue.size();
for(int i = 0;i<size;i++) {
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
// 偶数行翻转
if(depth %2 == 0) Collections.reverse(list);
res.add(list);
depth++;
}
return res;
}
}
二叉树的深度
使用非递归方式
核心思想就是看看二叉树到底右多少层就行了。
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* }
*/
public class Solution {
/**
*
* @param root TreeNode类
* @return int整型
*/
public int maxDepth (TreeNode root) {
// write code here
Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
if(root == null) return 0;
queue.add(root);
int depth = 0;
while(!queue.isEmpty()) {
depth++;
int size = queue.size();
for(int i = 0;i<size;i++) {
TreeNode node = queue.poll();
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
}
return depth;
}
}
递归方式
从叶子节点回溯
左子树的和右子树中较大者+1；
public int maxDepth (TreeNode root) {
//递归方式
if(root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
二叉树到叶子节点路径上是否存在 和为某一个值的路径
我们只要能够遍历到叶子节点，并把路径上的和加上，然后判断就行。
可以递归，也可以使用非递归，借助队列和栈来实现 广度优先遍历和深度优先遍历。
递归实现
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* }
*/
public class Solution {
/**
*
* @param root TreeNode类
* @param sum int整型
* @return bool布尔型
*/
public boolean hasPathSum (TreeNode root, int sum) {
// write code here
if (root == null) return false;
if (root.left == null && root.right == null && sum - root.val == 0)
return true;
return hasPathSum(root.left, sum - root.val) ||
hasPathSum(root.right, sum - root.val);
}
}
非递归实现
- 通过广度优先遍历
参考广度优先遍历，我们能够直到每个节点的情况，如果我们再使用另一个队列来记录
public boolean hasPathSum (TreeNode root, int sum) {
// write code here
if (root == null) return false;
Queue<TreeNode> q1 = new ArrayDeque<TreeNode>();
Queue<Integer> q2 = new ArrayDeque<Integer>();
q1.add(root);
q2.add(root.val);
while (!q1.isEmpty()) {
int size = q1.size();
for (int i = 0; i < size; i++) {
TreeNode node = q1.poll();
int curSum = q2.poll();
// 叶子节点
if (node.left == null && node.right == null && sum == curSum) return true;
if(node.left != null) {
q1.add(node.left);
q2.add(node.left.val + curSum);
}
if(node.right != null) {
q1.add(node.right);
q2.add(node.right.val + curSum);
}
}
}
return false;
}
- 通过深度优先遍历
由于栈的特征是先进后出，那么可以实现深度遍历
public boolean hasPathSum (TreeNode root, int sum) {
// write code here
if (root == null) return false;
Stack<TreeNode> s1 = new Stack<TreeNode>();
Stack<Integer> s2 = new Stack<Integer>();
s1.push(root);
s2.push(root.val);
while (!s1.isEmpty()) {
TreeNode node = s1.pop();
int curSum = s2.pop();
//叶子节点
if(node.left == null && node.right == null && curSum == sum) return true;
// right先入栈，那么会先遍历左子树
if(node.right != null) {
s1.push(node.right);
s2.push(node.right.val + curSum);
}
if(node.left != null) {
s1.push(node.left);
s2.push(node.left.val + curSum);
}
}
return false;
}
二叉树和双向链表
这里明显就是中序遍历，我们使用栈来实现中序遍历，并将节点保持下来。
然后再处理节点之间的连接关系就可以了。
import java.util.*;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public TreeNode Convert(TreeNode pRootOfTree) {
// 其实题目就是典型的中序遍历
if(pRootOfTree == null) return null;
List<TreeNode> list = new ArrayList<TreeNode>();
Stack<TreeNode> s = new Stack<TreeNode>();
TreeNode root = pRootOfTree;
while(root != null || !s.isEmpty()) {
while(root != null) {
s.push(root);
root = root.left;
}
TreeNode node = s.pop();
list.add(node);
root = node.right;
}
// 将遍历结果链接成双向链表
TreeNode head = list.get(0);
head.left = null;
for(int i = 1;i<list.size();i++) {
list.get(i-1).right = list.get(i);
list.get(i).left = list.get(i-1);
}
list.get(list.size() -1).right = null;
return head;
}
}
合并二叉树
- 题目描述
已知两颗二叉树，将它们合并成一颗二叉树。合并规则是：都存在的结点，就将结点值加起来，否则空的位置就由另一个树的结点来代替。例如：
两颗二叉树是:
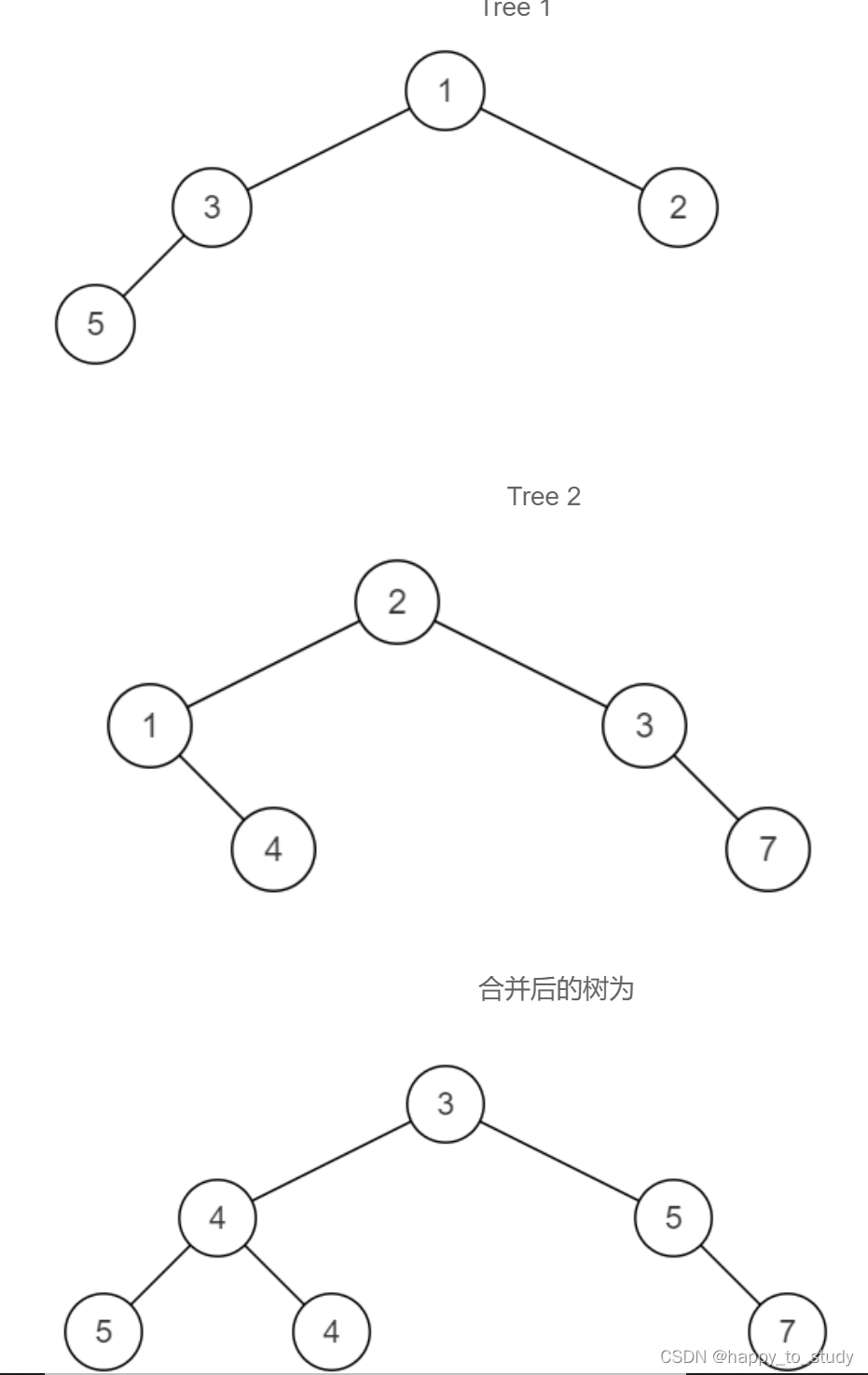
- 递归实现
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
// write code here
if(t1 == null) return t2;
if(t2 == null) return t1;
TreeNode newHead = new TreeNode(t1.val + t2.val);
newHead.left = mergeTrees(t1.left, t2.left);
newHead.right = mergeTrees(t1.right, t2.right);
return newHead;
}
- 非递归实现
这个是典型的层序遍历，所以使用队列来实现。
使用3个队列来存储遍历过程中的节点，一个用来放最终的结果；一个用于存放t1 ，一个用于存放t2.
遍历过程中检查，如果左右节点都不为空，则相加，且相应左右节点入队列；有一方为空，则直接用某一方的节点，且不必再入队遍历了；
public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
// write code here
if (t1 == null) return t2;
if (t2 == null) return t1;
TreeNode head = new TreeNode(t1.val + t2.val);
Queue<TreeNode> q = new LinkedList<>();
Queue<TreeNode> q1 = new LinkedList<>();
Queue<TreeNode> q2 = new LinkedList<>();
q.offer(head);
q1.offer(t1);
q2.offer(t2);
while (!q1.isEmpty() && !q2.isEmpty()) {
TreeNode node = q.poll();
TreeNode node1 = q1.poll();
TreeNode node2 = q2.poll();
if (node1.left != null || node2.left != null) {
if (node1.left != null && node2.left != null) {
TreeNode left = new TreeNode(node1.left.val + node2.left.val);
node.left = left;
q.offer(left);
q1.offer(node1.left);
q2.offer(node2.left);
} else if (node1.left != null)
node.left = node1.left;
else
node.left = node2.left;
}
if (node1.right != null || node2.right != null) {
if (node1.right != null && node2.right != null) {
TreeNode right = new TreeNode(node1.right.val + node2.right.val);
node.right = right;
q.offer(right);
q1.offer(node1.right);
q2.offer(node2.right);
} else if (node1.right != null)
node.right = node1.right;
else
node.right = node2.right;
}
}
return head;
}
二叉树镜像
- 递归方案
public TreeNode Mirror (TreeNode pRoot) {
// write code here
doMirror(pRoot);
return pRoot;
}
private void doMirror(TreeNode pRoot) {
if (pRoot == null) return;
TreeNode left = pRoot.left;
TreeNode right = pRoot.right;
pRoot.left = right;
pRoot.right = left;
doMirror(left);
doMirror(right);
}
- 非递归方案
public TreeNode Mirror (TreeNode pRoot) {
// write code here
if(pRoot == null) return null;
Stack<TreeNode> s = new Stack<>();
s.push(pRoot);
while(!s.isEmpty()) {
TreeNode node = s.pop();
if(node.left != null) s.push(node.left);
if(node.right != null) s.push(node.right);
TreeNode t = node.left;
node.left = node.right;
node.right = t;
}
return pRoot;
}
判断一棵树是否是二叉搜索树
二叉搜索树满足： 左节点的值都小于根，右节点的值都大于根节点。
进一步，其中序遍历是严格递增的。
所以我们只要拿到中序遍历序列，再判断是否递增就行了。
public boolean isValidBST (TreeNode root) {
if (root == null) return true;
Stack<TreeNode> s = new Stack<>();
ArrayList<Integer> sort = new ArrayList<>(); // 存放中序遍历结果
TreeNode node = root;
while (node != null || !s.isEmpty()) {
while (node != null) {
s.push(node);
node = node.left;
}
node = s.pop();
sort.add(node.val);
node = node.right;
}
//
for (int i = 1; i < sort.size(); i++) {
if (sort.get(i) < sort.get(i - 1)) {
return false;
}
}
return true;
}
判断是否是完全二叉树
完全二叉树的定义：若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树。（第 h 层可能包含 [1~2h] 个节点）
public boolean isCompleteTree (TreeNode root) {
// write code here
if (root == null) return true;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
boolean visitNull = false;
while (!q.isEmpty()) {
TreeNode node = q.poll();
// 已经到叶子节点了，后续不能再有非空的元素的
if(node == null) {
visitNull = true;
continue;
}
if(visitNull) return false;
q.offer(node.left);
q.offer(node.right);
}
return true;
}
判断是否是平衡二叉树
输入一棵节点数为 n 二叉树，判断该二叉树是否是平衡二叉树。
在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树
平衡二叉树（Balanced Binary Tree），具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
- 递归方式
计算左子树的深度和右子树的深度差是否不大于1， 然后再递归判断左右子树是否也满足。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if(root == null) return true;
int left = depth(root.left);
int right = depth(root.right);
if(Math.abs(right-left) > 1) return false;
return IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
private int depth(TreeNode root) {
if(root == null) return 0;
return Math.max(depth(root.left), depth(root.right)) + 1;
}
}
重建二叉树
根据前序和中序序列，构建二叉树
- 递归方式
import java.util.*;
public class Solution {
//前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
public TreeNode reConstructBinaryTree(int [] pre, int [] vin) {
int n = pre.length;
int m = vin.length;
if(n == 0 || m == 0) return null;
TreeNode root = new TreeNode(pre[0]);
for(int i=0;i<vin.length;i++) {
// 找到根节点 在中序中的位置
if(pre[0] == vin[i]) {
root.left = reConstructBinaryTree(
Arrays.copyOfRange(pre, 1, i+1),
Arrays.copyOfRange(vin, 0, i)
);
root.right = reConstructBinaryTree(
Arrays.copyOfRange(pre, i+1, n),
Arrays.copyOfRange(vin, i+1, m)
);
}
}
return root;
}
}
- 非递归实现
public TreeNode reConstructBinaryTree(int [] pre, int [] vin) {
int n = pre.length;
int m = vin.length;
//每个遍历都不能为0
if (n == 0 || m == 0)
return null;
Stack<TreeNode> s = new Stack<TreeNode>();
//首先建立前序第一个即根节点
TreeNode root = new TreeNode(pre[0]);
TreeNode cur = root;
for (int i = 1, j = 0; i < n; i++) {
//要么旁边这个是它的左节点
if (cur.val != vin[j]) {
cur.left = new TreeNode(pre[i]);
s.push(cur);
//要么旁边这个是它的右节点，或者祖先的右节点
cur = cur.left;
} else {
j++;
//弹出到符合的祖先
while (!s.isEmpty() && s.peek().val == vin[j]) {
cur = s.pop();
j++;
}
//添加右节点
cur.right = new TreeNode(pre[i]);
cur = cur.right;
}
}
return root;
}
扫一扫
752
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
