Java 遍历二叉树

LL_break

已于 2025-05-12 14:13:22 修改

阅读量830

点赞数 16

CC 4.0 BY-SA版权

文章标签：算法 java 数据结构二叉树

于 2025-05-11 23:54:51 首次发布

本文链接：https://blog.youkuaiyun.com/LL_break/article/details/147878514

回顾

二叉树
任意节点的度，不能超过2的树

存储二叉树

孩子表示法
class Node { // 某个节点只有左子树，没有右子树

String val; right == null;

Node left; // 右子树

Node right; // 左子树

}

遍历二叉树

二叉树的核心操作
把所有的节点，按一定的次序，全部访问（针对这个数据，进行各种操作如：打印，修改，判定，计算......）一遍，访问过程中“不重不漏”。

4种遍历方法
关键是约定好非线性结果的遍历顺序
分为：先序遍历、中序遍历、后序遍历、层序遍历

1.先序遍历

基于递归

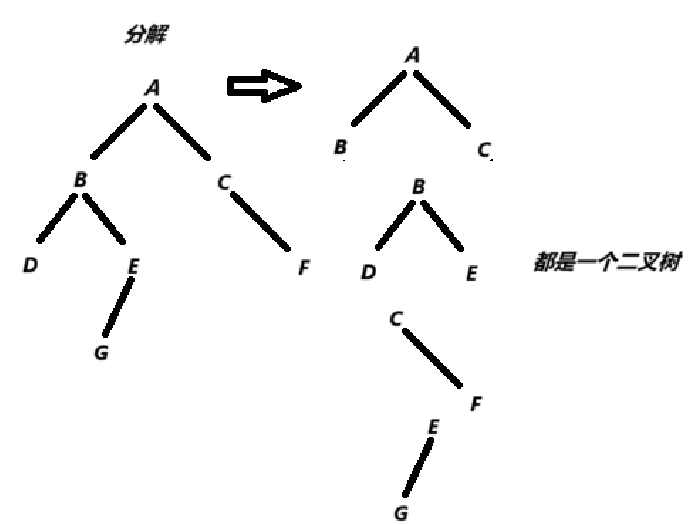
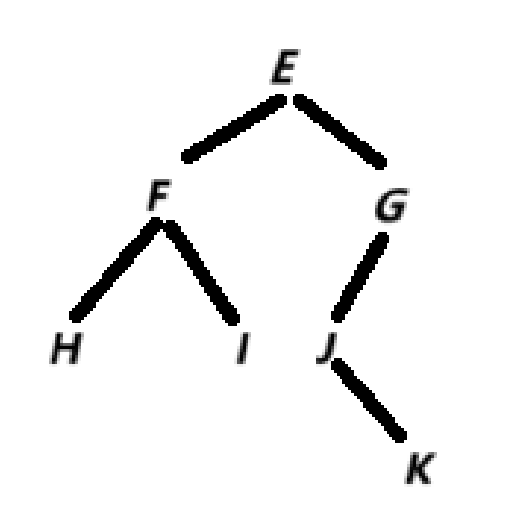
以下递归展开都以此图为例

过程

从根节点出发
1.先访问当前节点的值
2.递归的针对左子树进行先序遍历
3.递归的针对右子树进行先序遍历

递归展开

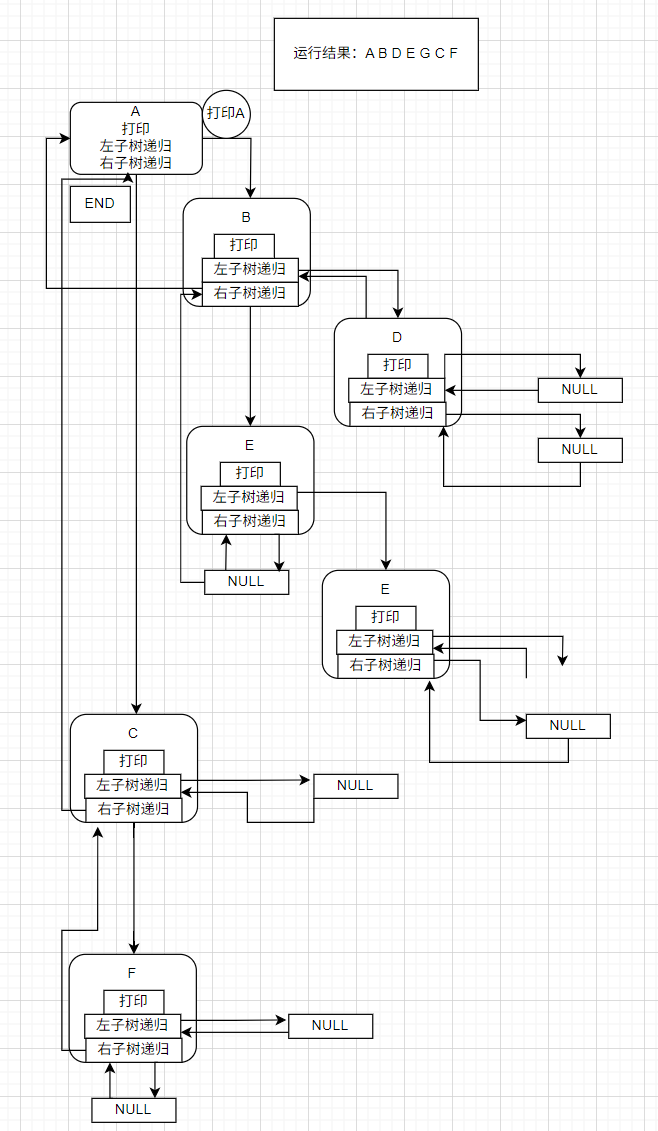
代码

// 先序遍历
public static void preOrder(Node root){
        if(root == null){
            return;
        }
        System.out.print(root.val + " ");  // 访问根节点（以下都以打印为例）
        preOrder(root.left);               // 递归左子树
        preOrder(root.right);              // 递归右子树

    }

2.中序遍历

基于递归

过程

1.先递归左子树
2.访问根节点
3.递归右子树

递归展开

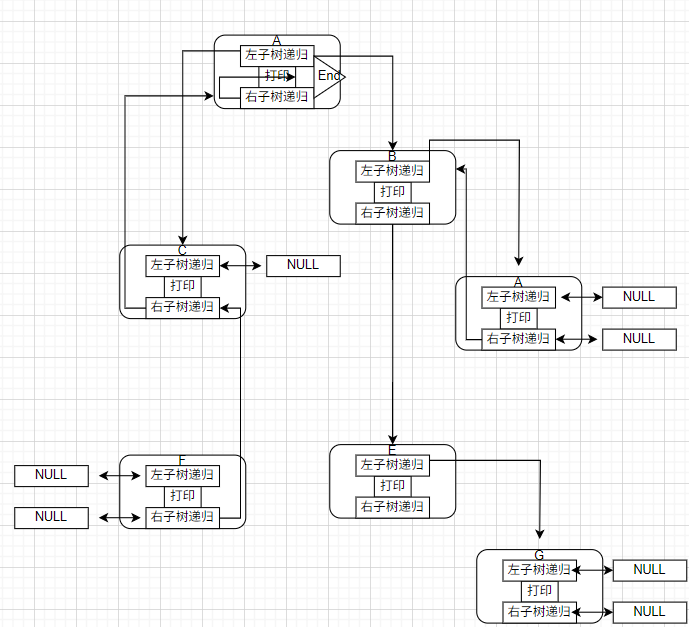
代码

// 中序遍历
    public static void inOrder(Node root){
        if(root == null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

3.后序遍历

同样基于递归

过程

1.先递归左子树
2.递归右子树
3.访问根节点

递归展开

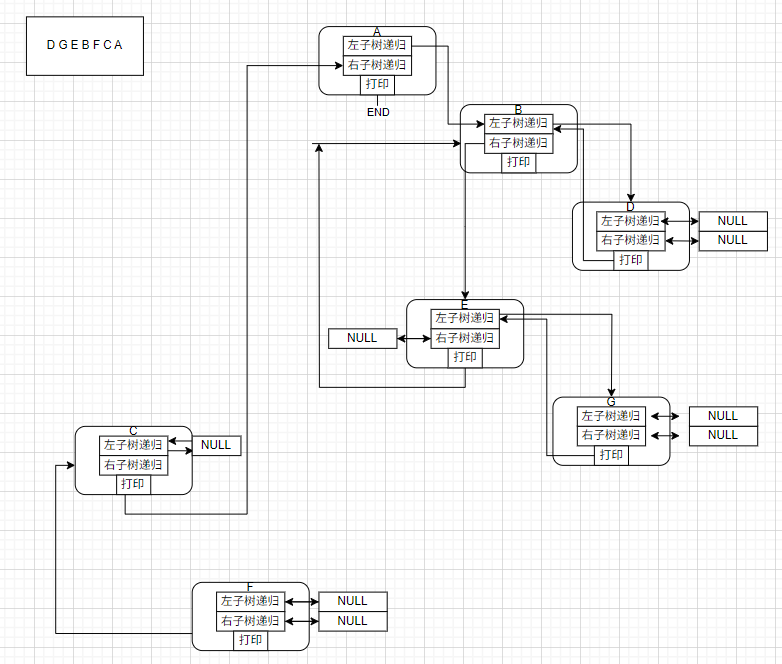
代码

// 后序遍历
    public static void postOrder(Node root){
        if(root == null){
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val + " ");
    }

4.层序遍历

按照层为维度，把每一层的元素从左到右的访问一遍

过程

1.先递归左子树
2.递归右子树
3.访问根节点

实现需要搭配一个队列：
1、创建队列，队列元素就是 Node ，先把根节点入队列
2、循环的取出对首元素访问元素值
3、把这个元素的左子数和右子树都分别入队列，前提是非空
4、回到第二步进行循环
5、队列为空遍历即结束

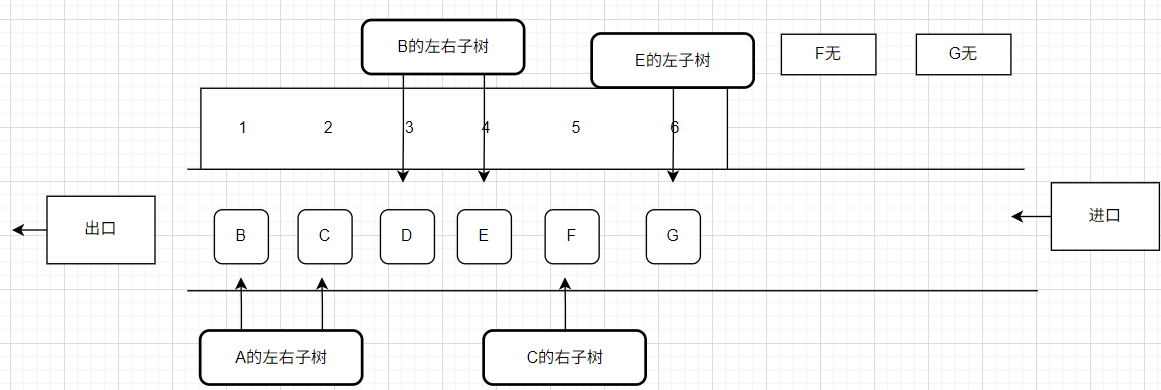
结果 A B C D E F G

代码

// 层序遍历
    public static void levelOrder(Node root){
        if(root == null){
            return;
        }
        // 创建一个队列，辅助层序遍历
        Queue<Node> queue = new LinkedList<>();
        // 根节点入队列
        queue.offer(root);

        while(!queue.isEmpty()){
            // 取出队首元素
            Node cur = queue.poll();
            // 访问元素
            System.out.print(cur.val + "");
            // 把左右子树连续入队列
            if(cur.left != null){
                queue.offer(cur.left);
            }
            if(cur.right != null){
                queue.offer(cur.right);
            }
        }
    }

还原🌳

已知：先/后序 + 中序结果
例子：

先序： E F H I G J K
中序： H F I E J K G

1 先序第一个元素为根节点

2.在中序中左子树在根节点左侧

  拿着根节点E在中序中找
3.对照着先序
  FHI为左子树的先序
  GJK为右子树的先序
4.针对左子数进行还原

先序 FHI   确定F为左子树的根节点，

拿着F去中序中找，

H是F的左子树，I为F的右子树

中序 HFI

5.针对右子树进行还原

先序 GJK G为右子树的根
中序 JKG G的左子树是JK 右子树为空
6.针对G的左子树还原
先序 JK J为G的左子树的根
中序 JK J为G的左子树的右子树

还原结果：