【算法竞赛】二分+单调队列经典应用（附详细思路和图解）

本文将从预备知识到解题思路再到代码详细介绍一道洛谷上经典的二分+单调队列的融合知识点题目，同时还涉及到前缀和等算法竞赛思想和技巧，是一道难度较高，但知识点覆盖较多的题目，作为竞赛练习非常有帮助

目录

预备知识1——二分法

预备知识2——单调队列

题目 

思路详解（从0开始）

代码

预备知识1——二分法

        二分法在之前的博客（数据结构与算法——二分查找_二分查找 开闭区间-优快云博客）中做过详细介绍，包括查找确切值、最大值最小化、最小值最大化等等，之前介绍的都是整数二分，本题用到的是实数二分，二者的区别并不大，思想都是一样的，只是实数二分少了向上取整这个环节，所以在mid和left、right的处理上有些不同。

预备知识2——单调队列

       单调队列在之前的博客（【洛谷】P1886 滑动窗口 /【模板】单调队列，经典！-优快云博客）中也作过详细介绍。

       单调队列既可以针对定长区间，也可以针对不定长区间，之前介绍的是属于定长区间，而针对不定长区间也没有什么区别，都是：

• 确定锚点
• 比较队尾和距离当前锚点i最近的点，看是否满足单调性，不满足单调性的从队尾出队
• 距离当前锚点i最近的点入队
• 比较队头，是否位于距离锚点i最远的点的范围内，不满足从队头出

单调队列做多了会发现它的核心就是：确定锚点+与锚点相关的一段区间，求区间内的特定值（通常是min或max），如果是min就维护一个单调递增的队列，如果是max就维护一个单调递减序列，至于代码模板就是上面写的四步曲

题目 

P1419 寻找段落 - 洛谷【普及+/提高】

思路详解（从0开始）

• 拿到题目，审题，容易判断答案具有单调性 ——>想到二分
• 输出为double类型——>实数二分
• 二分常常搭配——>check，作为判定条件
• 本题的check——>是否存在一个段落满足正在尝试的平均长度
• 既然是和平均长度作比较——>每一个段的长度可以先做一个预处理，减去平均长度，可以得到其和平均长度的差值，这样后面比较起来就非常方便
• 段落长度如何计算——>段落连续——>前缀和sum
• 计算完段落长度以后如何比较——>段落长度越大越好，越大越可能满足正在尝试的平均长度——>段落不定长——>用单调队列维护

以上就是从题目本身开始思考，一步步延申出的思维过程，有了上面的思路，其实就是代码细节处理和实现的问题了，下面将介绍几个比较容易出错和核心的点

假设我们的段落排列如下：

首先如何满足长度条件？

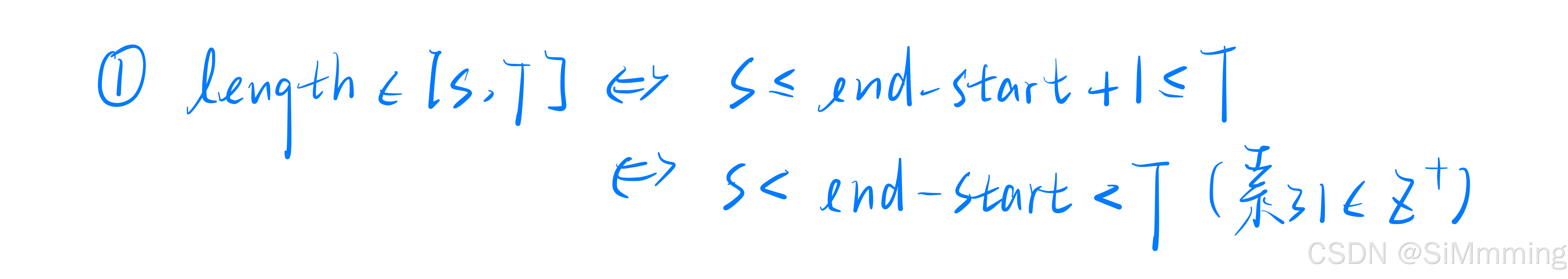
其次我们要求的是什么？

解决了上面几个问题以后，代码的边界条件便可以基本确定下来了，这几张图非常关键，有助于帮大家理解check中的边界设置问题，也是本题中最容易WA的地方。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, s, t;
double val[N];//元素原始价值
double nval[N];//元素原始价值-平均价值
double sum[N];//前缀和
deque<int> q;//单调队列，存放索引
//是否存在段落平均值满足条件
bool check(double x)
{
	for (int i = 1; i <= n; i++) nval[i] = val[i] - x;
	//前缀和
	sum[0] = 0;
	for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + nval[i];
	//段落和
	//确定终点找起点
	//终点-起点区间：1、长度[s,t]，2、起点前缀和min
	//转换为：维护队头min的单调队列
	q.clear();
	for (int i = 1; i <= n; i++)
	{
		//区间开始移动
		if (i >= s)
		{
			//最近起始点
			while (!q.empty() && sum[i - s] <= sum[q.back()]) q.pop_back();
			q.push_back(i - s);
		}
		//q.push_back(i - s + 1);
		//最远起始点
		while (!q.empty() && i - q.front()> t) q.pop_front();
		//段落长度符合条件+大于等于平均值，存在
		if (!q.empty() && i - q.front() >= s && sum[i] - sum[q.front()] >= 0)return true;
	}
	return false;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> s >> t;
	for (int i = 1; i <= n; i++) cin >> val[i];
	double l = -10000, r = 10000;//题给条件
	//左闭右开区间
	while (r - l>1e-5)
	{
		double mid = (l + r) / 2;
		//当前平均值存在，还可以更大
		if (check(mid))l = mid;
		else r = mid;
	}
	printf("%.3f", l);
}