代码随想录Day1：数组（二分、移除、有序数组的平方）

一、理论

• 数组存放空间连续、类型相同的数据集合，下标从0开始
• 地址连续->增删会带起一连串的移动->增删元素困难
• 数组和链表不同，元素只能覆盖，并没有实际意义上的删除

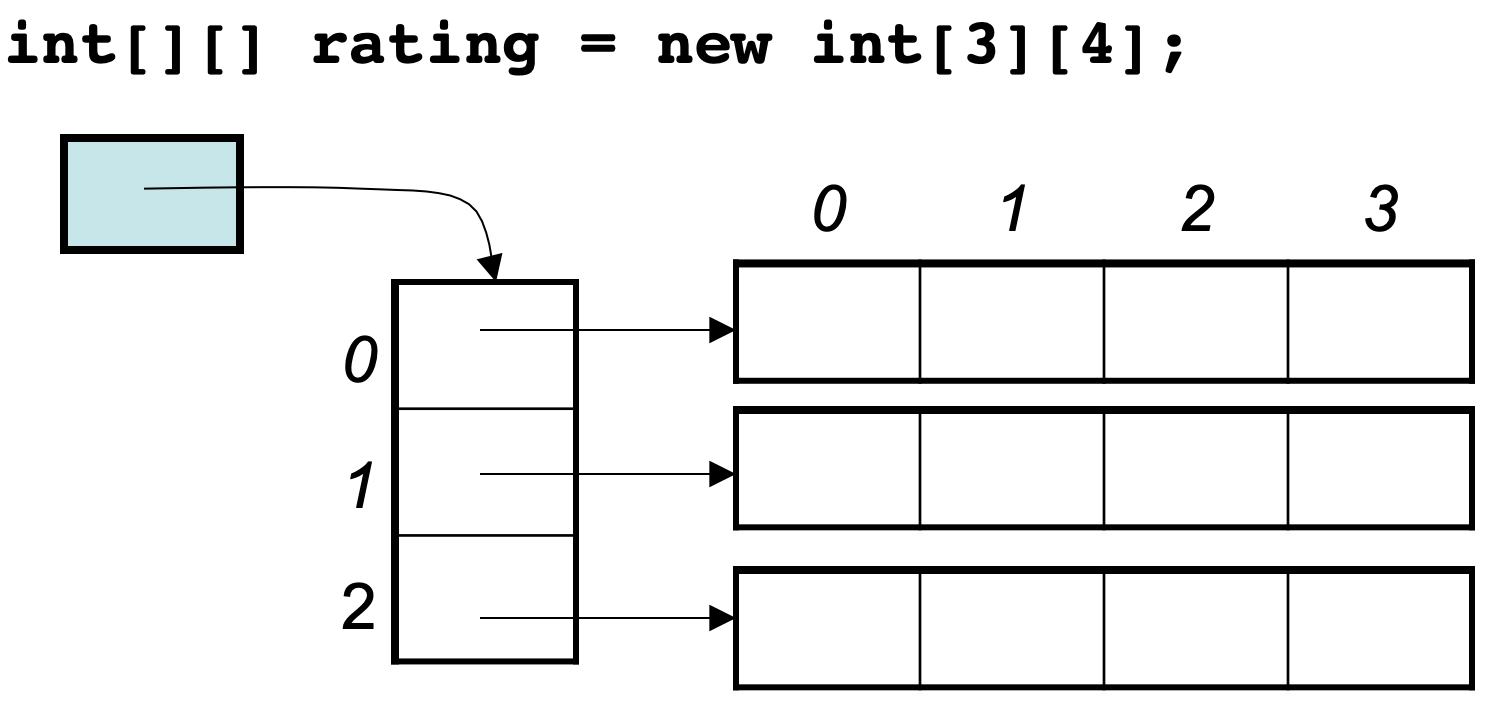
拓展：二维数组在内存中的存放是否连续？

• C++是连续分布的

void test_arr() {
    int array[2][3] = {
		{0, 1, 2},
		{3, 4, 5}
    };
    cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
    cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}

int main() {
    test_arr();
}

0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834

• Java中没有指针，寻址操作完全交给虚拟机

public static void test_arr() {
    int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
    System.out.println(arr[0]);
    System.out.println(arr[1]);
    System.out.println(arr[2]);
    System.out.println(arr[3]);
}

所得到的每行头结点地址没有规则，排列方式可能如下

二、实战

704二分查找

704. 二分查找 - 力扣（LeetCode）704. 二分查找 - 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。你必须编写一个具有 O(log n) 时间复杂度的算法。示例 1:输入: nums = [-1,0,3,5,9,12], target = 9输出: 4解释: 9 出现在 nums 中并且下标为 4示例 2:输入: nums = [-1,0,3,5,9,12], target = 2输出: -1解释: 2 不存在 nums 中因此返回 -1 提示： 1. 你可以假设 nums 中的所有元素是不重复的。 2. n 将在 [1, 10000]之间。 3. nums 的每个元素都将在 [-9999, 9999]之间。https://leetcode.cn/problems/binary-search/

二分查找前提：数组有序

边界处理原则：左闭右闭

package org.example;

public class BinarySearch704 {
    public int search(int[] nums, int target) {
        //区间处理原则：左闭右闭
        int i=0;
        int j=nums.length-1;
        int m;
        while(i<=j)
        //取等：[1,1]也是有效的，所以可取等
        {
            m=(i+j)/2;
            if(nums[m]==target)
                return m;
            else if(nums[m]>target)
            {
                //区间处理原则：左闭右闭
                //因此不能把这部分处理过的边界再算进来
                j=m-1;
            }
            else{
                i=m+1;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        BinarySearch704 b=new BinarySearch704();
        int[] nums={-1,0,3,5,9,12};
        int target=9;
        System.out.println(b.search(nums,target));
        //返回4，正确
    }
}

边界处理原则：左闭右开

  public int search(int[] nums, int target) {
        //区间处理原则：左闭右开
        int i=0;
        int j=nums.length;
        int m;
        while(i<j)
        //取等：[1,1）无效，所以不可取等
        {
            m=(i+j)/2;
            if(nums[m]==target)
                return m;
            else if(nums[m]>target)
            {
                //区间处理原则：左闭右开
                //因此能把这部分处理过的边界再算进来
                j=m;
            }
            else{
                i=m+1;
            }
        }
        return -1;
    }

27移除元素

 暴力破解法——抓住有效位数的变化

package org.example;

public class removeElement27 {

    public int removeElement(int[] nums, int val) {
        int temp=nums.length;//有效位数
        for(int i=0;i<temp;i++)
        {
            if(nums[i]==val)
            {
                for(int j=i+1;j<nums.length;j++)
                {
                    nums[j-1]=nums[j];
                }
                i--;//往前移动之后，i还是测试之前的位置
                temp--;//查出一个val目标值，有效位数-1
            }
        }
        System.out.print(temp+", nums = [");
        for(int i=0;i<nums.length-1;i++)
        {
            System.out.print(nums[i]+",");
        }
        //边界值，当nums中有效位数为0时特殊处理
        if(temp!=0) System.out.println(nums[nums.length-1]+"]");
        return temp;
    }

    public static void main(String[] args) {
        removeElement27 b=new removeElement27();
        int[] nums={0,1,2,2,3,0,4,2};
        int target=2;
        b.removeElement(nums,target);
    }
}

快慢指针法——fast用于遍历所有，slow用于指示有效的数组

 public int removeElement(int[] nums, int val) {
        // 快慢指针
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
            }
        }
        System.out.print(slowIndex+", nums = [");
        for(int i=0;i<nums.length-1;i++)
        {
            System.out.print(nums[i]+",");
        }
        //边界值，当nums中有效位数为0时特殊处理
        if(slowIndex!=0) System.out.println(nums[nums.length-1]+"]");
        return slowIndex;
    }

977有序数组的平方

前提：开始数组是非递减

直观——暴力破解

1.平方 2.排序 3.输出

其中排序如果使用相对复杂度低的排序，则时间复杂度是 O(n + nlogn)，此处 O(n*n)

package org.example;
public class sortedSquares977 {
    public int[] sortedSquares(int[] nums) {
        //1.平方
        for(int i=0;i<nums.length;i++)
        {
            nums[i]=nums[i]*nums[i];
        }
        //2.排序（可以配合库函数使用Array.sort)
        for(int i=0;i<nums.length;i++)
        {
            for(int j=i+1;j<nums.length;j++)
            {
                if(nums[j]<nums[i])
                {
                    int temp=nums[i];
                    nums[i]=nums[j];
                    nums[j]=temp;
                }
            }
        }

        //输出
        System.out.println("[");
        for(int i=0;i<nums.length-1;i++)
        {
            System.out.print(nums[i]+",");
        }
        System.out.println(nums[nums.length-1]+"]");


        return nums;
    }
    
    public static void main(String[] args) {
        sortedSquares977 b=new sortedSquares977();
        int[] nums={-4,-1,0,3,10};
        int[] nums2=b.sortedSquares(nums);
        for(int i=0;i<nums.length-1;i++)
        {
            System.out.print(nums2[i]+",");
        }
        System.out.println(nums2[nums2.length-1]+"]");
    }
}

双指针法——因为一开始数组非递减，则平方之后左右两头大中间小

class Solution {
    public int[] sortedSquares(int[] nums) {
        int l = 0;
        int r = nums.length - 1;
        int[] res = new int[nums.length];
        int j = nums.length - 1;
        while(l <= r){
            if(nums[l] * nums[l] > nums[r] * nums[r]){
                res[j--] = nums[l] * nums[l++];
            }else{
                res[j--] = nums[r] * nums[r--];
            }
        }
        return res;
    }
}