OpenCV ---图像预处理（一）

OpenCV —图像预处理（一）

---

---

一、图像翻转

在OpenCV中，图片的镜像旋转是以图像的中心为原点进行镜像翻转的。

• cv2.flip(img,flipcode)

• 参数

  • img: 要翻转的图像
  • flipcode: 指定翻转类型的标志
    • flipcode=0: 垂直翻转，图片像素点沿x轴翻转
    • flipcode>0: 水平翻转，图片像素点沿y轴翻转
    • flipcode<0: 水平垂直翻转,水平翻转和垂直翻转的结合

#图像翻转,cv.flip(img, 翻转类型标志)
cat = cv.imread('txycl/images/cat1.png')
cat = cv.resize(cat, (500, 500))
#垂直翻转
cat1=cv.flip(cat, 0)
#水平翻转
cat2=cv.flip(cat, 1)
#垂直水平翻转
cat3=cv.flip(cat, -1)
cv.imshow('cat', cat)
cv.imshow('cat1', cat1)
cv.imshow('cat2', cat2)
cv.imshow('cat3', cat3)
cv.waitKey(0)
cv.destroyAllWindows()

二、图像仿射变换

​ 仿射变换（Affine Transformation）是一种线性变换,保持了点之间的相对距离不变。

• 仿射变换的基本性质

  • 保持直线
  • 保持平行
  • 比例不变性
  • 不保持角度和长度

• 常见的仿射变换类型

  • 旋转：绕着某个点或轴旋转一定角度。
  • 平移：仅改变物体的位置，不改变其形状和大小。
  • 缩放：改变物体的大小。
  • 剪切：使物体发生倾斜变形。
    仿射变换的基本原理

• 线性变换

• 二维空间中，图像点坐标为$(x,y)$，仿射变换的目标是将这些点映射到新的位置 $(x^{\prime },y^{\prime })$。

• 为了实现这种映射，通常会使用一个矩阵乘法的形式：

  （类似于y=kx+b）
  

• $a$，$b$，$c$，$d$是线性变换部分的系数，控制旋转、缩放和剪切。

• $t_x$，$t_y$ 是平移部分的系数，控制图像在平面上的移动。

• 输入点的坐标被扩展为齐次坐标形式$[x,y,1]$，以便能够同时处理线性变换和平移
  

cv2.warpAffine(img,M,dsize)

• img：输入图像。

• M：2x3的变换矩阵，类型为np.float32。

• dsize：输出图像的尺寸，形式为(width,height)。

2.1 图像旋转

旋转图像可以将图像绕着某个点旋转一定的角度。

cv2.getRotationMatrix2D()函数

• 获取旋转矩阵

  cv2.getRotationMatrix2D(center,angle,scale)
  

  • center：旋转中心点的坐标，格式为(x,y)。
  • angle：旋转角度，单位为度，正值表示逆时针旋转负值表示顺时针旋转。
  • scale：缩放比例，若设为1，则不缩放。
  • 返回值：M，2x3的旋转矩阵。

#图像仿射变换
#图像旋转
img = cv.imread('txycl/images/cat1.png')
h,w,_ = img.shape
#设置旋转中心点
center = (w//2, h//2)
#设置旋转角度
angle = 45
#设置缩放系数
scale = 0.5
#获取旋转矩阵
M = cv.getRotationMatrix2D(center, angle, scale)
cat1 = cv.warpAffine(img, M, (w, h))
cv.imshow('cat', img)
cv.imshow('new_cat', cat1)
cv.waitKey(0)
cv.destroyAllWindows()

2.2 图像平移

移操作可以将图像中的每个点沿着某个方向移动一定的距离。

• 假设我们有一个点 $P(x,y)$，希望将其沿x轴方向平移$t_x$*个单位，沿y轴方向平移$t_y$个单位到新的位置$P\prime (x\prime ,y\prime )$，那么平移公式如下：

  ​ $x\prime =x+tx$

  ​ $y\prime =y+ty$

  在矩阵形式下，该变换可以表示为：
  这里的$t_x$和$t_y$分别代表在x轴和y轴上的平移量。
  

#图像平移
img = cv.imread('txycl/images/cat1.png')
h,w,_ = img.shape
#平移距离
tx,ty = 100,100
#平移矩阵
M = np.float32([[1,0,tx],[0,1,ty]])
#平移变换
cat1 = cv.warpAffine(img, M, (w, h))
cv.imshow('cat', img)
cv.imshow('new_cat', cat1)
cv.waitKey(0)
cv.destroyAllWindows()

2.3 图像缩放

缩放操作可以改变图片的大小。

• 假设要把图像的宽高分别缩放为0.5和0.8，那么对应的缩放因子sx=0.5，sy=0.8。

• 点$P(x,y)$对应到新的位置$P^{\prime }(x^{\prime },y^{\prime })$，缩放公式为：

  $x\prime =s_x\ast x$

  ​ $y\prime =s_y\ast y$

  在矩阵形式下，该变换可以表示为：
  

#图像缩放
img = cv.imread('txycl/images/cat1.png')
#缩放系数
sx =0.5
sy =0.8
#缩放矩阵
M =np.float32([[sx,0,0],[0,sy,0]])
#缩放变换
cat1 = cv.warpAffine(img, M, (img.shape[1], img.shape[0]))
cv.imshow('cat', img)
cv.imshow('new_cat', cat1)
cv.waitKey(0)
cv.destroyAllWindows()

2.4 图像剪切

剪切操作可以改变图形的形状，以便其在某个方向上倾斜，它将对象的形状改变为斜边平行四边形，而不改变其面积。

• 想象我们手上有一张矩形纸片，如果你固定纸片的一边，并沿着另一边施加一个平行于该边的力，这张纸片就会变形为一个平行四边形。这就是剪切变换的一个直观解释。

• 对于二维空间中的点$P(x,y)$，对他进行剪切变换：

  沿x轴剪切：$x^{\prime }=x+s{h}_y\ast y$ $y^{\prime }=y$

  沿y轴剪切：$x^{\prime }=x$ $y^{\prime }=s{h}_x\ast x+y$

• 当需要同时沿两个方向进行剪切时，$x^{\prime }=x+s{h}_y\ast y$ ， $y^{\prime }=s{h}_x\ast x+y$
  
  
  

三，插值方法

在图像处理和计算机图形学中，插值（Interpolation）是一种通过已知数据点之间的推断或估计来获取新数据点的方法。它在图像处理中常用于处理图像的放大、缩小、旋转、变形等操作，以及处理图像中的像素值。

图像插值算法是为了解决图像缩放或者旋转等操作时，由于像素之间的间隔不一致而导致的信息丢失和图像质量下降的问题。当我们对图像进行缩放或旋转等操作时，需要在新的像素位置上计算出对应的像素值，而插值算法的作用就是根据已知的像素值来推测未知位置的像素值。

3.1 最近领插值

CV2.INTER_NEAREST

new_img1=cv.warpAffine(img,M,(w,h),flags=cv.INTER_NEAREST)

首先给出目标点与原图像点之间坐标的计算公式：

​ $$srcX=dstX\ast \frac{srcWidth}{dstWidth}$$

​ $$srcY=dstY\ast \frac{srcHeight}{dstHeight}$$

• $dstX$：目标图像中某点的x坐标，
• $dstY$：目标图像中某点的$y$坐标，
• $srcWidth$：原图的宽度，
• $dstWidth$：目标图像的宽度；
• $srcHeight$：原图的高度，
• $dstHeight$：目标图像的高度。
• 而$srcX$和$srcY$：目标图像中的某点对应的原图中的点的$x$$和$y$的坐标。
  -示例
  
  
  
  
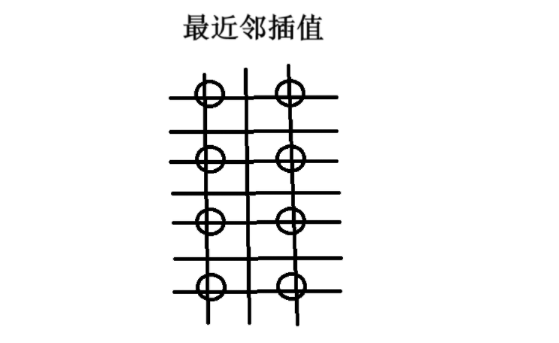
• 代码

#最近邻插值
pig = cv.imread('txycl/images/pig.png')
pig = cv.resize(pig, (750, 500))
h,w=pig.shape[:2]
center = (w//2, h//2)
#获取旋转矩阵
M = cv.getRotationMatrix2D(center,0,0.5)
img1 = cv.warpAffine(pig, M, (w, h), flags=cv.INTER_NEAREST)
cv.imshow('pig', pig)
cv.imshow('new_pig', img1)
cv.waitKey(0)
cv.destroyAllWindows()

3.2 双线性插值

双线性插值是一种图像缩放、旋转或平移时进行像素值估计的插值方法。当需要对图像进行变换时，特别是尺寸变化时，原始图像的某些像素坐标可能不再是新图像中的整数位置，这时就需要使用插值算法来确定这些非整数坐标的像素值。

双线性插值的工作原理是这样的：

1. 假设要查找目标图像上坐标为 (x', y') 的像素值，在原图像上对应的浮点坐标为 (x, y)。

2. 在原图像上找到四个最接近(x, y)的像素点，通常记作 P00(x0, y0), P01(x0, y1), P10(x1, y0), P11(x1, y1)，它们构成一个2x2的邻域矩阵。

3. 分别在水平方向和垂直方向上做线性插值：

• 水平方向：根据 x 与 x0 和 x1 的关系计算出 P00 和 P10 、 P01和 P11 之间的插值结果。

• 垂直方向：将第一步的结果与 y 与 y0 和 y1 的关系结合，再在垂直方向上做一次线性插值。

4. 综合上述两次线性插值的结果，得到最终位于 (x', y') 处的新像素的估计值。

#双线性插值
pig = cv.imread('txycl/images/pig.png')
pig = cv.resize(pig, (750, 500))
h,w=pig.shape[:2]
center = (w//2, h//2)
M = cv.getRotationMatrix2D(center,0,0.5)
img1 = cv.warpAffine(pig, M, (w, h), flags=cv.INTER_LINEAR)
cv.imshow('pig', pig)
cv.imshow('new_pig', img1)
cv.waitKey(0)
cv.destroyAllWindows()

3.3 像素区域差值

cv2.INTER_AREA

• 当使用像素区域插值方法进行放大图像时
  • 如果图像放大的比例是整数倍，那么其工作原理与最近邻插值类似；
  • 如果放大的比例不是整数倍，那么就会调用双线性插值进行放大。

其中目标像素点与原图像的像素点的对应公式如下所示：
$$srcX=dstX\ast \frac{srcWidth}{dstWidth}$$

$$srcY=dstY\ast \frac{srcHeight}{dstHeight}$$

#像素区域插值
pig = cv.imread('txycl/images/pig.png')
pig = cv.resize(pig, (750, 500))
h,w=pig.shape[:2]
center = (w//2, h//2)
M = cv.getRotationMatrix2D(center,0,0.5)
img1 = cv.warpAffine(pig, M, (w, h), flags=cv.INTER_LINEAR)
cv.imshow('pig', pig)
cv.imshow('new_pig', img1)
cv.waitKey(0)
cv.destroyAllWindows()

3.4 双三次插值

与双线性插值法相同，该方法也是通过映射，在映射点的邻域内通过加权来得到放大图像中的像素值。不同的是，双三次插值法需要原图像中近邻的16个点来加权,也就是4x4的网格。

目标像素点与原图像的像素点的对应公式如下所示：
$$srcX=dstX\ast \frac{srcWidth}{dstWidth}$$

$$srcY=dstY\ast \frac{srcHeight}{dstHeight}$$

下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的16个像素点作为计算目标图像B（X,Y）处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素（x,y）的值就等于16个像素点的加权叠加。
代码

#双三次插值
img1 = cv.warpAffine(pig, M, (w, h),flags=cv.INTER_CUBIC)

3.5 Lanczos插值

Lanczos插值方法与双三次插值的思想是一样的，不同的就是其需要的原图像周围的像素点的范围变成了8*8，并且不再使用BiCubic函数来计算权重，而是换了一个公式计算权重。

首先还是目标像素点与原图像的像素点的对应公式如下所示：
$$srcX=dstX\ast \frac{srcWidth}{dstWidth}$$

$$srcY=dstY\ast \frac{srcHeight}{dstHeight}$$

下面我们举例说明，假设原图像A大小为m*n，缩放后的目标图像B的大小为M*N。其中A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一个像素点（X,Y）的值，必须先找出像素（X,Y）在原图像A中对应的像素（x,y），再根据原图像A距离像素（x,y）最近的64个像素点作为计算目标图像B（X,Y）处像素值的参数，利用权重函数求出64个像素点的权重，图B像素（x,y）的值就等于64个像素点的加权叠加。

#Lanczos4插值
img1 = cv.warpAffine(pig, M, (w, h), flags=cv.INTER_LANCZOS4)