目录
3.返回: 最终的最大利润是不持有股票的最大利润(一定要卖光)
问题描述
为了奖励你在上个季度的优秀表现,公司决定发给你一部分股票,你可以在市场上自由交易。
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格。
设计一个算法计算出最大利润。
在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
- 卖出股票后,你无法在第二天买入股票(即冷冻期为 1 天)
输入格式
一个数组:[1,2,3,0,2]
数据约束
见题目描述
输出格式
最大的收益数值
输入样例
[1,2]
[2,1]
[1,2,3,0,2]
[2,3,4,5,6,7]
[1,6,2,7,13,2,8]
输出样例
1
0
3
5
12
解题思路:
问题理解
你需要设计一个算法来计算在给定的股票价格数组中,通过多次买卖股票所能获得的最大利润。这里有两个关键的约束条件:
- 你不能同时参与多笔交易(即在再次购买前必须出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票(即冷冻期为1天)。
数据结构选择
由于我们需要处理的是一个时间序列数据,并且需要考虑冷冻期,动态规划(Dynamic Programming)是一个合适的选择。我们可以使用两个状态数组来记录不同状态下的最大利润:
hold[i]:表示第i天持有股票时的最大利润。sold[i]:表示第i天不持有股票时的最大利润。
算法步骤
-
初始化:
hold[0]初始化为-prices[0],因为第一天买入股票的利润是负的。sold[0]初始化为0,因为第一天不持有股票的利润是0。
-
状态转移:
- 对于每一天
i:hold[i]可以从hold[i-1](前一天持有股票)或者sold[i-2] - prices[i](前两天卖出股票后买入)转移过来。sold[i]可以从sold[i-1](前一天不持有股票)或者hold[i-1] + prices[i](前一天持有股票并卖出)转移过来。
- 对于每一天
-
结果:
- 最终的最大利润是
sold数组中的最大值
- 最终的最大利润是
代码实现:
1.初始化
需要有两个数组,一个存有股票最大利润,一个则是存无股票时的最大利润 ,并对下标0处置0
// 初始化状态数组
std::vector<int> hold(n); // 持有股票的最大利润
std::vector<int> sold(n); // 不持有股票的最大利润
// 初始状态
hold[0] = -stocks[0]; // 第一天买入股票
sold[0] = 0; // 第一天不持有股票2. 进行状态转移:
需要对两种情况(有/无)股票的情况下进行各自的更新
也就是对两个方面进行比较,前者是前一天的利润与当天股票价格的差,后者是当i>=2时,前天的利润,否则为0 与当天股票的价格差。
而不持有股票的数组则是在不持有的前一天与抛售了昨天的股票的利润进行比较
// 状态转移
for (int i = 1; i < n; ++i) {
// 持有股票的状态转移
hold[i] = std::max(hold[i-1], (i >= 2 ? sold[i-2] : 0) - stocks[i]);
// 不持有股票的状态转移
sold[i] = std::max(sold[i-1], hold[i-1] + stocks[i]);
}3.返回: 最终的最大利润是不持有股票的最大利润(一定要卖光)
return sold[n-1];最终代码:
#include <iostream>
#include <vector>
#include <algorithm> // for std::max
int solution(std::vector<int> stocks) {
int n = stocks.size();
if (n == 0) return 0;
// 初始化状态数组
std::vector<int> hold(n); // 持有股票的最大利润
std::vector<int> sold(n); // 不持有股票的最大利润
// 初始状态
hold[0] = -stocks[0]; // 第一天买入股票
sold[0] = 0; // 第一天不持有股票
// 状态转移
for (int i = 1; i < n; ++i) {
// 持有股票的状态转移
hold[i] = std::max(hold[i-1], (i >= 2 ? sold[i-2] : 0) - stocks[i]);
// 不持有股票的状态转移
sold[i] = std::max(sold[i-1], hold[i-1] + stocks[i]);
}
// 最终的最大利润是不持有股票的最大利润
return sold[n-1];
}
int main() {
// 你可以添加更多测试用例
std::cout << (solution({1, 2}) == 1) << std::endl;
std::cout << (solution({2, 1}) == 0) << std::endl;
std::cout << (solution({1, 2, 3, 0, 2}) == 3) << std::endl;
std::cout << (solution({2, 3, 4, 5, 6, 7}) == 5) << std::endl;
std::cout << (solution({1, 6, 2, 7, 13, 2, 8}) == 12) << std::endl;
return 0;
}运行结果: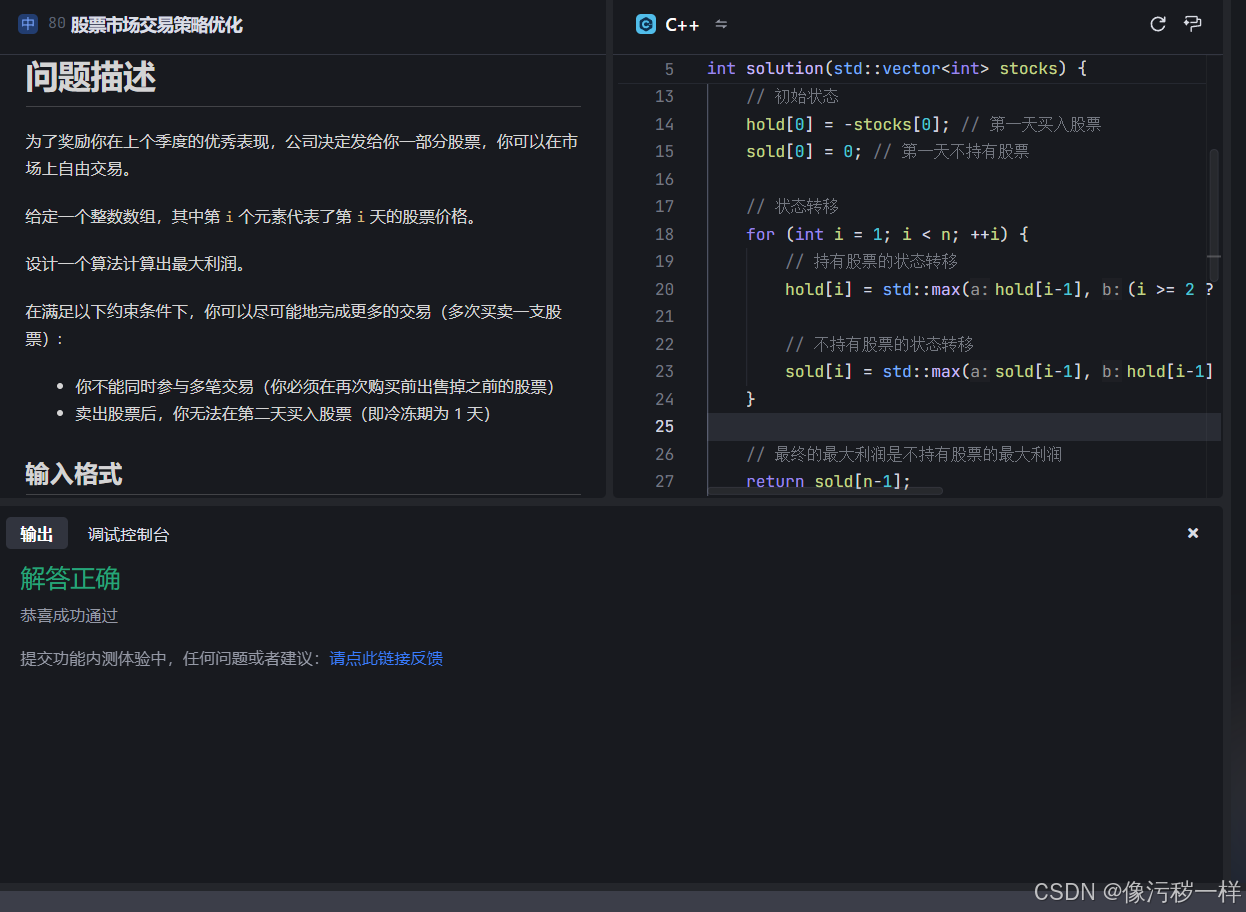


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










