算法分析与设计：动态规划（包含实例）

本文链接：https://blog.youkuaiyun.com/m0_72934718/article/details/139453514

一、实验目的

1、掌握动态规划基本思想，学习动态规划使用动态规划步骤及了解概念；

2、编译一道程序，深入了解动态规划应用思想；

3、总结实验；

二、实验环境

硬件环境:

cpu型号：11th Gen Intel(R) Core(TM) i5-1135G7 @ 2.40GHz

主频内存型号：2.42 GHz

容量：16+512

软件环境:

操作系统版本号：22631.3296

网站：首页 - USCOJ

软件版本：Microsoft Visual Studio 2022

三、实验内容

1、题目描述：购物最大价值

小华是一个精明的购物者，他正在参加一个特别的促销活动。商店里有 N 种

商品，每种商品都有一个价值和一个重量以及限购数量。小华希望在不超过他

的承重限制 W 以及单个商品限购数的情况下，购买尽可能高总价值的商品。

2）输入：

输入共两行，第一行为两个正整数 N 和 W，分别表示商品数量和小华的承重

限制。

接下来有 N 组数据，每组三个整数 wi，vi，si 用空格隔开，分别表示第 i 种

物品的体积、价值和限购数量。

3）输出：

一行，一个整数表示小华可以获得的最大总价值。

4）样例输入：

4 5

2 10 2 1 3 1 4 6 1 2 8 1

5）样例输出

四、实验设计（问题解决方案）

首先在程序中定义一个结构体Item；
使用结构体Item来存储每种商品的重量、价值和限购数量；
定义一个shopping函数，调用此函数来记录数据并统计；
在调用shopping函数中，利用算法动态规划即可求解小华可以获得的最大总价值；
主函数中用CIN使用户输入N、W的值；
通过读取输入数据并调用shopping函数；
最终输出小华可以获得的最大总价值。

五．程序及结果

1、程序代码：

Problem: 1443

User: 20220440137 [22软工04班陈东]

Language: C++

Result: 正确

Time:3 ms

Memory:2176 kb

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;

struct Item {

int weight;

int value;

int limit;

};

int shopping(int N, int W, vector<Item> items) {

vector<int> dp(W + 1, 0);

// 初始化dp数组，表示当前承重下可以获得的最大总价值

for (int i = 0; i < N; i++) {

for (int k = 0; k < items[i].limit; k++) {

// 根据限购数量来遍历

for (int j = W; j >= items[i].weight; j--) {

// 逆序更新dp数组

dp[j] = max(dp[j], dp[j - items[i].weight] + items[i].value);

}

return dp[W];

}

int main() {

int N, W; cin >> N >> W;

vector<Item> items(N);

for (int i = 0; i < N; i++) {

cin >> items[i].weight >> items[i].value >> items[i].limit;

}

int result = shopping(N, W, items);

cout << result << endl; return 0;

}

2、代码截图（VisualStudio2022）

3、用户界面（控制台）：

1）Microsoft Visual Studio 2022

参数

六．实验总结

基本思想：

动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时间无关的静态规划(如线性规划、非线性规划)，只要人为地引进时间因素，把它视为多阶段决策过程，也可以用动态规划方法方便地求解

在这个题目中：小华需要在承重限制和单个商品限购数的条件下购买尽可能高总价值的商品。

1）使用一个结构体Item来表示每种商品的重量、价值和限购数量。

2）定义shopping函数来实现动态规划算法，计算小华可以获得的最大总价值。

3）在主函数中，读取输入数据包括商品数量N、承重限制W以及每种商品的重量、价值和限购数量。

4）调用shopping函数，并输出小华可以获得的最大总价值。

这个题目的关键在于利用动态规划的思想，在受限购数约束的情况下，通过遍历每种商品及其限购数量，动态更新当前承重下可以获得的最大总价值。最终返回小华可以获得的最大总价值。

优点：

能够得到全局最优解；可以得到一族最优解；由于动态规划方法反映了动态过程演变的联系和特征，在计算时可以利用实际知识和经验提高求解效率。

缺点：

没有统一的标准模型；

七、其他实例

1.TSP（旅行商问题）

1）问题描述：旅行商问题即 TSP（Traveling Salesman Problem），又称为货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。描述：旅行商问题即 TSP（Traveling Salesman Problem），又称为货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

2）解决思路：保存的数都是不重复的比较小的整数，所以这里用二进制串表示集合。比如集合{1,3,5,6,7}表示成二进制串用1110101，其中集合里面有的数对应的位数写成1，没有的写成0。要判断第3位是不是1，就把 1110101右移(3-1)位，得到11101，然后结果和00001进行 & 运算，如果结果是1说明第3位是1，否则说明第3位是0。推广一下，对于数字x，要看它的第i位是不是1，那么可以通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现。

3）代码（C++）

4）运行控制台

2.零钱兑换问题（leetcode.cn-N.O322·中等）

1）问题描述：

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例输入输出：

数据要求：

2）解决思路：

定义一个coinChange函数来计算最少的硬币数量。然后在main函数中给定了输入数组和金额，并打印出最小的硬币数量。

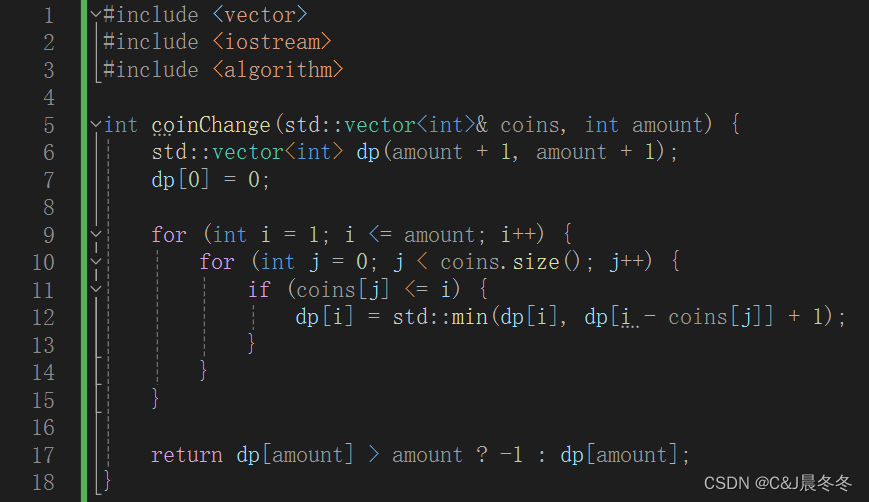
3）代码：（C++，VisualStudio 2022 community Manegement）

4）方案检查：

coins=[1,2,5],amount=11,输出：3；

coins=[2],amount=3,输出：-1；

coins=[1],amount=0;输出：0

coinChange函数首先接收一个整数数组coins和一个整数amount作为参数，分别表示不同面额的硬币和总金额。函数返回一个整数，表示可以凑成总金额所需的最少硬币个数。
在函数内部，首先创建了一个长度为amount + 1的整型向量dp，并初始化所有元素为 amount + 1。dp数组用于存储每个金额需要的最少硬币数量，初始时除了dp[0]为0以外，其余值均设置为无穷大。
使用两层循环遍历金额从1到amount，并尝试每种硬币的组合。
内层循环遍历硬币面额数组coins，对于每个硬币面额coins[j]，如果该硬币面额小于等于当前金额i，则尝试更新dp[i]为dp[i - coins[j]] + 1和当前dp[i]的较小值。
最终返回 dp[amount] 的值，如果它大于 amount 则表示无法凑出总金额，返回 -1，否则返回最小的硬币数量。
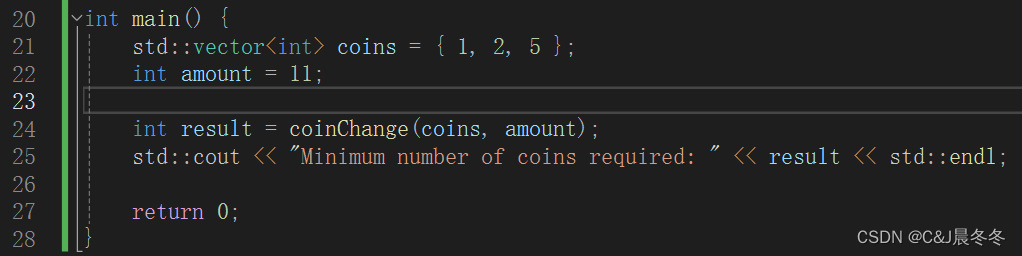
在main函数中，给定了一个示例输入数组{1, 2, 5}和金额11，调用coinChange函数计算最少的硬币数量，并将结果打印输出。