【数据结构与算法】EP1 时间复杂度与空间复杂度

1.算法效率

1.从数学和游戏的角度来谈一下算法效率

算法效率分析分为两种：第一种是时间效率，第二种是空间效率。时间效率被称为时间复杂度，而空间效率 被称作空间复杂度。

时间复杂度主要衡量的是一个算法的运行速度。

比如我们曾经在数学课本上了解过的高斯算法的故事

故事大概是讲高斯上小学时很聪明但也很顽皮，经常在上课时捣乱，某次惹了老师生气后，老师想要教育一下高斯，于是在放学后让他计算1+2+3+....+100的值算完才许他放学。我们如果要用程序来完成，大部分的第一反应应该是写一个循环

int main()
{
    int i = 0, a = 100;
	int sum = 0;
	for (i = 1; i <= a; i++)
	{
	sum += i;
	}
    return 0;
}

然而这样计算的话效率是非常低的。老师的本意是为难一下高斯，但高斯却很快的算了出来。

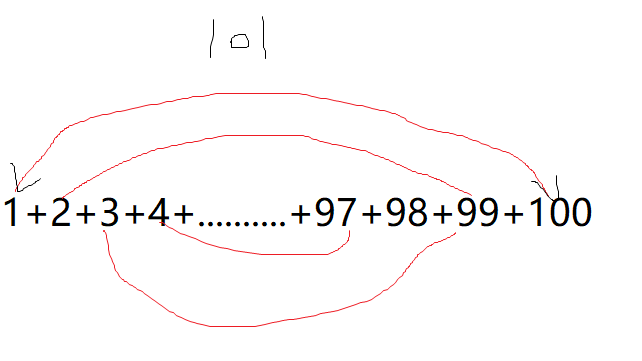
而高斯是怎么算的呢，他首先将1+100，2+99....，50+51我们只需要就算101x50就可以了

int main()
{
	int a = 100;
	int sum =(a / 2) * (1 + a);
	return 0;
}

这样就算我们计算1+到1000的数也只需要计算一步就可以了，是不是很巧妙呢。

而空间复杂度主要衡量一个算法所需要的额外空间。

在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。

比如在游戏的开发过程中能够在内存中完成的事（诸如字体和某些图像的绘制等）就在内存中完成，避免引入外部素材来节约内存和硬盘。

 

不过经过计算机 行业的迅速发展，计算机的存储容量已经达到了很高的程度，很多开发者可以更加肆意的去使用我们的硬盘，我们所玩到的游戏也越来越精致。

因此我们很多时候已经不需要再特别关注一个算法的空间复杂度了。

 讲到这里忽然想到之前看过的一个段子

十年前的程序员：来看看我开发的512kb的宝可梦好不好玩

十年后的程序员：呜呜，我就写了一个"hello word"怎么就1个G了

当然段子只是段子，大家看一乐就好，不需要去纠结内容的严谨性。

对空间复杂度的要求虽然伴随着硬件设备日新月异的变化，但对时间复杂度的追求确是永恒的。

1.时间复杂度

1.什么是时间复杂度

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一 个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知 道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法 的时间复杂度。

单看概念似乎有点难以理解，我们以实例来讲解一下

void Func(int n)
{
	int count = 0;
	for (int i = 0; i < n; i++)
	{
		count++;
	}
}

 在这个函数之中count++在循环中执行了n次，所以它的时间复杂度就是n

void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			count++;
		}
	}
	for (int k = 0; k < 2 * N; k++)
	{
		count++;
	}
	int M = 10;
	while (M--)
	{
		count++;
	}
	printf("%d\n", count);
}

 上面的这段程序count++操作执行了N^2+2*N+10次，它的时间复杂度就是N^2+2*N+10

2.大O的渐进表示法

我们在题目或者课本上看到的时间复杂度说明基本都是使用的大O的渐进表示法

实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这 里我们使用大O的渐进表示法。

我们假设N趋近于无穷大那么，很多项的影响将会接近于没有。我们假设一个程序需要执行的操作数为2*N^2+2*N+10，如果N趋近于无穷大那个2N和10的影响将会越来越小接近于没有。

1、用常数1取代运行时间中的所有加法常数。

2*N^2+2*N+1（如果只有常数项，那么它的时间复杂度就是O(1)）

2、在修改后的运行次数函数中，只保留最高阶项。

2*N^2

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

N^2

所以这个时间复杂度就是O(N^2)

3.空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践 复杂度类似，也使用大O渐进表示法。

void BubbleSort(int* a, int n)
{
 assert(a);
 for (size_t end = n; end > 0; --end)
 {
 int exchange = 0;
 for (size_t i = 1; i < end; ++i)
 {
 if (a[i-1] > a[i])
 {
 Swap(&a[i-1], &a[i]);
 exchange = 1;
 }
 }
 if (exchange == 0)
 break;
 }
}

 这个之中我们使用了常数个额外空间，空间复杂度为O(1)

long long* Fibonacci(size_t n)
{
 if(n==0)
 return NULL;
 
 long long * fibArray =
 (long long *)malloc((n+1) * sizeof(long long));
 fibArray[0] = 0;
 fibArray[1] = 1;for (int i = 2; i <= n ; ++i)
 {
 fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
 }
 return fibArray ;
}

我们动态开辟了n个空间复杂度为O(n)

long long Factorial(size_t N)
{
 return N < 2 ? N : Factorial(N-1)*N;
}

函数在每次调用时都会在栈上开辟空间，这里我们递归了n次，开辟了n个个栈帧所以空间复杂度也是O(N)